菜鳥入門_Python_機器學習(4)_PCA和MDA降維和聚類
@sprt
*寫在開頭:博主在開始學習機器學習和Python之前從未有過任何程式設計經驗,這個系列寫在學習這個領域一個月之後,完全從一個入門級菜鳥的角度記錄我的學習歷程,程式碼未經優化,僅供參考。有錯誤之處歡迎大家指正。
系統:win7-CPU;
程式設計環境:Anaconda2-Python2.7,IDE:pycharm5;
參考書籍:
《Neural Networks and Learning Machines(Third Edition)》- Simon Haykin;
《Machine Learning in Action》- Peter Harrington;
《Building Machine Learning Systems with Python》- Wili Richert;
C站裡都有資源,也有中文譯本。
我很慶幸能跟隨老師從最基礎的東西學起,進入機器學習的世界。*
來看我們這次課的任務:
•資料Cat4D3Groups是4維觀察資料,
•請先採用MDS方法降維到3D,形成Cat3D3Groups資料,顯示並觀察。
•對Cat3D3Groups資料採用線性PCA方法降維到2D,形成Cat2D3Groups資料,顯示並觀察。
•對Cat2D3Groups資料採用K-Mean方法對資料進行分類並最終確定K,顯示分類結果。
•對Cat2D3Groups資料採用Hierarchical分類法對資料進行分類,並顯示分類結果。
理論一旦推導完成,程式碼寫起來就很輕鬆:
Part 1:降維處理
MDA:
# -*- coding:gb2312 -*- PDA:
# -*- coding:gb2312 -*-
from pylab import *
from numpy import *
from mpl_toolkits.mplot3d import Axes3D
def PCA(data, K):
# 資料標準化
m = mean(data, axis=0) # 每列均值
data -= m
# 協方差矩陣
C = cov(transpose(data))
# 計算特徵值特徵向量,按降序排序
evals, evecs = linalg.eig(C)
indices = argsort(evals) # 返回從小到大的索引值
indices = indices[::-1] # 反轉
evals = evals[indices] # 特徵值從大到小排列
evecs = evecs[:, indices] # 排列對應特徵向量
evecs_K_max = evecs[:, :K] # 取最大的前K個特徵值對應的特徵向量
# 產生新的資料矩陣
finaldata = dot(data, evecs_K_max)
return finaldata
# test
'''
data = genfromtxt("CAT4D3GROUPS.txt")
# 4D 轉 3D
data_PCA = PCA(data, 3)
# print data_PCA
figure(1)
ax = subplot(111, projection='3d')
ax.scatter(data_PCA[:, 0], data_PCA[:, 1], data_PCA[:, 2], c='b')
ax.set_zlabel('Z') #座標軸
ax.set_ylabel('Y')
ax.set_xlabel('X')
title('PCA_4to3')
# 4D 轉 2D
data_PCA = PCA(data, 2)
print data_PCA
figure(2)
plot(data_PCA[:, 0], data_PCA[:, 1], 'b.')
xlabel('x')
ylabel('y')
title('PCA_4to2')
'''
程式碼裡的註釋囉囉嗦嗦應該解釋的很清楚,這裡不再贅述,看結果:
1、用MDS方法降維到3D,形成Cat3D3Groups資料:
共兩個函式,輔助函式用來生成歐氏距離矩陣,MDS函式用於降維。
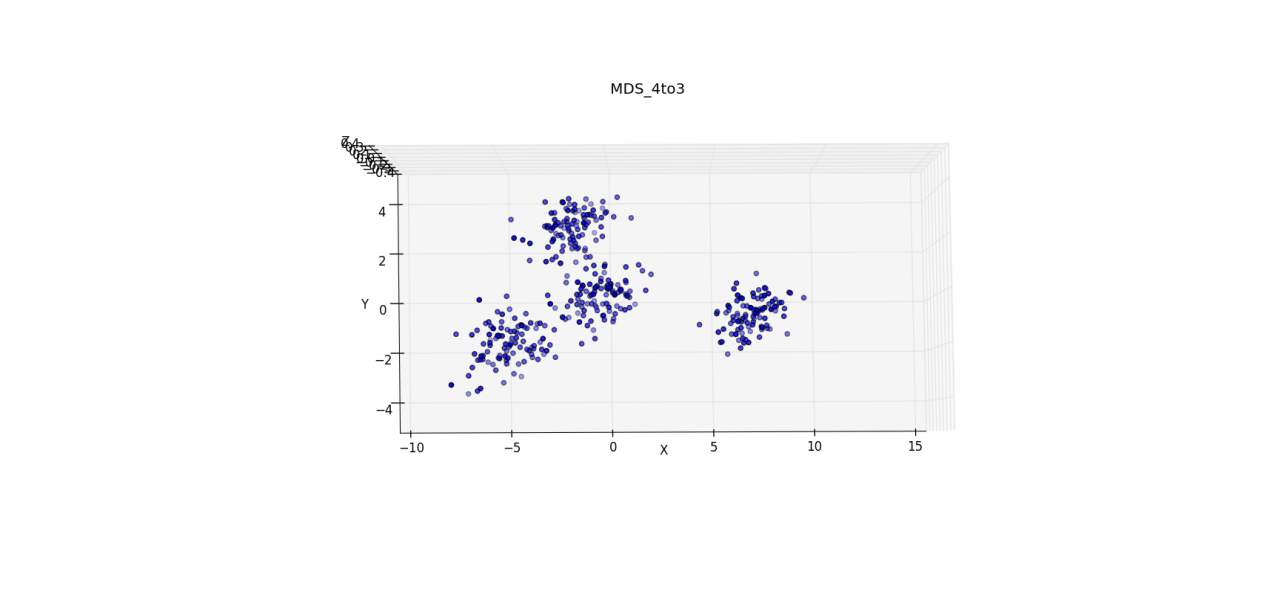

通過輸出的距離矩陣可以看出,降維前後歐氏距離誤差小於10^-4,證明演算法有效。同時旋轉3D影象也可以明顯找出2D平面圖的視角
2、用PCA方法降維到2D,形成Cat2D3Groups資料:
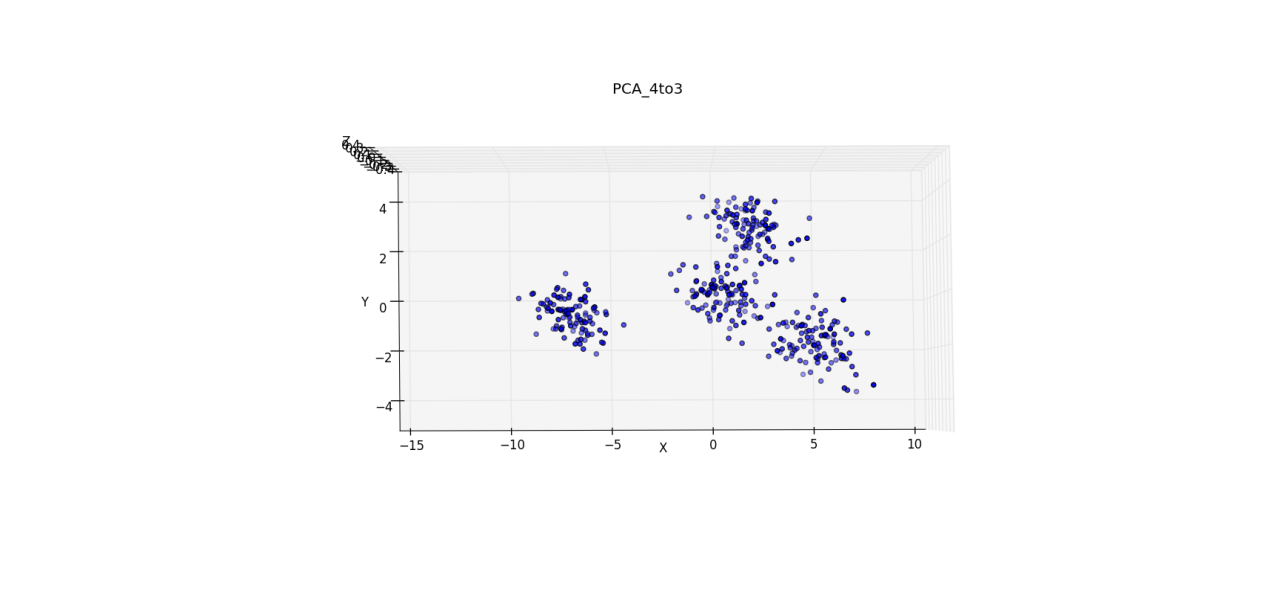
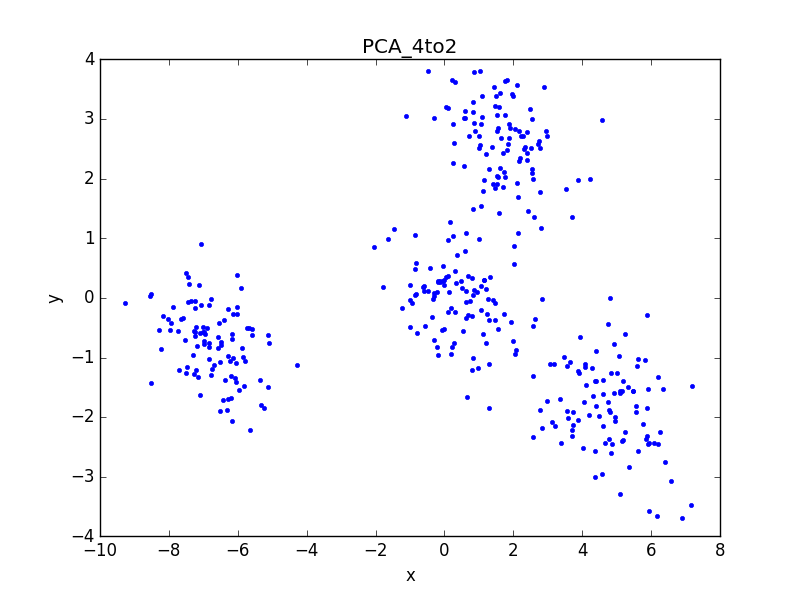
用PCA直接對4D資料降維後的結果與MDS等價,證明演算法有效。同時旋轉3D影象也可以明顯找出2D平面圖的視角。
3、總結分析:
先用MDS演算法將4D資料降到3D,再用PCA降到2D。
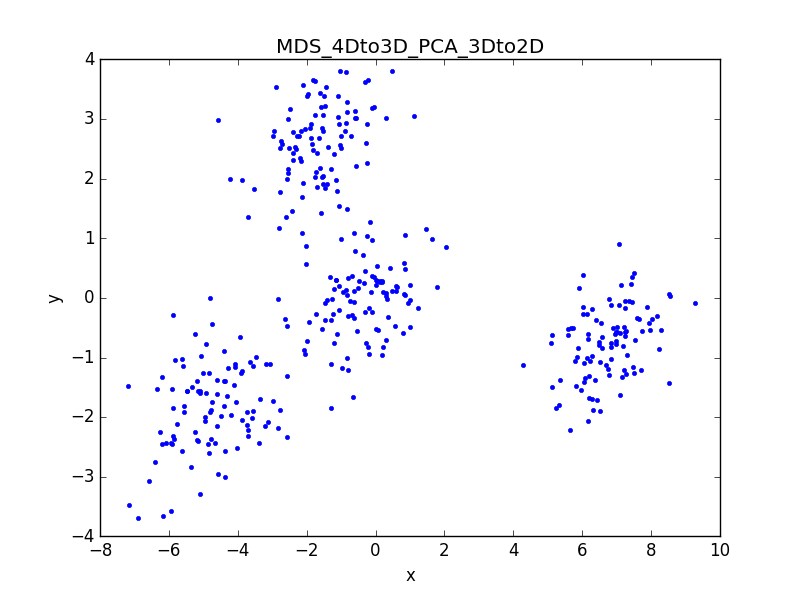
與MDS降維生成的2D影象及資料對比,誤差忽略不計,證明演算法有效,同時證明MDS和PCA演算法在進行小批量資料降維處理上效果類似。
Part 2:聚類分析:
資料用前面降維之後的二維資料。K-means聚類分析的程式主要參考《Machine Learning in Action》- Peter Harrington這本書第十章,我自己添加了選擇最優K值的功能:
# -*- coding:gb2312 -*-
import numpy as np
from pylab import *
from numpy import *
# 求歐氏距離
def euclDistance(vector1, vector2):
return np.sqrt(np.sum(np.power(vector2 - vector1, 2)))
# 返回某個值在列表中的全部索引值
def myfind(x, y):
return [ a for a in range(len(y)) if y[a] == x]
# 初始化聚類點
def initCentroids(data, k):
numSamples, dim = data.shape
centroids = np.zeros((k, dim))
for i in range(k):
index = int(np.random.uniform(0, numSamples))
centroids[i, :] = data[index, :]
return centroids
# K-mean 聚類
def K_mean(data, k):
## step 1: 初始化聚點
centroides = initCentroids(data, k)
numSamples = data.shape[0]
clusterAssment = np.zeros((numSamples, 2)) # 儲存每個樣本點的簇索引值和誤差
clusterChanged = True
while clusterChanged:
clusterChanged = False
global sum
sum = []
# 對每一個樣本點
for i in xrange(numSamples):
minDist = np.inf # 記錄最近距離
minIndex = 0 # 記錄聚點
## step 2: 找到距離最近的聚點
for j in range(k):
distance = euclDistance(centroides[j, :], data[i, :])
if distance < minDist:
minDist = distance
minIndex = j
## step 3: 將該樣本歸到該簇
if clusterAssment[i, 0] != minIndex:
clusterChanged = True # 前後分類相同時停止迴圈
clusterAssment[i, :] = minIndex, minDist ** 2 # 記錄簇索引值和誤差
## step 4: 更新聚點
for j in range(k):
index = myfind(j, clusterAssment[:, 0])
pointsInCluster = data[index, :] # 返回屬於j簇的data中非零樣本的目錄值,並取出樣本
centroides[j, :] = np.mean(pointsInCluster, axis=0) # 求列平均
# 返回cost funktion值
suml = 0
lenght = pointsInCluster.shape[0]
for l in range(lenght):
dis = euclDistance(centroides[j, :], pointsInCluster[l, :])
suml += dis ** 2 / lenght
sum.append(suml)
cost = np.sum(sum) / k
print cost
return centroides, clusterAssment, cost
# 畫出分類前後結果
def showCluster(data, k, centroides, clusterAssment):
numSamples, dim = data.shape
mark = ['r.', 'b.', 'g.', 'k.', '^r', '+r', 'sr', 'dr', '<r', 'pr']
# draw all samples
for i in xrange(numSamples):
markIndex = int(clusterAssment[i, 0])
figure(2)
plt.plot(data[i, 0], data[i, 1], mark[markIndex])
plt.title('K-means')
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']
# draw the centroids
for i in range(k):
figure(2)
plt.plot(centroides[i, 0], centroides[i, 1], mark[i], markersize = 12)
其中三個輔助函式用於求歐氏距離,返回矩陣索引值和畫圖,k-mean函式用於聚類,當所有樣本點到其所屬聚類中心距離不變時,輸出聚類結果,並返回cost function的值。
Cost function計算方法:對每個簇,求所有點到所屬聚類中心的歐氏距離,平方後取均值E。聚類結束後,所有簇E值求和取平均得到cost function的值。
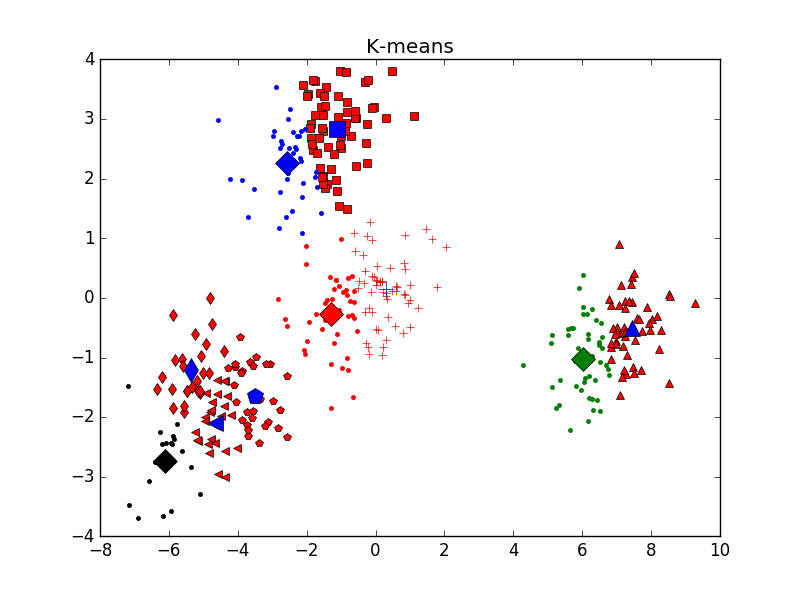
不同K值下的分類結果如下(標明聚類中心):
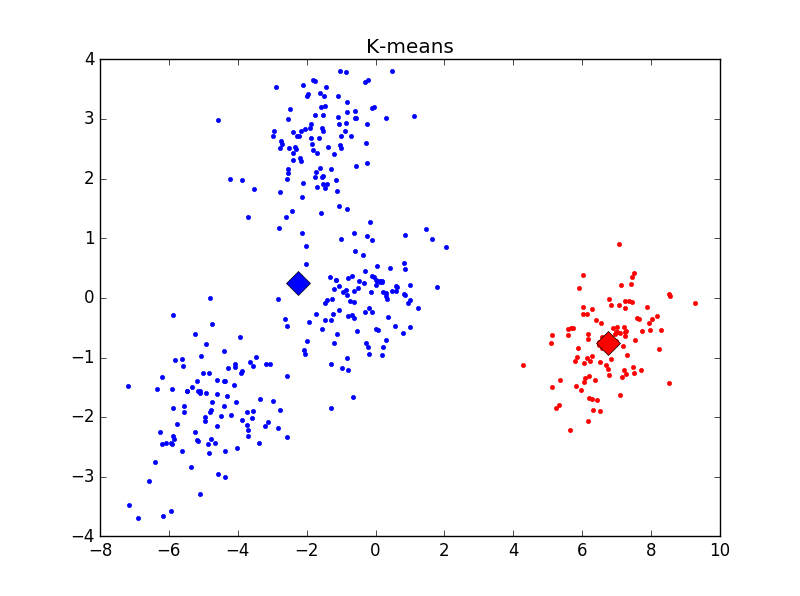
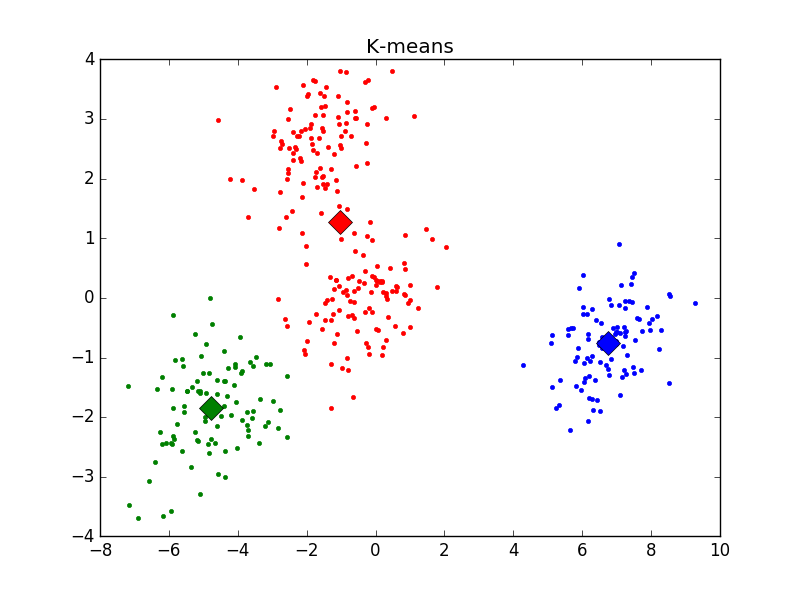
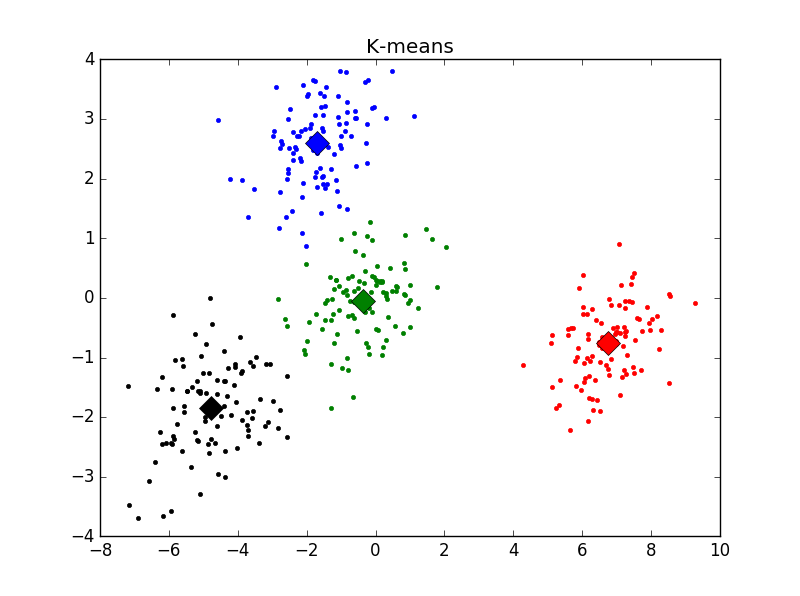

主觀判斷,k = 4時聚類結果最優。用Elbow方法選擇K值結果如下:
發現在K = 2時cost function值下降最為明顯,與之前判斷的結果不符。思考後發現,K=1時聚類沒有意義,所以上圖並不能有效選擇K值,調整後結果如下:

明顯看出,k = 4時cost function下降極為明顯。與主觀判斷結果相符。
Hierarchical分類,參考網上程式碼,出處不記得了:
# -*- coding:gb2312 -*-
import numpy as np
import matplotlib.pyplot as plt
import MDS
import PCA
def yezi(clust):
if clust.left == None and clust.right == None :
return [clust.id]
return yezi(clust.left) + yezi(clust.right)
def Euclidean_distance(vector1,vector2):
length = len(vector1)
TSum = sum([pow((vector1[i] - vector2[i]),2) for i in range(len(vector1))])
SSum = np.sqrt(TSum)
return SSum
def loadDataSet(fileName):
a = []
with open(fileName, 'r') as f:
data = f.readlines() #txt中所有字串讀入data
for line in data:
odom = line.split() #將單個數據分隔開存好
numbers_float = map(float, odom) #轉化為浮點數
a.append(numbers_float) #print numbers_float
a = np.array(a)
return a
class bicluster:
def __init__(self, vec, left=None,right=None,distance=0.0,id=None):
self.left = left
self.right = right #每次聚類都是一對資料,left儲存其中一個數據,right儲存另一個
self.vec = vec #儲存兩個資料聚類後形成新的中心
self.id = id
self.distance = distance
def list_array(wd, clo):
len_=len(wd)
xc=np.zeros([len_, clo])
for i in range(len_):
ad = wd[i]
xc[i, :] = ad
return xc
def hcluster(data, n) :
[row,column] = data.shape
data = list_array(data, column)
biclusters = [bicluster(vec = data[i], id = i) for i in range(len(data))]
distances = {}
flag = None
currentclusted = -1
while(len(biclusters) > n) : #假設聚成n個類
min_val = np.inf #Python的無窮大
biclusters_len = len(biclusters)
for i in range(biclusters_len-1) :
for j in range(i + 1, biclusters_len):
#print biclusters[i].vec
if distances.get((biclusters[i].id,biclusters[j].id)) == None:
#print biclusters[i].vec
distances[(biclusters[i].id,biclusters[j].id)] = Euclidean_distance(biclusters[i].vec,biclusters[j].vec)
d = distances[(biclusters[i].id,biclusters[j].id)]
if d < min_val:
min_val = d
flag = (i,j)
bic1,bic2 = flag #解包bic1 = i , bic2 = j
newvec = [(biclusters[bic1].vec[i] + biclusters[bic2].vec[i])/2 for i in range(len(biclusters[bic1].vec))] #形成新的類中心,平均
newbic = bicluster(newvec, left=biclusters[bic1], right=biclusters[bic2], distance=min_val, id = currentclusted) #二合一
currentclusted -= 1
del biclusters[bic2] #刪除聚成一起的兩個資料,由於這兩個資料要聚成一起
del biclusters[bic1]
biclusters.append(newbic)#補回新聚類中心
clusters = [yezi(biclusters[i]) for i in range(len(biclusters))] #深度優先搜尋葉子節點,用於輸出顯示
return biclusters,clusters
def showCluster(dataSet, k, num_mark):
numSamples, dim = dataSet.shape
mark = ['r.', 'b.', 'g.', 'k.', '^r', '+r', 'sr', 'dr', '<r', 'pr']
# draw all samples
for i in xrange(numSamples):
plt.plot(dataSet[i, 0], dataSet[i, 1], mark[num_mark])
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Hierarchical')
if __name__ == "__main__":
# 載入資料
dataMat =np.genfromtxt('CAT4D3GROUPS.txt') #400*4
dataSet = PCA.PCA(dataMat, 2)
k,l = hcluster(dataSet, 10) # l返回了聚類的索引
# 選取規模最大的k個簇,其他簇歸為噪音點
for j in range(len(l)):
m = []
for ii in range(len(l[j])):
m.append(l[j][ii])
m = np.array(m)
a = dataSet[m]
showCluster(a,len(l),j)
plt.show()
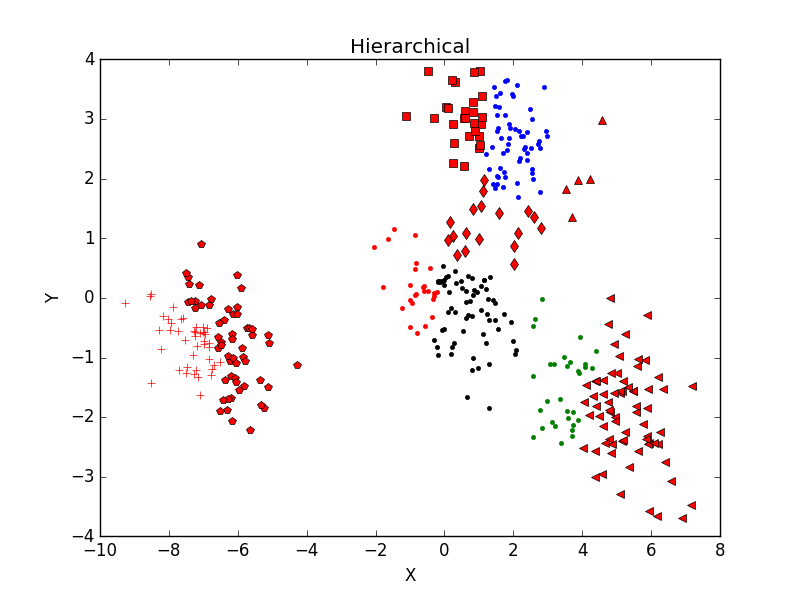
當一個類集合中包含多個樣本點時,類與類之間的距離取Group Average:把兩個集合中的點兩兩的歐氏距離全部放在一起求平均值,分類結果如下:
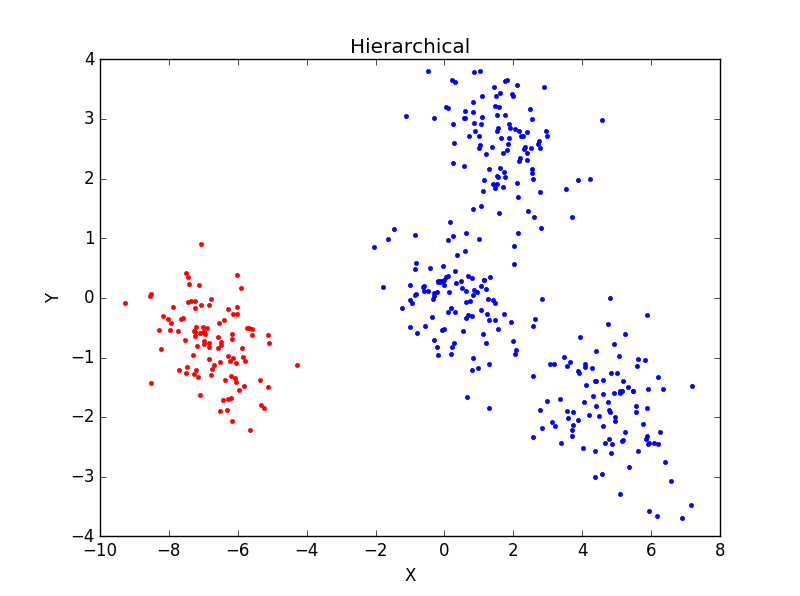

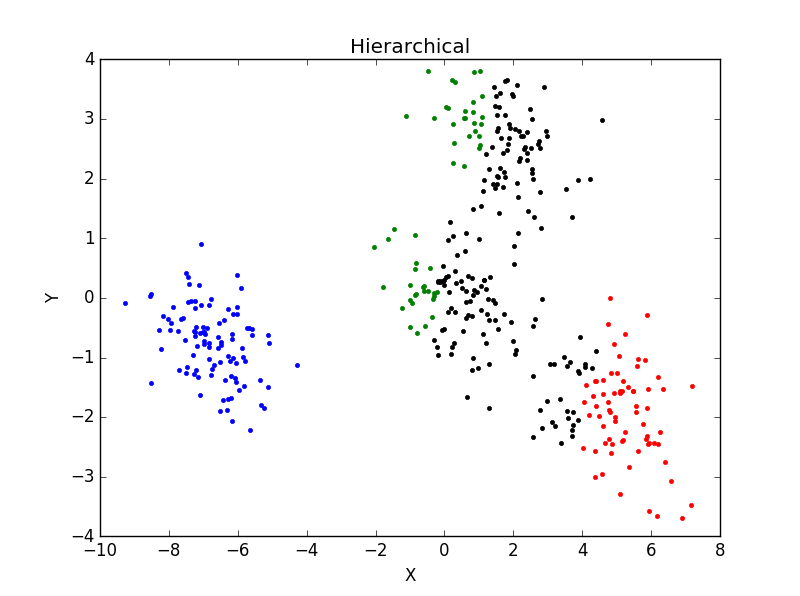
重複執行後分類結果並未有太大變化。主觀判斷,從分成3類及4類的結果看,Hierarchical分類方法效果不如K-mean聚類效果好。
相關推薦
菜鳥入門_Python_機器學習(4)_PCA和MDA降維和聚類
@sprt *寫在開頭:博主在開始學習機器學習和Python之前從未有過任何程式設計經驗,這個系列寫在學習這個領域一個月之後,完全從一個入門級菜鳥的角度記錄我的學習歷程,程式碼未經優化,僅供參考。有錯誤之處歡迎大家指正。 系統:win7-CPU; 程式
菜鳥入門_Python_機器學習(3)_迴歸
@sprt *寫在開頭:博主在開始學習機器學習和Python之前從未有過任何程式設計經驗,這個系列寫在學習這個領域一個月之後,完全從一個入門級菜鳥的角度記錄我的學習歷程,程式碼未經優化,僅供參考。有錯誤之處歡迎大家指正。 系統:win7-CPU; 程式
Python菜鳥快樂遊戲程式設計_pygame(4)
Python菜鳥快樂遊戲程式設計_pygame(博主錄製,2K解析度,超高清) https://study.163.com/course/courseMain.htm?courseId=1006188025&share=2&shareId=400000000398149 為了熟悉鍵盤,
機器學習(4)-多元線性迴歸
一個唯一的因變數和多個自變數 之間的關係 這裡自變數在處理之前不僅僅是數值型 上圖: 我們要做的也就是,尋找到最佳的b0、b1、…….bn 這裡有關於50個公司的資料: spend1、2、3代表了公司在某三個方面的花銷,state是公司的的地址
機器學習(4)K最近鄰演算法
定義:根據最近的樣本決定測試樣本的類別。為了判斷未知例項的類別,以所有已知類別的例項作為參照 選擇引數K 計算未知例項與所有已知例項的距離 選擇最近K個已知例項 根據少數服從多數的投票法則(majority-voting),讓未知例項歸類為K個
機器學習(4):python基礎及fft、svd、股票k線圖、分形等實踐
本節我們主要簡單介紹機器學習常用的語言–python。樓主本身是寫java的,在這之前對python並不瞭解,接觸之後發現python比java簡直要好用幾千倍。這裡主要通過常用的統計量、fft、股票k線圖及分形等樣例,介紹python的使用及各種包的載入。
機器學習(4):資料分析的工具-pandas的使用
前面幾節說一些沉悶的概念,你若看了估計已經心生厭倦,我也是。所以,找到了一個理由來說一個有興趣的話題,就是資料分析。是什麼理由呢?就是,機器學習的處理過程中,資料分析是經常出現的操作。就算機器對大量樣本預測了結果,那對結果進行資料分析與展示,也是經常遇到的標準作業,所以,這一次,來看看怎麼做到資料分析的。 在
機器學習(七)—Adaboost 和 梯度提升樹GBDT
獲得 決策樹 info gin 否則 它的 均方差 但是 ont 1、Adaboost算法原理,優缺點: 理論上任何學習器都可以用於Adaboost.但一般來說,使用最廣泛的Adaboost弱學習器是決策樹和神經網絡。對於決策樹,Adaboost分類用了CART分類樹,
SQL Server AlwaysON從入門到進階(4)——分析和部署Windows Server Failover Cluster
可以看到每個節點已經有一個相同的權重或者票數,但是再看動態節點權重(DynamicWeight列)已經重新平衡。節點4已經動態撤銷投票以便確保投票配置按奇數節點投票。提醒:在Windows 2012 R2中,唯一一個關閉動態節點權重功能的方式只有通過PowerShell實現。意味著微軟並不希望你關閉。現在我們
菜鳥之路——機器學習之HierarchicalClustering層次分析及個人理解
features clu 機器 層次 節點類 均值 成了 range n) 這個算法。我個人感覺有點雞肋。最終的表達也不是特別清楚。 原理很簡單,從所有的樣本中選取Euclidean distance最近的兩個樣本,歸為一類,取其平均值組成一個新樣本,總樣本數少1;不斷的重
Python入門學習(4)
刪除包含特定值得所有列表元素 pets = ['cat','dog','goldfish','cat','rabit','cat'] print(pets) while 'cat' in pets: pets.remove('cat') print(pets)
Linux真小白入門教程第七集——Bash Shell命令學習(4)
之前講了Linux對檔案和目錄的管理和相關操作,下面主要講一些Linux系統管理的一些命令,來探查Linux系統的內部資訊。 Linux系統管理員面臨的最複雜的任務之一就是跟蹤執行在系統中的程式。圖形化介面總是顯示不出所有正在執行的程式,好在還有一些命令可以進行管理。
[學習筆記]菜鳥教程Swift知識點總結(一)
目錄基本語法資料型別變數、常量可選型別字面量運算子 基本語法 Swift 的多行註釋可以巢狀在其他多行註釋內部。寫法是在一個多行註釋塊內插入另一個多行註釋。第二個註釋塊封閉時,後面仍然接著第一個註釋塊
Docker入門學習(4)----Dockerfile製作第一個映象和容器中的第一個javaweb應用
我們可以通過編寫Dockerfile來製作自己的映象,下面先動手來操作一下,製作一個映象,然後基於該映象執行一個容器,在容器裡執行我們自己的javaweb應用。 <1>拉取tomcat映象 docker pull tomcat 檢視映象: roo
機器學習(一):快速入門線性分類器
定義 假設特徵與分類結果存線上性關係的模型,這個模型通過累加計算每個維度的特徵與各自權重的乘積來幫助類別決策。 線性關係公式 :f(w,x,b)=w^tx+b x=(x1,x2,…xn) 代表n維特徵列向量,w=(w1,w2,…wn)代表對應的權
機器學習(二):快速入門SVM分類
定義 SVM便是根據訓練樣本的分佈,搜尋所有可能的線性分類器中最佳的那個。仔細觀察彩圖中的藍線,會發現決定其位置的樣本並不是所有訓練資料,而是其中的兩個空間間隔最小的兩個不同類別的資料點,而我們把這種可以用來真正幫助決策最優線性分類模型的資料點稱為”支
用Python開始機器學習(4:KNN分類演算法) sklearn做KNN演算法 python
http://blog.csdn.net/lsldd/article/details/41357931 1、KNN分類演算法 KNN分類演算法(K-Nearest-Neighbors Classification),又叫K近鄰演算法,是一個概念極其簡單,而分類效果又很優秀的
用Python開始機器學習(4:KNN分類演算法)
1、KNN分類演算法KNN分類演算法(K-Nearest-Neighbors Classification),又叫K近鄰演算法,是一個概念極其簡單,而分類效果又很優秀的分類演算法。他的核心思想就是,要確定測試樣本屬於哪一類,就尋找所有訓練樣本中與該測試樣本“距離”最近的前K個
構建之法學習(4)
控制 重要 protect 運算 包裝 二義性 lin c++ 基類 本周學習的內容是兩人合作 計算機只關心編譯生成的機器碼,你的程序采用哪種縮進風格,變量名有無統一的規範等,與機器碼的執行無關。但是,做一個有商業價值的項目,或者在團隊裏工作,代碼規範相當重要。“代碼規
菜鳥教程之工具使用(五)——JRebel與Windows服務的Tomcat集成
-m end 個人 再見 proc key pre 安裝 target 之前寫過一篇Tomcat借助JRebel支持熱部署的文章——《借助JRebel使Tomcat支持熱部署 》。介紹的是在開發、測試環境中的配置。可是正式的部署環境。我們不會通過命令行來啟動Tomcat,