一、前言

本篇文章主要介紹了CNN網路中卷積層的計算過程，欲詳細瞭解CNN的其它資訊可以參考：技術向：一文讀懂卷積神經網路。

卷積神經網路(CNN)是區域性連線網路。相對於全連線網路其最大的特點就是：區域性連線性和權值共享性。因為對一副影象中的某個畫素p來說，一般離畫素p越近的畫素對其影響也就越大（區域性連線性）；另外，根據自然影象的統計特性，某個區域的權值也可以用於另一個區域(權值共享性)。這裡的權值共享說白了就是卷積核共享，對於一個卷積核將其與給定的影象做卷積就可以提取一種影象的特徵，不同的卷積核可以提取不同的影象特徵。概況的講，卷積層的計算方法就是根據公式

conv=σ(imgM

at∘W+b)(1)conv=\sigma (imgMat\circ W+b) (1)

其中”σ\sigma ”表示啟用函式;”imgMatimgMat”表示灰度影象矩陣; ”WW”表示卷積核;”∘\circ ”表示卷積操作；”bb ”表示偏置值。

二、舉例說明

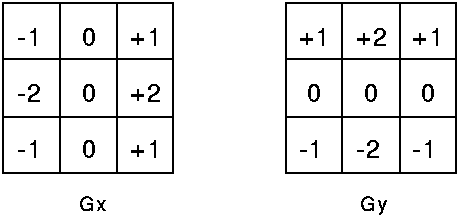
下面用一個具體例子來詳細說明卷積層的計算過程。用到的影象為lena影象，如圖1所示；卷積核為Sobel卷積核，如圖2所示。

圖1 Lena影象(512x512)

圖2 Sobel卷積核(Gx表示水平方向，Gy表示垂直方向)

1、首先用Sobel—Gx卷積核來對影象做卷積，即公式(1)中的imgMat∘WimgMat\circ W

這裡卷積核大小為3x3，影象大小為512x512如果不對影象做任何其它處理，直接進行卷積的話，卷積後的影象大小應該是:(512-3+1)x(512-3+1)。對卷積不懂的可以參考技術向：一文讀懂卷積神經網路或其他讀物。最終結果為：

圖3 lena影象與Sobel—Gx卷積核的卷積結果

2、 將步驟1中所得結果(一個矩陣)的每個元素都加上b(偏置值)，並將所得結果(矩陣)中的每個元素都輸入到啟用函式，這裡取sigmoid函式如下式所示

f(x)=11+e−x(2)f(x)=\frac { 1 }{ 1+{ e }^{ -x } } (2)

最終結果如圖4所示：

圖4 卷積層所得到的最終結果

3、同理，

利用Sobel—Gy卷積核我們最終可以得到如圖5所示的結果。

圖5 Sobel—Gy卷積核卷積層所得到的最終結果

三、完整程式碼及結果

clear
clc
imgRGB = imread('lena.jpg');
imgGray = double(rgb2gray(imgRGB));

Gx = [-1 0 1;-2 0 2;-1 0 1];
convImg = conv2(imgGray,Gx,'valid');
whos convImg
figure
subplot(1,2,1);
imshow(uint8(convImg));
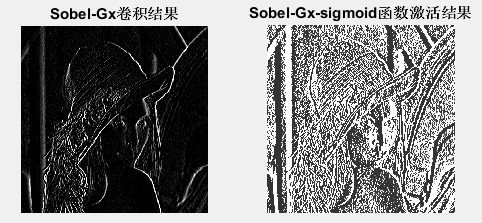
title('Sobel-Gx卷積結果')
b = 0.2;
sigmImg = 1./(1+exp(-convImg)) + b;
subplot(1,2,2);
imshow(sigmImg);
title('Sobel-Gx-sigmoid函式啟用結果')

Gy = [-1 0 1;-2 0 2;-1 0 1]';
convImg = conv2(imgGray,Gy,'valid');
whos convImg
figure
subplot(1,2,1);
imshow(uint8(convImg));
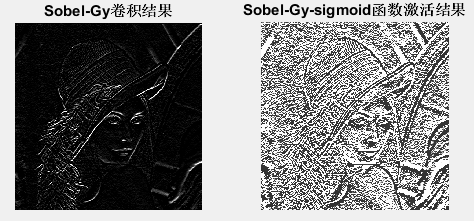
title('Sobel-Gy卷積結果')
b = 0.2;
sigmImg = 1./(1+exp(-convImg)) + b;
subplot(1,2,2);
imshow(sigmImg);
title('Sobel-Gy-sigmoid函式啟用結果')

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30

結果

1、Sobel—Gx卷積核結果

2、Sobel—Gy卷積核結果

四、小結。

以上計算過程，我們只用了兩個卷積核。可以看出兩個卷積核提取出了不同的影象特徵。實際中，我們一般會使用十幾個或者幾十個卷積核來提取影象特徵，進而來進行下一步的運算。