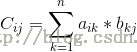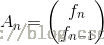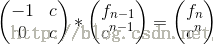矩陣快速冪(總結)
基礎知識:(會基礎的直接看應用部分)
(1)矩陣乘法
簡單的說矩陣就是二維陣列,數存在裡面,矩陣乘法的規則:A*B=C
其中c[i][j]為A的第i行與B的第j列對應乘積的和,即:
程式碼:
const int N=100; int c[N][N]; void multi(int a[][N],int b[][N],int n) { memset(c,0,sizeof c); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) c[i][j]+=a[i][k]*b[k][j]; }
另一種寫法:
int c[N][N];
void multi(int a[][N],int b[][N],int n)
{
memset(c,0,sizeof c);
for(int i=1;i<=n;i++)
for(int k=1;k<=n;k++)
for(int j=1;j<=n;j++)
c[i][j]+=a[i][k]*b[k][j];
}
顯然矩陣乘法的複雜度是O(n^3);(O(n^2.7)的方法不會寫,無視這裡)。
這裡我直接寫的是n*n的矩陣(即方陣),顯然兩個相乘是要一行和一列對應乘,那麼矩陣乘法是需要A的行數與B的列數相等的(這是A*B的前提條件,可見
矩陣的乘法是不滿足交換律的)。然而這些一般都是沒什麼用的,矩陣快速冪只會用到方陣(除非題目是裸的矩陣乘法)。矩陣快速冪都是方陣也就避免的
相乘的前提條件,可以放心用。
(1)矩陣快速冪
就是算A^n;方法很簡單,把快速冪演算法中的乘法改成矩陣的乘法就可以了
程式碼:
這程式碼看看就好,我的寫法一般人不是很喜歡看,網上有很多種寫法,比如用結構體存矩陣什麼的,模板建議還是自己寫的好,自己怎麼寫順溜就怎麼寫唄,弄清楚原理就好。const int N=10; int tmp[N][N]; void multi(int a[][N],int b[][N],int n) { memset(tmp,0,sizeof tmp); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) tmp[i][j]+=a[i][k]*b[k][j]; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) a[i][j]=tmp[i][j]; } int res[N][N]; void Pow(int a[][N],int n) { memset(res,0,sizeof res); for(int i=1;i<=n;i++) res[i][i]=1; while(n) { if(n&1) multi(res,a,n);//res=res*a;複製直接在multi裡面實現了; multi(a,a,n);//a=a*a n>>=1; } }
不過上訴res陣列就等同於普通快速冪初始化的1,原理想通的,這個矩陣叫單位矩陣E,性質就是E*A=A,就是1*a=a,一樣,單位矩陣就是對角線全是1其
他全是0;
最終算出的結果是一個res矩陣,具體有什麼用就看下面的應用。
應用篇
主要通過把數放到矩陣的不同位置,然後把普通遞推式變成"矩陣的等比數列",最後快速冪求解遞推式:
先通過入門的題目來講應用矩陣快速冪的套路(會這題的也可以看一下套路):
例一:http://poj.org/problem?id=3070
題目:斐波那契數列f(n),給一個n,求f(n)%10000,n<=1e9;
(這題是可以用fibo的迴圈節去做的,不過這裡不講,反正是水題)
矩陣快速冪是用來求解遞推式的,所以第一步先要列出遞推式:
f(n)=f(n-1)+f(n-2)
第二步是建立矩陣遞推式,找到轉移矩陣:
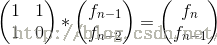
這裡就是個矩陣乘法等式左邊:1*f(n-1)+1*f(n-2)=f(n);1*f(n-1)+0*f(n-2)=f(n-1);
這裡還是說一下構建矩陣遞推的大致套路,一般An與A(n-1)都是按照原始遞推式來構建的,當然可以先猜一個An,主要是利用矩陣乘法湊出矩陣T,第一行一
般就是遞推式,後面的行就是不需要的項就讓與其的相乘係數為0。矩陣T就叫做轉移矩陣(一定要是常數矩陣),它能把A(n-1)轉移到A(n);然後這就是個等
比數列,直接寫出通項:
據自己設定的A(n)對應位置就是對應的值,按照上面矩陣快速冪寫法,res[1][1]=f(n)就是我們要求的。
給一些簡單的遞推式
1.f(n)=a*f(n-1)+b*f(n-2)+c;(a,b,c是常數)
2.f(n)=c^n-f(n-1) ;(c是常數)
Description
Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak.
Input
The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 109) and m (m < 104). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.
Output
Output the elements of S modulo m in the same way as A is given
這題就是求一個矩陣的和式:S(k),直接對和式建立遞推:
建立矩陣,注意此處S和A都是2*2的矩陣,E表示單位矩陣,O表示零矩陣(全是0,與其他矩陣相乘都為0),顯然E,O都是2*2的

一般這種題目都是要找遞推式,這是難點.
題意就是說n個燈排成環i號燈的左邊是i-1號,1的左邊是n號,給定初始燈的開閉狀態(用1,0表示),然後每一秒都操作都是對於每個燈i,如果它左邊的燈
是開的就把i狀態反轉(0變1,1變0),問m秒都最終狀態是什麼,m<=1e8,n<=100;
這題的遞推式沒有明說,但是每一秒操作一次其實就是一次遞推,那麼關鍵就是要找轉移矩陣,而且比較是常數矩陣,這個才能用等比的性質
我們把n個燈的狀態看出一個F(n),其實就是一個n*1的01矩陣,然後考慮從上一秒的狀態F(n-1)如何轉移到F(n)。既然每個狀態都要轉移,總共n個狀態,
可以看出轉移矩陣就是一個n*n的矩陣(每一個燈的狀態都用一個1*n的矩陣來轉移)
先考慮第一個燈:影響它新狀態的只有它左右的燈和它自己的狀態,仔細想一下,1*n的轉移中只有這兩位置有用,那麼其他都是0,就這樣

(這裡不具體講了,只有0,1的狀態,自己列舉一下state1和state2,矩陣相乘後都是能正確轉移的)
其他燈的考慮都是一樣的,最終:

題意就是一個矩陣a,第一行依次是0,233,2333,23333......,給出矩陣的遞推式:a[i][j]=a[i-1][j]+a[i][j-1],輸入的是第零列,求a[n][m],n ≤ 10,m ≤ 109
解:n很小,m很大,m大概就是作為冪次,以每一列為一個矩陣A(n-1)並且向下一列A(n)轉移,那麼關鍵就是找轉移矩陣了:
先看第一行的數233後面每次都添一個3,顯然遞推關係就是A(n-1)*10+3=A(n),這裡多一個3,必須把列數新增一個元素3,也就是一個(n+1)*1的矩陣
A(n).
然後其他的元素轉移會出現一個問題,a[i][j]=a[i-1][j]+a[i][j-1];這裡a[i-1][j]依舊是新一列的元素,這是不能矩陣轉移的,因為矩陣轉移必須從舊的矩陣狀態
A(n-1)變到新狀態A(n)。
那麼這裡a[i-1][j]就用遞迴思想,沿用上一行的轉移矩陣(上一行能轉移出a[i-1][j]),再加上新增的轉移:

當然矩陣還有很多奇葩的遞推,比如這矩陣優化的dp題。
推薦一些題目:
簡單的:
http://acm.hdu.edu.cn/showproblem.php?pid=1757
http://acm.hdu.edu.cn/showproblem.php?pid=1575
不簡單的:
http://acm.hdu.edu.cn/showproblem.php?pid=3483
http://acm.hdu.edu.cn/showproblem.php?pid=2855
http://acm.hdu.edu.cn/showproblem.php?pid=3658
http://acm.hdu.edu.cn/showproblem.php?pid=4565