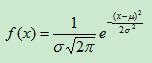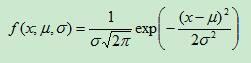正態分佈之python
阿新 • • 發佈:2019-01-09
望為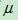 、標準方差為
、標準方差為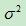 的高斯分佈,記為:
的高斯分佈,記為:
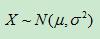
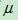 、標準方差為
、標準方差為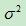 的高斯分佈,記為:
的高斯分佈,記為: 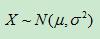
則其概率密度函式為:
正態分佈的期望值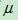
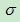
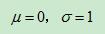
概率密度函式
程式碼實現:
# Python實現正態分佈
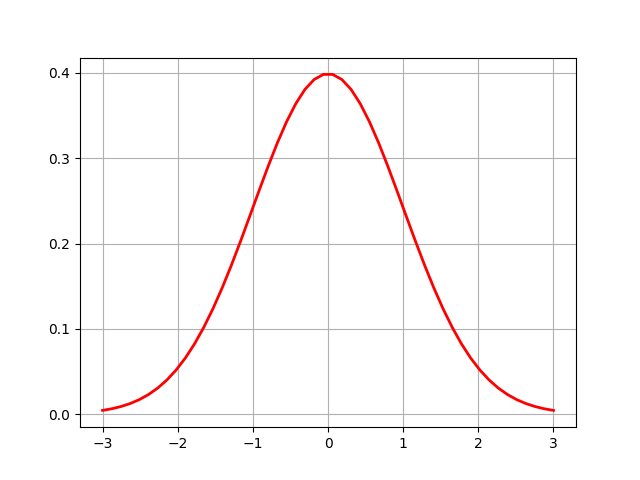
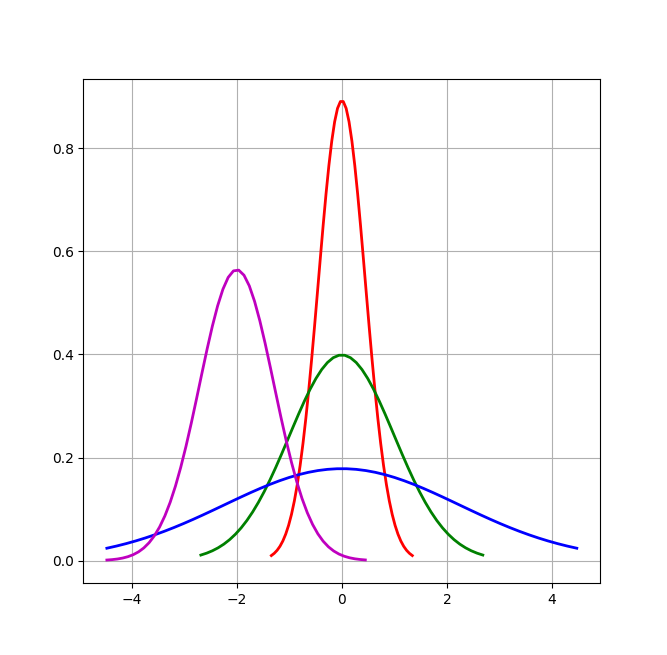
# 繪製正態分佈概率密度函式
u = 0 # 均值μ
u01 = -2
sig = math.sqrt(0.2) # 標準差δ
sig01 = math.sqrt(1)
sig02 = math.sqrt(5)
sig_u01 = math.sqrt(0.5)
x = np.linspace
ps:
期望,意思就是這個事情的總的平均結果會是怎樣
通俗的講,就是平均值,也可以說是平均水平
演算法是
概率*取值的總和,反映的是事情達成的總的預期水平值
這就是期待值
方差是標準差的平方
————————————————
方差和標準差.方差和標準差是測算離散趨勢最重要、最常用的指標.方差是各變數值與其均值離差平方的平均數,它是測算數值型資料離散程度的最重要的方法.標準差為方差的平方根,用S表示.標準差相應的計算公式為
標準差是方差開方後的結果(即方差的算術平方根) 假設這組資料的平均值是m 方差公式s^2=1/n[(x1-m)^2+(x2-m)^2+...+(xn-m)^2]
假設方差是a.則標準差就是這個方差開方
標準差與方差不同的是,標準差和變數的計算單位相同,比方差清楚,因此很多時候我們分析的時候更多的使用的是標準差.