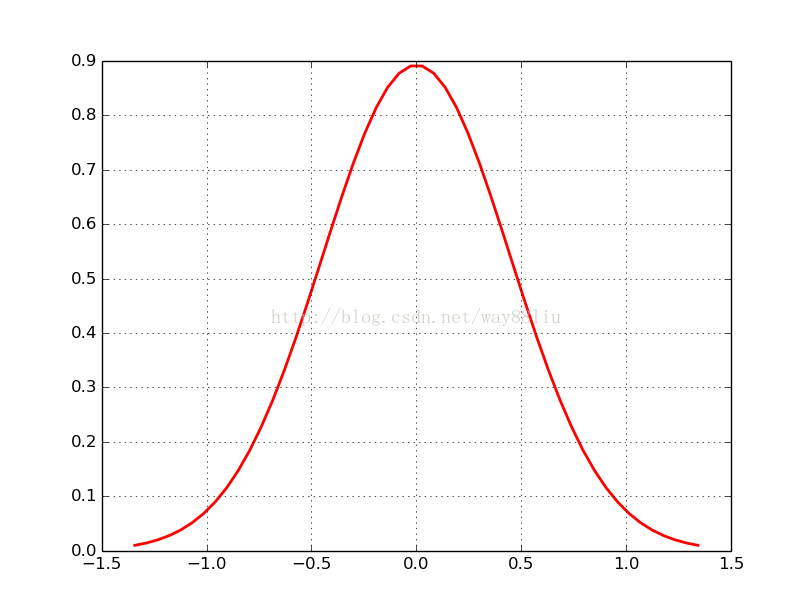
python正態分佈程式碼
程式碼如下:
#-*- coding:utf-8 -*- # Python實現正態分佈 # 繪製正態分佈概率密度函式 import numpy as np import matplotlib.pyplot as plt import math u = 0 # 均值μ u01 = -2 sig = math.sqrt(0.2) # 標準差δ x = np.linspace(u - 3*sig, u + 3*sig, 50) y_sig = np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig) print x print "="*20 print y_sig plt.plot(x, y_sig, "r-", linewidth=2) plt.grid(True) plt.show()
顯示的函式影象如下
相關推薦
python正態分佈程式碼
程式碼如下: #-*- coding:utf-8 -*- # Python實現正態分佈 # 繪製正態分佈概率密度函式 import numpy as np import matplotlib.pyplot as plt import math u = 0 # 均值μ
在python中畫正態分佈/正弦曲線影象/心形線
1 在python中畫正態分佈圖像 import numpy as np import matplotlib.mlab as mlab import matplotlib.pyplot as plt def demo2(): mu, sigma , num_bins = 0,
【114】Python小例子:numpy.random.randn生成符合正態分佈的資料,並畫出正態分佈的鐘曲線。
自己學習python 隨手寫的一個小例子。先利用 numpy.random.randn生成符合正態分佈的資料,然後再給這些資料畫正態分佈的曲線圖。 import numpy as np impor
用Python學分析 - 正態分佈
正態分佈(Normal Distribution) 1、正態分佈是一種連續分佈,其函式可以在實線上的任何地方取值。 2、正態分佈由兩個引數描述:分佈的平均值μ和方差σ2 。 3、正態分佈的取值可以從負無窮到正無窮。 3、Z-score 是非標準正態分佈標準化後的x 即 z = (x−μ) / σ #
python+numpy 隨機數的生成,正態分佈,0-1分佈,均勻分佈及隨機數種子
#! usr/bin/env python # coding: utf-8 # 使用numpy中的隨機函式 學習筆記 # 2018年06月04日11:38:43 北京昌平 import numpy.matlib import numpy as np # 說明,每塊程
正態分佈之python
望為、標準方差為的高斯分佈,記為: 則其概率密度函式為: 正態分佈的期望值決定了其位置,其標準差決定了分佈的幅度。因其曲線呈鐘形,因此人們又經常稱之為鐘形曲線。我們通常所說的標準正態分佈是的正態分佈: 概率密度函式程式碼實現: # Python實現正態分佈 #
安裝spark//python中os.path.abspath及os.path.join以及正態分佈PPF
命令: vim ~/.bashrc source ~/.bashrc ps aux | grep spark pkill -f "spark" sudo chown -R sc:sc spark-2.3.1-bin-hadoop2.7/ sudo mv /ho
python 生成隨機一維或多維正態分佈
作者:採石工 連結:https://www.zhihu.com/question/39823283/answer/115241445 來源:知乎 著作權歸作者所有,轉載請聯絡作者獲得授權。 # coding=utf-8 import numpy as np from
均勻分佈生成標準正態分佈 python
一個分佈的隨機變數可通過把服從(0,1)均勻分佈的隨機變數代入該分佈的反函式的方法得到。均勻分佈的反函式卻求不了。所以我們就要尋找其他的辦法。 由均勻分佈生成標準正態分佈主要有3種方法
從np.random.normal()到正態分佈的擬合
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
截斷正態分佈 Truncated normal distribution
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
正態分佈,銳利分佈,萊斯分佈 matlab擬合原始碼
如果你得到一堆數,你想知道它們的大致分佈,該怎麼辦呢?kedensity命令可以幫助你解決這個問題。命令如下: [f,xi]=ksdensity(x) plot(xi,f) 其中,f是估計的密度值,而xi是一個輔助引數,用來決定畫出圖形的取值區間,簡言之,xi大致涵蓋了x的取值區間。
正態分佈的理解
一、概念 概念:正態分佈,又稱高斯分佈。其特徵為中間高兩邊低左右對稱。 特性: 1)集中性:曲線的最高峰位於正中央,且位置為均數所在的位置。 2)對稱性:正態分佈曲線以均數所在的位置為中心左右對稱且曲線兩段無線趨近於橫軸。 3)均勻變動性:正態分佈曲線以均數所在的位置為中心均勻向左右兩側
課堂練習--計算陣列的最大值,最小值,平均值,標準差,中位數;numpy.random模組提供了產生各種分佈隨機數的陣列;正態分佈;Matplotlib
#計算陣列的最大值,最小值,平均值,標準差,中位數 import numpy as np a=np.array([1, 4, 2, 5, 3, 7, 9, 0]) print(a) a1=np.max(a) #最大值 print(a1) a2=np.min(a) #最小值 print(a2) a3
正態分佈(normal distribution)與偏態分佈(skewed distribution)
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
np.random.rand均勻分佈隨機數和np.random.randn正態分佈隨機數函式使用方法
np.random.rand用法 覺得有用的話,歡迎一起討論相互學習~Follow Me 生成特定形狀下[0,1)下的均勻分佈隨機數 np.random.rand(a1,a2,a3…)生成形狀為(a1,a2,a3…),[0,1)之間的 均勻分佈 隨機數 np
關於使用scipy.stats.lognorm來模擬對數正態分佈的誤區
lognorm方法的引數容易把人搞蒙。例如lognorm.rvs(s, loc=0, scale=1, size=1)中的引數s,loc,scale, 要記住:loc和scale並不是我們通常理解的對數變化後資料的均值mu和標準差sigma,如下面所述: The probability density
黎曼和 Riemann Sum ,黎曼積分Riemann Integral,正態分佈normal distribution
這裡有一塊形狀不規則的土地,要測量它的面積,怎麼辦呢?一個叫黎曼的德國數學家(Bernhard Riemann, 1826-1866),他想了個辦法:將這不規則圖形切成一條條的小長條兒,然後將這個長條近似的看成一個矩形,再分別測量出這些小矩形的長
MATLAB繪製正態分佈概率密度函式(normpdf)圖形
這裡是一個簡單的實現程式碼 x=linspace(-5,5,50); %生成負五到五之間的五十個數,行向量 y=normpdf(x,0,1); plot(x,y,‘k’); 圖片複製不過來。。就擺個連結好了 https://jingyan.baidu.com/article/6fb756ec
均勻分佈差生正態分佈
文章目錄 中心極限定理 中心極限定理 中心極限定理是說,n只要越來越大,這n個數的樣本均值會趨近於正態分佈,並且這個正態分佈以u為均值,sigma^2/n為方差。 換句話說,假設我們與樣本