http://blog.csdn.net/lsldd/article/details/41357931

1、KNN分類演算法

KNN分類演算法（K-Nearest-Neighbors Classification），又叫K近鄰演算法，是一個概念極其簡單，而分類效果又很優秀的分類演算法。

他的核心思想就是，要確定測試樣本屬於哪一類，就尋找所有訓練樣本中與該測試樣本“距離”最近的前K個樣本，然後看這K個樣本大部分屬於哪一類，那麼就認為這個測試樣本也屬於哪一類。簡單的說就是讓最相似的K個樣本來投票決定。

這裡所說的距離，一般最常用的就是多維空間的歐式距離。這裡的維度指特徵維度，即樣本有幾個特徵就屬於幾維。

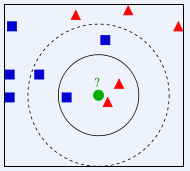
上圖中要確定測試樣本綠色屬於藍色還是紅色。

顯然，當K=3時，將以1：2的投票結果分類於紅色；而K=5時，將以3：2的投票結果分類於藍色。

KNN演算法簡單有效，但沒有優化的暴力法效率容易達到瓶頸。如樣本個數為N，特徵維度為D的時候，該演算法時間複雜度呈O（DN)增長。

所以通常KNN的實現會把訓練資料構建成K-D Tree（K-dimensional tree），構建過程很快，甚至不用計算D維歐氏距離，而搜尋速度高達O（D*log（N））。

不過當D維度過高，會產生所謂的”維度災難“，最終效率會降低到與暴力法一樣。

因此通常D>20以後，最好使用更高效率的Ball-Tree，其時間複雜度為O（D*log（N））。

人們經過長期的實踐發現KNN演算法雖然簡單，但能處理大規模的資料分類，尤其適用於樣本分類邊界不規則的情況。最重要的是該演算法是很多高階

當然，KNN演算法也存在一切問題。比如如果訓練資料大部分都屬於某一類，投票演算法就有很大問題了。這時候就需要考慮設計每個投票者票的權重了。

2、測試資料

測試資料的格式仍然和前面使用的身高體重資料一致。不過資料增加了一些：

1. 1.5 40 thin  
2. 1.5 50 fat  
3. 1.5 60 fat  
4. 1.6 40 thin  
5. 1.6 50 thin  
6. 1.6 60 fat  
7. 1.6 70 fat  
8. 1.7 50 thin  
9. 1.7 60 thin  
10. 1.7 70 fat  
11. 1.7 80 fat  
12. 1.8 60 thin  
13. 1.8 70 thin  
14. 1.8 80 fat  
15. 1.8 90 fat  
16. 1.9 80 thin  
17. 1.9 90 fat  

3、Python程式碼

scikit-learn提供了優秀的KNN演算法支援。使用Python程式碼如下：

1. # -*- coding: utf-8 -*-
2. import numpy as np  
3. from sklearn import neighbors  
4. from sklearn.metrics import precision_recall_curve  
5. from sklearn.metrics import classification_report  
6. from sklearn.cross_validation import train_test_split  
7. import matplotlib.pyplot as plt  
8. ''''' 資料讀入 '''
9. data   = []  
10. labels = []  
11. with open("data\\1.txt") as ifile:  
12.         for line in ifile:  
13.             tokens = line.strip().split(' ')  
14.             data.append([float(tk) for tk in tokens[:-1]])  
15.             labels.append(tokens[-1])  
16. x = np.array(data)  
17. labels = np.array(labels)  
18. y = np.zeros(labels.shape)  
19. ''''' 標籤轉換為0/1 '''
20. y[labels=='fat']=1
21. ''''' 拆分訓練資料與測試資料 '''
22. x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2)  
23. ''''' 建立網格以方便繪製 '''
24. h = .01
25. x_min, x_max = x[:, 0].min() - 0.1, x[:, 0].max() + 0.1
26. y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
27. xx, yy = np.meshgrid(np.arange(x_min, x_max, h),  
28.                      np.arange(y_min, y_max, h))  
29. ''''' 訓練KNN分類器 '''
30. clf = neighbors.KNeighborsClassifier(algorithm='kd_tree')  
31. clf.fit(x_train, y_train)  
32. '''''測試結果的列印'''
33. answer = clf.predict(x)  
34. print(x)  
35. print(answer)  
36. print(y)  
37. print(np.mean( answer == y))  
38. '''''準確率與召回率'''
39. precision, recall, thresholds = precision_recall_curve(y_train, clf.predict(x_train))  
40. answer = clf.predict_proba(x)[:,1]  
41. print(classification_report(y, answer, target_names = ['thin', 'fat']))  
42. ''''' 將整個測試空間的分類結果用不同顏色區分開'''
43. answer = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:,1]  
44. z = answer.reshape(xx.shape)  
45. plt.contourf(xx, yy, z, cmap=plt.cm.Paired, alpha=0.8)  
46. ''''' 繪製訓練樣本 '''
47. plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, cmap=plt.cm.Paired)  
48. plt.xlabel(u'身高')  
49. plt.ylabel(u'體重')  
50. plt.show()  

4、結果分析

其輸出結果如下：

[ 0.  0.  1.  0.  0.  1.  1.  0.  0.  1.  1.  0.  0.  1.  1.  0.  1.]
[ 0.  1.  1.  0.  0.  1.  1.  0.  0.  1.  1.  0.  0.  1.  1.  0.  1.]
準確率=0.94, score=0.94
             precision    recall  f1-score   support
       thin      0.89      1.00      0.94         8
        fat       1.00      0.89      0.94         9
avg / total       0.95      0.94      0.94        17

2、注意統計準確率時，分類器的score返回的是計算正確的比例，而不是R2。R2一般應用於迴歸問題。

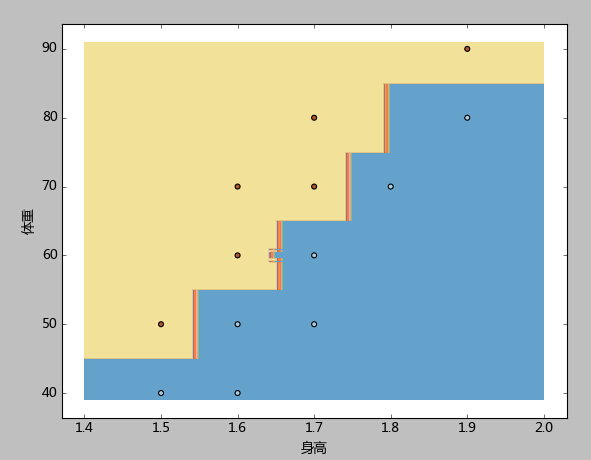
3、本例先根據樣本中身高體重的最大最小值，生成了一個密集網格（步長h=0.01），然後將網格中的每一個點都當成測試樣本去測試，最後使用contourf函式，使用不同的顏色標註出了胖、廋兩類。

容易看到，本例的分類邊界，屬於相對複雜，但卻又與距離呈現明顯規則的鋸齒形。

這種邊界線性函式是難以處理的。而KNN演算法處理此類邊界問題具有天生的優勢。我們在後續的系列中會看到，這個資料集達到準確率=0.94算是很優秀的結果了。

頂

3

踩

0