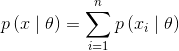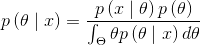接上一篇文章：最大似估計

貝葉斯估計：    引數估計   是最隨機變數，根據觀測資料對引數的分佈進行估計，還要考慮先驗分佈

最大似然估計：  引數估計  是未知的，根據觀測資料來估計  的值。

貝葉斯學習是把貝葉斯估計的原理應用於直接從資料對概率密度進行估計

開始我們今天的表演

一、貝葉斯估計

可以將概率密度函式引數估計問題看成是貝葉斯決策問題

           貝葉斯決策問題有兩類：（1）輸入為離散變數：（用於分類）最優條件可以是最小錯誤率或者是最小風險    

                                                  （2）輸入為連續變數

在使用損失函式為最小平方誤差損失函式的情況下，貝葉斯估計的步驟是：

（1）根據對問題的認識或者猜測確定的先驗分佈密度p();

（2）樣本獨立同分布，且已知樣本密度形式，可以形式上求出樣本集的聯合分佈  

（3）利用貝葉斯公式求的後驗概率分佈

（4）求貝葉斯的估計量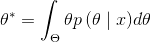        

注：

        我們本來的目的並不是要估計概率密度引數，而是估計樣本的概率密度函式 （小x為樣本，大X為樣本集），就是所有可能的引數取值下的樣本概率密度的加權平均，而這個加權就是在觀測樣本下估計出的引數的後驗概率。那麼決定分佈形式的就是後驗概率的分子的形式（分母的目的就是歸一化，保證密度函式下的積分為1）。分子有兩項，似然函式：反映在不同引數取值下觀測的樣本的可能性。先驗概率：反映對引數分佈的先驗知識或主觀猜測。

        一般情況下，似然函式會在其極大值  附近有一個尖峰，那麼如果先驗概率在最大似然估計處不為零且變化比較平緩，則引數的後驗概率  就會集中在   附近。此時貝葉斯估計就與最大似然估計接近。

二、正態分佈的貝葉斯

為什麼選擇正態分佈？因為 為正態分佈時先驗分佈密度p()也為正態分佈。       

注：對於給定的概率密度函式模型，如果先驗概率密度p()能夠使引數的後驗分佈具有與 相同的形式，則這樣的先驗密度函式形式稱作與概率模型共軛。     

公式。。。（好吧，我又懶了）

注：若遇到求積分不容易的情況，請查閱吉布斯取樣。  

題外話：概率密度估計的非引數方法

       最大似然方法和貝葉斯方法都屬於引數化的估計方法,要求待估計的概率密度函式形式已知,只是利用樣本來估計函式中的某些引數。但是,在很多情況下,我們對樣本的分佈並沒有充分的瞭解,無法事先給出密度函式的形式,而且有些樣本分佈的情況也很難用簡單的函式來描述。在這種情況下,就需要非引數估計,即不對概率度函式的形式作任何假設,而是直接用樣本估計出整個函式。當然,這種估計只能用數值方法取得,無法得到完美的封閉函式形式。從另外的角度來看,概率密度函式的引數估計實際是在指定的一類函式中選擇一個函式作為對未知函式的估計,而非引數估計則可以看作是從所有可能的函式中進行的一種選擇。

1、直方圖方法

2、k近鄰估計法

3、parzen窗法