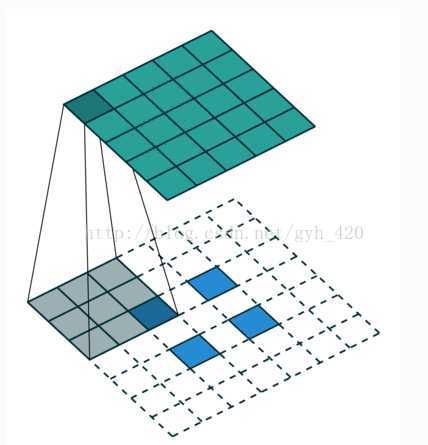
對FCN及反捲積的理解
----主要參考
https://github.com/vdumoulin/conv_arithmetic
https://www.zhihu.com/question/43609045
http://blog.csdn.net/fate_fjh/article/details/52882134
先介紹一波反捲積
1.前言
傳統的CNN網路只能給出影象的LABLE,但是在很多情況下需要對識別的物體進行分割實現end to end,然後FCN出現了,給物體分割提供了一個非常重要的解決思路,其核心就是卷積與反捲積,所以這裡就詳細解釋卷積與反捲積。 對於1維的卷積,公式(離散)與計算過程(連續)如下,要記住的是其中一個函式(原函式或者卷積函式)在卷積前要翻轉180度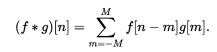
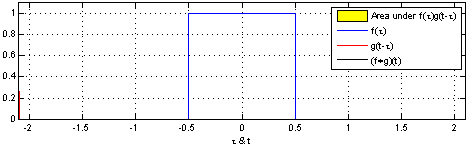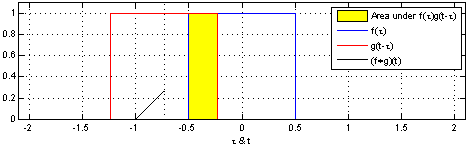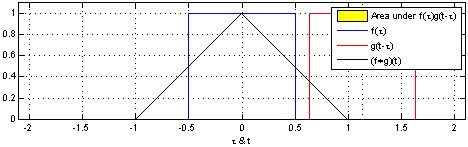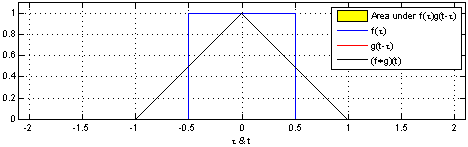
圖1 對於離散卷積,f的大小是n1,g的大小是n2,卷積後的大小是n1+n2-1
2.影象卷積
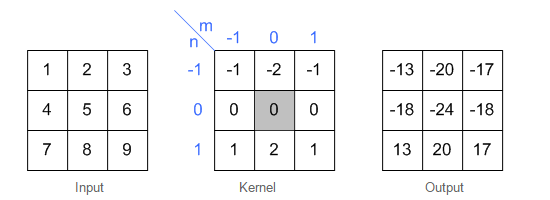
圖2 同樣地,卷積的時候需要對卷積核進行180的旋轉,同時卷積核中心與需計算的影象畫素對齊,輸出結構為中心對齊畫素的一個新的畫素值,計算例子如下

圖3 這樣計算出左上角(即第一行第一列)畫素的卷積後像素值。 給出一個更直觀的例子,從左到右看,原畫素經過卷積由1變成-8。
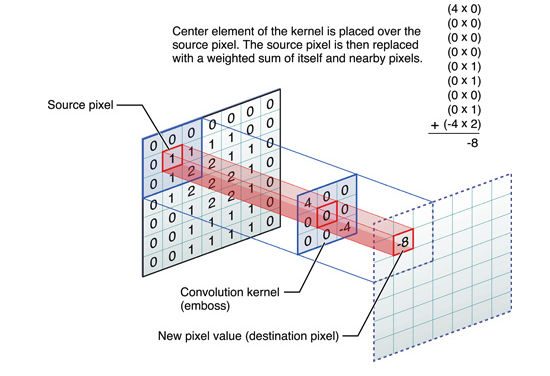
圖4 通過滑動卷積核,就可以得到整張圖片的卷積結果,
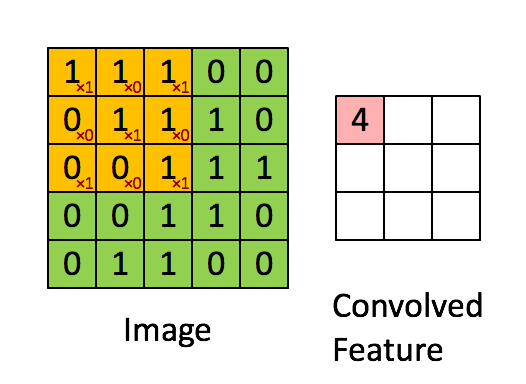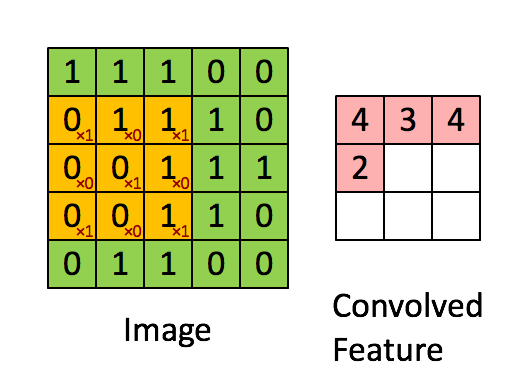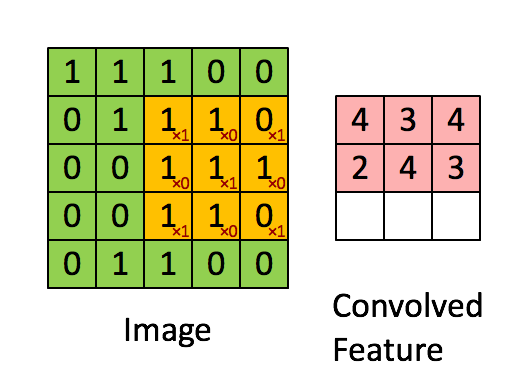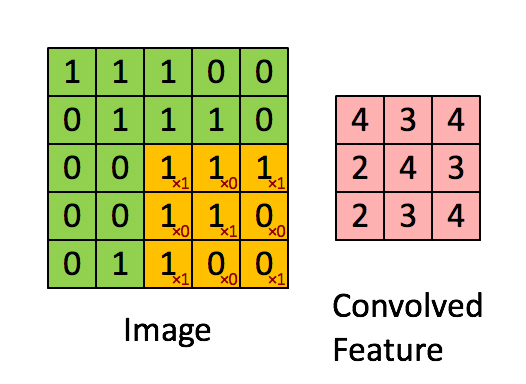
圖5 到了這裡,大致可以明白影象卷積。但是我們可以看出,通過影象卷積後,新影象的大小跟原來一樣,或者變小。圖2計算後圖像大小不變,如圖5卷積後圖像變小是因為沒有對所用畫素進行卷積計算。但是1維的卷積結果不是變大了嗎? 下面對其解釋。 在matlb中對2維卷積的計算分為了3類,1.full 2.same 3. valid 參考:https://cn.mathworks.com/help/matlab/ref/conv2.html?requestedDomain=www.mathworks.com 圖2對應的卷積就是就是所謂的same,圖5對應的就是valid。那麼full又是什麼呢?如下圖
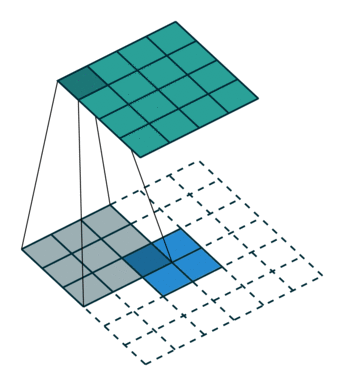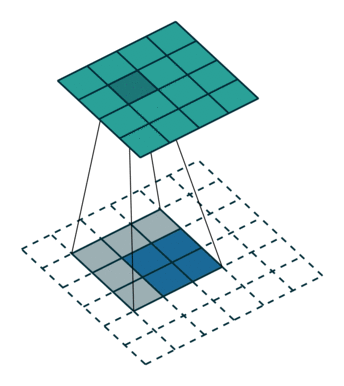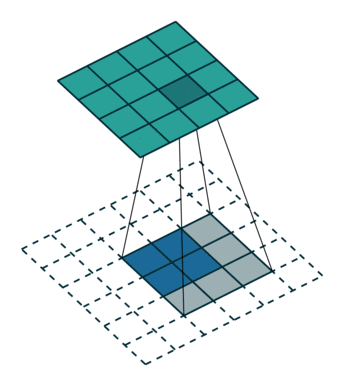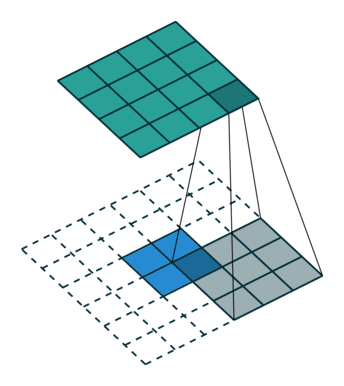
圖6
圖6中藍色為原影象,白色為對應卷積所增加的padding,通常全部為0,綠色是卷積後圖片。圖6的卷積的滑動是從卷積核右下角與圖片左上角重疊開始進行卷積,滑動步長為1,卷積核的中心元素對應卷積後圖像的畫素點。可以看到卷積後的影象是4X4,比原圖2X2大了,我們還記1維卷積大小是n1+n2-1,這裡原圖是2X2,卷積核3X3,卷積後結果是4X4,與一維完全對應起來了。其實這才是完整的卷積計算,其他比它小的卷積結果都是省去了部分畫素的卷積。下面是WIKI對應影象卷積後多出部分的解釋:
Kernel convolution usually requires values from pixels outside of the image boundaries. There are a variety of methods for handling image edges.
3.反捲積(後卷積,轉置卷積)
這裡提到的反捲積跟1維訊號處理的反捲積計算是很不一樣的,FCN作者稱為backwards convolution,有人稱Deconvolution layer is a very unfortunate name and should rather be called a transposed convolutional layer. 我們可以知道,在CNN中有con layer與pool layer,con layer進行對影象卷積提取特徵,pool layer對影象縮小一半篩選重要特徵,對於經典的影象識別CNN網路,如IMAGENET,最後輸出結果是1X1X1000,1000是類別種類,1x1得到的是。FCN作者,或者後來對end to end研究的人員,就是對最終1x1的結果使用反捲積(事實上FCN作者最後的輸出不是1X1,是圖片大小的32分之一,但不影響反捲積的使用)。 這裡影象的反捲積與圖6的full卷積原理是一樣的,使用了這一種反捲積手段使得影象可以變大,FCN作者使用的方法是這裡所說反捲積的一種變體,這樣就可以獲得相應的畫素值,影象可以實現end to end。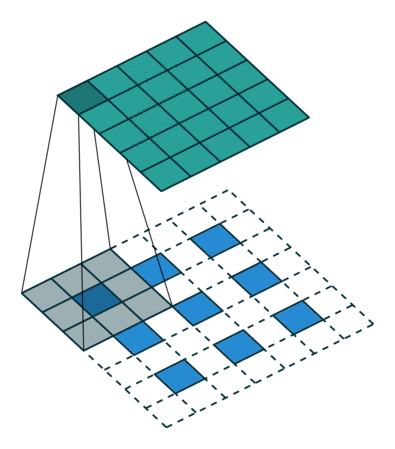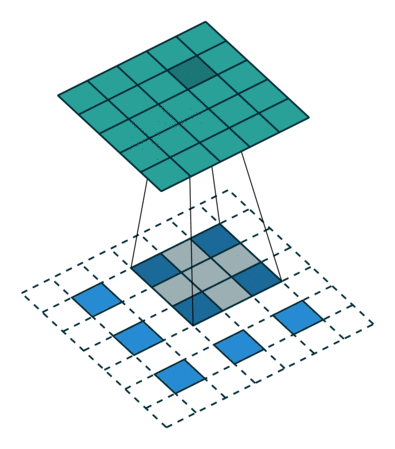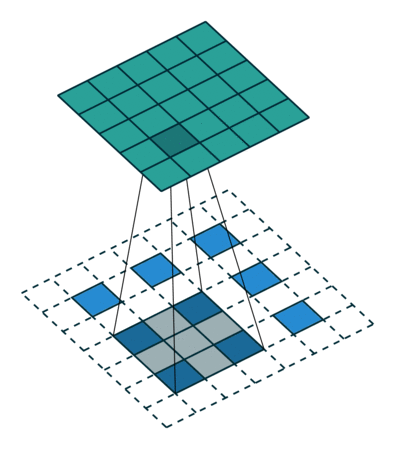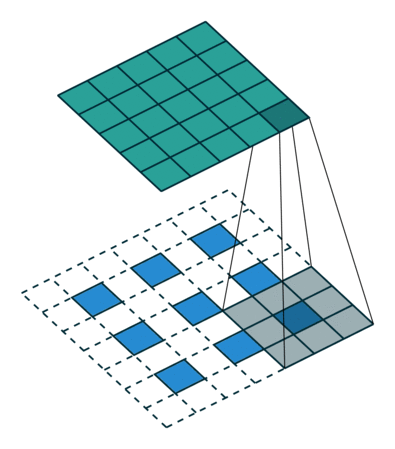
圖7 這裡說另外一種反捲積做法,假設原圖是3X3,首先使用上取樣讓影象變成7X7,可以看到影象多了很多空白的畫素點。使用一個3X3的卷積核對影象進行滑動步長為1的valid卷積,得到一個5X5的影象,我們知道的是使用上取樣擴大圖片,使用反捲積填充影象內容,使得影象內容變得豐富,這也是CNN輸出end to end結果的一種方法。韓國作者Hyeonwoo Noh使用VGG16層CNN網路後面加上對稱的16層反捲積與上取樣網路實現end to end 輸出,其不同層上取樣與反捲積變化效果如下,
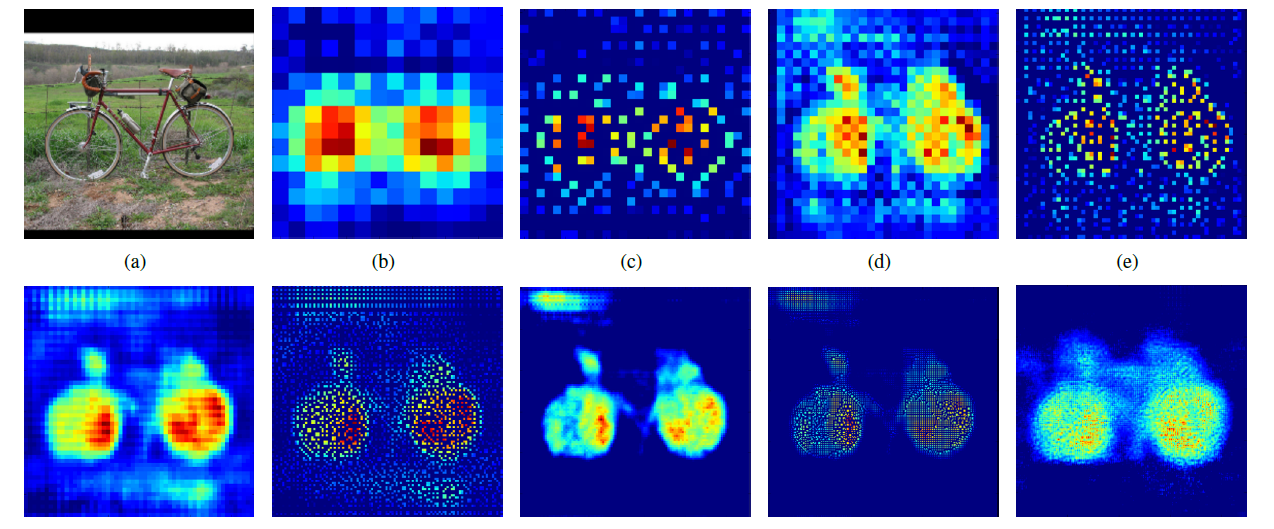
圖8 到這裡就把影象卷積與反捲積解釋完成,如有不妥,請學者們指證。
補充一個資料:
圖6與圖7出處,https://github.com/vdumoulin/conv_arithmetic
經過上面的解釋與推導,對卷積有基本的瞭解,但是在影象上的deconvolution究竟是怎麼一回事,可能還是不能夠很好的理解,因此這裡再對這個過程解釋一下。
目前使用得最多的deconvolution有2種,上文都已經介紹。
方法1:full卷積, 完整的卷積可以使得原來的定義域變大
方法2:記錄pooling index,然後擴大空間,再用卷積填充
影象的deconvolution過程如下,
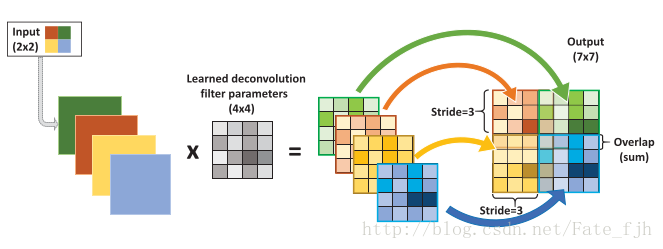
輸入:2x2, 卷積核:4x4, 滑動步長:3, 輸出:7x7
即輸入為2x2的圖片經過4x4的卷積核進行步長為3的反捲積的過程
1.輸入圖片每個畫素進行一次full卷積,根據full卷積大小計算可以知道每個畫素的卷積後大小為 1+4-1=4, 即4x4大小的特徵圖,輸入有4個畫素所以4個4x4的特徵圖
2.將4個特徵圖進行步長為3的fusion(即相加); 例如紅色的特徵圖仍然是在原來輸入位置(左上角),綠色還是在原來的位置(右上角),步長為3是指每隔3個畫素進行fusion,重疊部分進行相加,即輸出的第1行第4列是由紅色特陣圖的第一行第四列與綠色特徵圖的第一行第一列相加得到,其他如此類推。
可以看出翻卷積的大小是由卷積核大小與滑動步長決定, in是輸入大小, k是卷積核大小, s是滑動步長, out是輸出大小
得到 out = (in - 1) * s + k
上圖過程就是, (2 - 1) * 3 + 4 = 7
這裡的步長也可以這樣理解 當stride =1 時,如下的左圖,當stride=2時,如下的右圖
---------------------------------------------------------------------------------------------------------------
參考FCN論文:Fully Convolutional Networks for Semantic Segmentation
FCN作為影象語義分割的先河,實現畫素級別的分類(即end to end,pixel-wise),為後續使用CNN作為基礎的影象語義分割模型提供重要基礎。作者在閱讀FCN論文時,遇到不少困難,同時FCN沒有多少中文資料(更多是英語翻譯),所以作者儘量用淺白的方式講述FCN的原理與過程。
FCN中的CNN
首先回顧CNN測試圖片類別的過程,如下圖 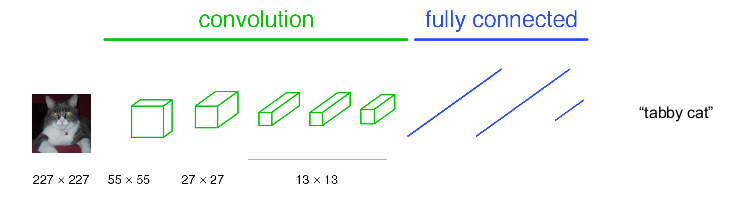
主要由卷積,pool與全連線構成,這裡把卷積與pool都看作圖中綠色的convolution,全連線為圖中藍色的fully connected。卷積主要是獲取高維特徵,pool使圖片縮小一半,全連線與傳統神經網路相似作為權值訓練,最後通過softmax輸出概率最高的類別。上圖中nxn表示feature map(特徵圖)大小, 如原圖大小為227x227,經過卷積與pool後得到55x55的特徵圖(一層的特徵圖可以有多個類別)。注意,不同的卷積操作可能會對圖片大小產生影響,而pool永遠使圖片縮小1/2。–可以參考作者的卷積神經網路CNN(1)。經過多次卷積後特徵圖大小為13x13,特徵圖的權值展開為1維與後面的權值實現全連線,最後使用softmax輸出類別。這就是CNN的大致網路結構與分類過程。
經過CNN改造的FCN如下圖, 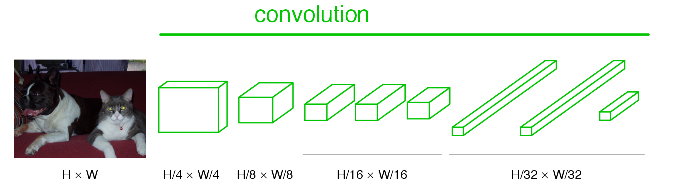
看可以看到藍色的全連線層全部換成卷積層,對於CNN的過程就是做了這麼簡單直白的變換,全卷積的名字由此而來,這就是FCN。圖中nxn是表示特徵圖的大小,可以看到最後特徵圖的大小為原圖的1/32(這與FCN論文中解釋upsample實現end to end 的32stride,16stride,8stride有莫大的關係)。
FCN的upsample
upsample意思為上取樣,簡單來說就是pooling的逆過程,所以pooling也就是下采樣,取樣後資料數量減少,upsample取樣後資料數量增多。FCN作者在論文中討論了3種upsample方法,最後選用的是反捲積的方法(FCN作者稱其為後卷積)使影象實現end to end,可以理解upsample就是使大小比原影象小得多的特徵圖變大,使其大小為原影象大小。 
下面解釋FCN中是如何實現upsample,FCN作者分為FCN-32s,FCN-16s,FCN-8s三種,論文中有一個圖是描述這個三個過程的,如下圖, 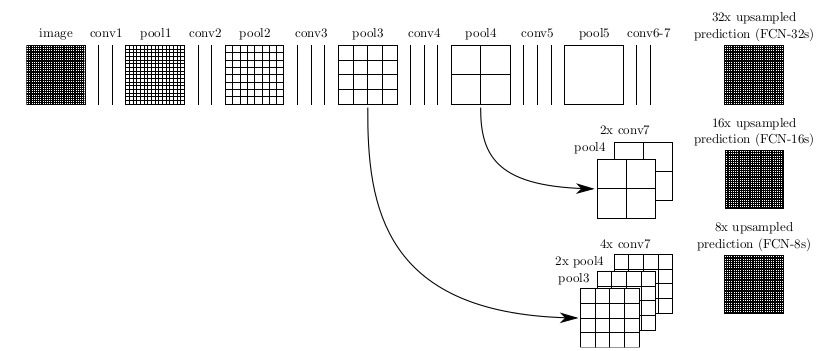
image是原影象,conv1,conv2..,conv5為卷積操作,pool1,pool2,..pool5為pool操作(pool就是使得圖片變為原圖的1/2),注意con6-7是最後的卷積層,最右邊一列是upsample後的end to end結果。必須說明的是圖中nx是指對應的特徵圖上取樣n倍(即變大n倍),並不是指有n個特徵圖,如32x upsampled 中的32x是影象只變大32倍,不是有32個上取樣影象,又如2x conv7是指conv7的特徵圖變大2倍。
第一行對應FCN-32s,第二行對應FCN-16s,第三行對應FCN-8s。
先從FCN-32s開始說明upsample過程,只需要留意第一行,網路裡面有5個pool,所以conv7的特徵圖是原始影象1/32,可以發現最左邊image的是32x32,同時我們知道在FCN中的卷積是不會改變影象大小(或者只有少量畫素的減少,特徵圖大小基本不會小很多),看到pool1是16x16,pool2是8x8,pool3是4x4,pool4是2x2,pool5是1x1,所以conv7對應特徵圖大小為1x1,然後再經過32x upsampled prediction 圖片變回32x32。FCN作者在這裡增加一個卷積層,卷積後的大小為輸入影象的32(2^5)倍,我們簡單假設這個卷積核大小也為32,這樣就是需要通過反饋訓練32x32個權重變數即可讓影象實現end
to end,完成了一個32s的upsample,FCN作者稱做後卷積,他也提及可以稱為反捲積。事實上在原始碼中卷積核的大小為64,同時沒有偏置bias。還有一點就是FCN論文中最後結果都是21x…,這裡的21是指FCN使用的資料集分類,總共有21類。
現在我們把1,2兩行一起看,忽略32x upsampled prediction,說明FCN-16s的upsample過程,,FCN作者在conv7先進行一個2x conv7操作,其實這裡也只是增加1個卷積層,這次卷積後特徵圖的大小為conv7的2倍,可以從pool5與2x conv7中看出來,此時2x conv7與pool4的大小是一樣的,FCN作者提出對pool4與2x conv7進行一個fuse操作(事實上就是將pool4與2x conv7相加),fuse結果進行16x
upsampled prediction,與FCN-32s一樣,也是增加一個卷積層,卷積後的大小為輸入影象的16(2^4)倍,我們知道pool4的大小是2x2,放大16倍,就是32x32,這樣最後影象大小也變為原來的大小,至此完成了一個16s的upsample。現在我們可以知道,FCN中的upsample實際是通過增加捲積層,通過bp反饋的訓練方法訓練卷積層達到end to end,這時卷積層的作用可以看作是pool的逆過程。
這是我們看第1行與第3行,忽略32x upsampled prediction,conv7經過一次4x upsample,即使用一個卷積層,特徵圖輸出大小為conv7的4倍,所以4x conv7的大小為4x4,然後pool4需要一次2x upsample,變成2x pool4,大小也為4x4,最後吧4x conv7,2x pool4與pool3進行fuse,得到求和後的特徵圖,最後增加一個卷積層,使得輸出圖片大小為pool3的8倍,也就是8x upsampled prediction的過程,最後也得到一個end
to end的影象。同時FCN-8s均優於FCN-16s,FCN-32s。
我們可以發現,如果繼續仿照FCN作者的步驟,我們可以對pool2,pool1實現同樣的方法,可以有FCN-4s,FCN-2s,最後得到end to end的輸出。這裡作者給出了明確的結論,超過FCN-8s之後,結果並不能繼續優化。
Fina l l y
結合上述的FCN的全卷積與upsample,在upsample最後加上softmax,就可以對不同類別的大小概率進行估計,實現end to end,最後輸出的圖是一個概率估計,對應畫素點的值越大,其畫素為該類的結果也越大。FCN的核心貢獻在於提出使用卷積層通過學習讓圖片實現end to end分類。事實上,FCN有一些短處,例如使用了較淺層的特徵,因為fuse操作會加上較上層的pool特徵值,導致高維特徵不能很好得以使用,同時也因為使用較上層的pool特徵值,導致FCN對影象大小變化有所要求,如果測試集的影象遠大於或小於訓練集的影象,FCN的效果就會變差。但是,也由於FCN提出了一種新的語義分割的方法,才使得有後面韓國Hyeonwoo Noh的對稱反捲積網路,劍橋的SegNet等優秀用於語義分割的CNN網路。