FCN於反捲積(Deconvolution)、上取樣(UpSampling)
最近在研究影象分割方面的內容,影象分割是對影象進行畫素進行分類。在這裡提到分類,首先想到了 使用深度學習的方法進行分類操作的。
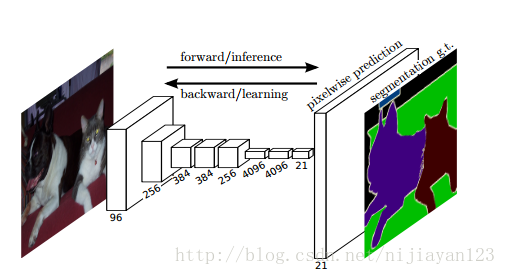
在這裡以前的一些傳統的方法進行的操作,這裡就不細說了。這樣使用了深度學習的方法,提到使用深度學習的方法進行影象分割的話。必須要提到 Fully Convolutional Networks for Semantic Segmentation。這篇文章。這也算是深度學習在影象分割上的首次成功的應用了。這篇文章中使用了遷移學習的概念,這個的Full convolutional 不是傳統神經網路中的全連線網路的意思。這裡表示把原來卷積神經網路的後面的全連線部分換成了反捲積的意思。
在上圖中相比於傳統進行分類的卷積神經網路可以看出把後面的全連線和softmax分類操作的部分 去掉了。換成了後面的分割圖了。
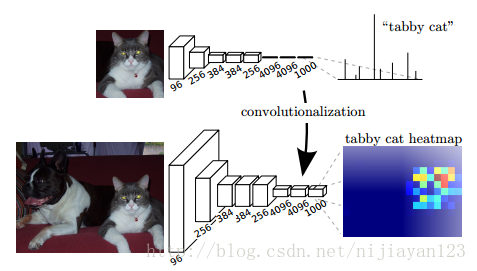
在傳統的CNN結構中,前5層是卷積層,第6層和第7層分別是一個長度為4096的一維向量,第8層是長度為1000的一維向量,分別對應1000個類別的概率。FCN將這3層表示為卷積層,卷積核的大小(通道數,寬,高)分別為(4096,1,1)、(4096,1,1)、(1000,1,1)。所有的層都是卷積層,故稱為全卷積網路。
這篇文章主要的思想就是這個。現在這裡有兩個問題了把卷積神經網路後面的全連線層去掉以後進行反捲積操作,這個具體怎操作,這個反捲積和卷積具體什麼關係。
反捲積
其實說這個問題之前先說一下卷積操作。
卷積操作其實可以分成三種操作,
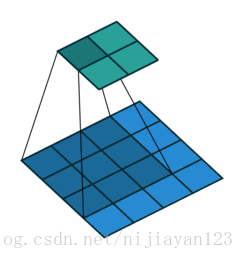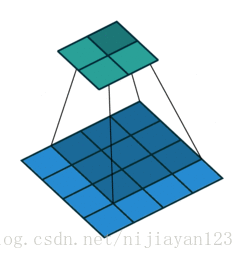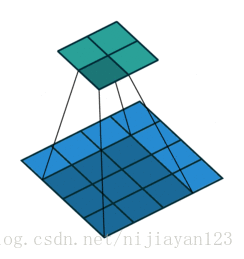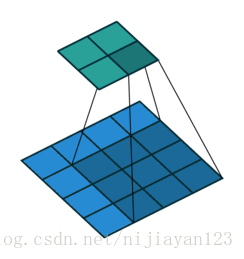
valid 操作,滑動步長為S,圖片大小為N1xN1,卷積核大小為N2xN2,卷積後圖像大小:(N1-N2)/S+1 x (N1-N2)/S+1如下圖
full 操作,滑動步長為1,圖片大小為N1xN1,卷積核大小為N2xN2,卷積後圖像大小:N1+N2-1 x N1+N2-1 如下圖
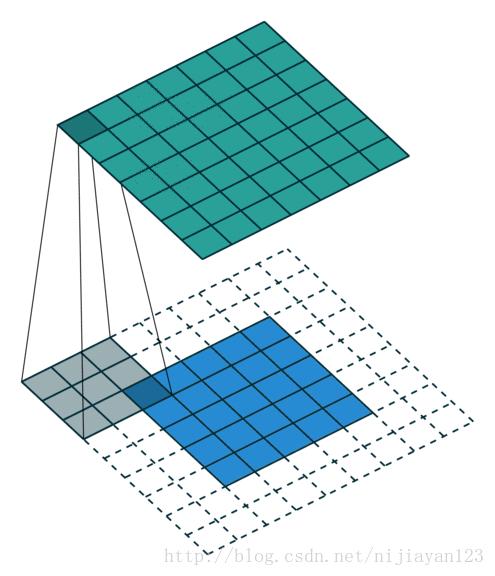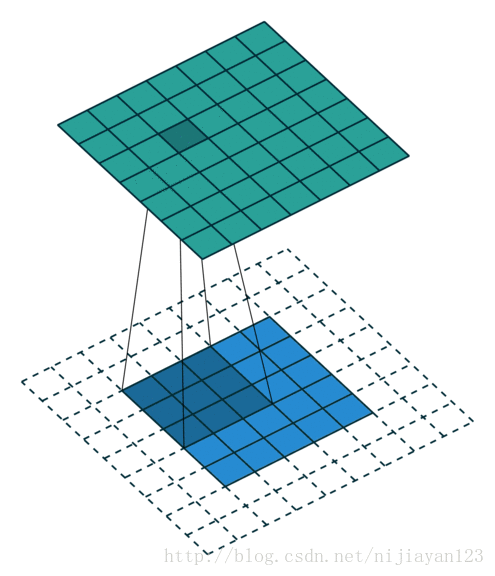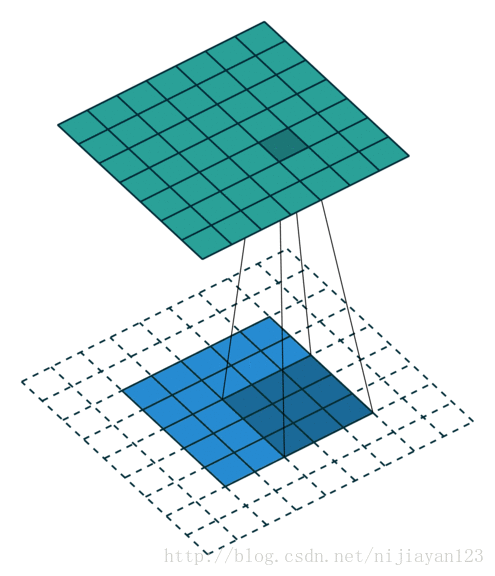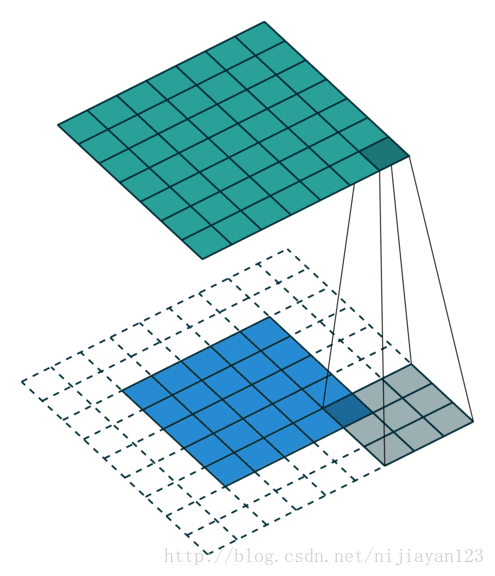
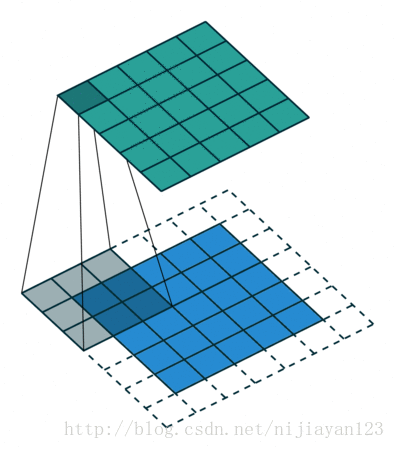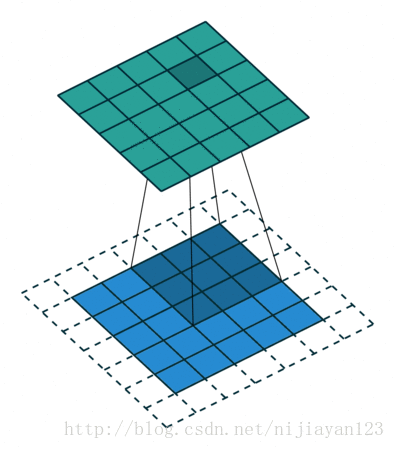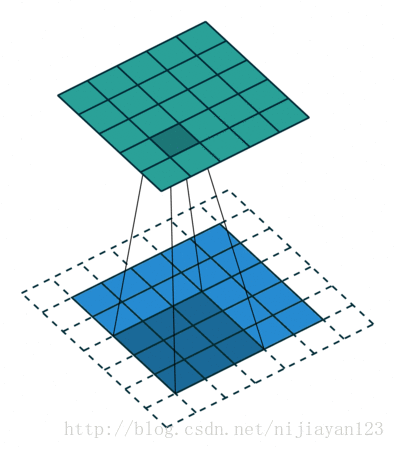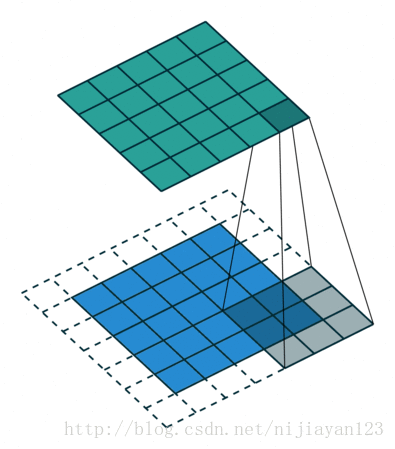
same 操作,滑動步長為1,圖片大小為N1xN1,卷積核大小為N2xN2,卷積後圖像大小:N1xN1 如下圖所示
這是卷積的三種操作,在這篇論文中反捲積也可以稱為上取樣操作,因為相比於下采樣,圖片越來越小的操作,上取樣操作使得整個整個圖片越來越大的操作,
下面看反捲積具體是怎麼操作的
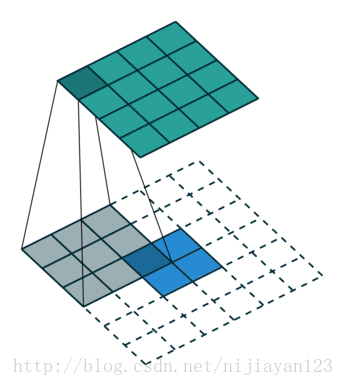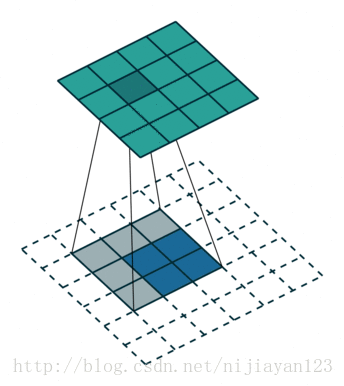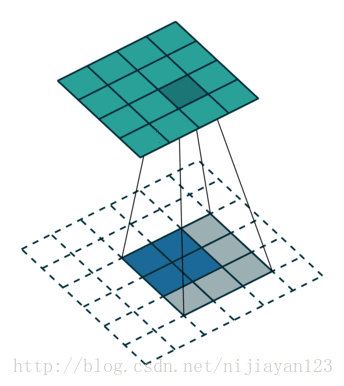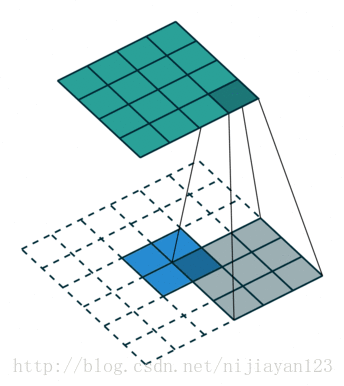
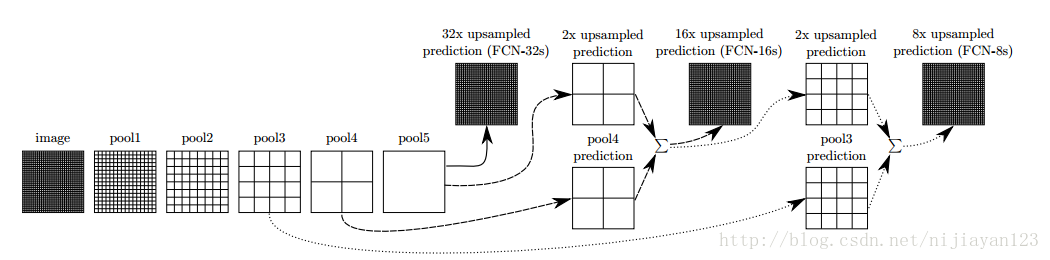
其實這種也算一種卷積的操作,只不過進行了補位操作。在論文中FCN使用了上取樣。例如經過5次卷積(和pooling)以後,影象的解析度依次縮小了2,4,8,16,32倍。對於最後一層的輸出影象,需要進行32倍的上取樣,以得到原圖一樣的大小。這個上取樣是通過反捲積(deconvolution)實現的。對第5層的輸出(32倍放大)反捲積到原圖大小,得到的結果還是不夠精確,一些細節無法恢復。於是Jonathan將第4層的輸出和第3層的輸出也依次反捲積,分別需要16倍和8倍上取樣,結果就精細一些了。下圖是這個卷積和反捲積上取樣的過程:
在這裡論文中使用了另外一種上取樣的方式,它先進行了上池化操作,然後進行了整個卷積操作。整個操作如下圖
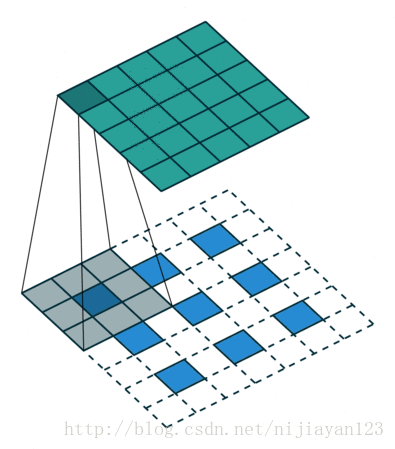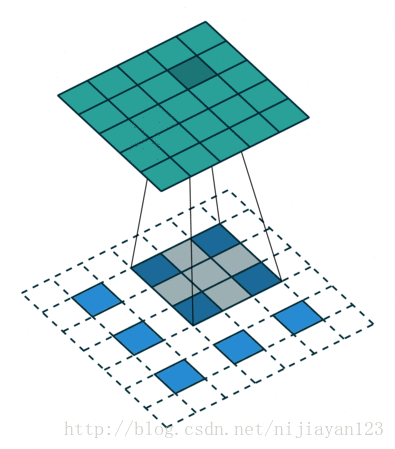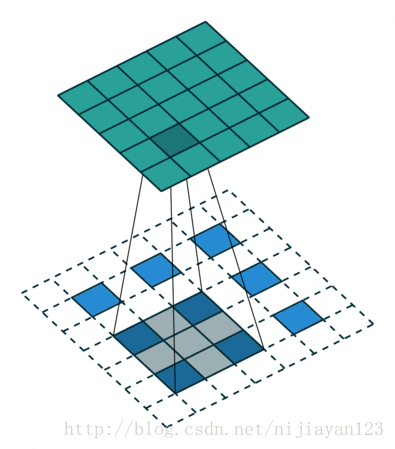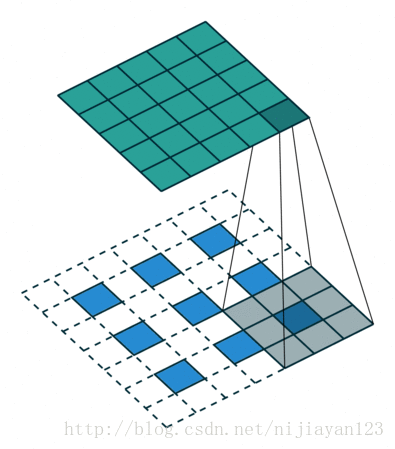
這篇論文屬於開創性的論文在影象分割領域中使用了深度學習,後面出現了各種改進性的。後面加入了隨機場和馬爾科夫鏈等一些相關操作使得整個影象分割方面效果更明顯。今年出現了Mask-RCNN 等一些優秀的論文。
參考文獻
(1)文中動畫來源
(2) Fully Convolutional Networks for Semantic Segmentation