部落格引用處（以下內容在原有部落格基礎上進行補充或更改，謝謝這些大牛的部落格指導）：
浮點數的二進位制表示(IEEE 754標準)
二進位制如何轉十進位制，十進位制如何轉二進位制

現代計算機中，一般都以IEEE 754標準儲存浮點數，這個標準的在記憶體中儲存的形式為：

對於不同長度的浮點數，階碼與小數位分配的數量不一樣，如下：

說明：短實數-float 長實數-double

由浮點數–推算出其在計算機中的二進位制表示—》二進位制：
這裡以單精度float為例子
二進位制資料的結構：

解釋說明：符號分一位，指數的移碼（階碼位）八位，尾數23位（用23位表示24位，前面隱藏一位1，對於規格化表示來說）

178.125

第一步：
先把浮點數分別把整數部分和小數部分轉換成2進位制 （即使是負數，這裡也先不考慮符號問題）
整數部分用除2取餘的方法，求得：10110010   （不用補位數，得到幾位就是幾位）
小數部分用乘2取整的方法，求得：001
合起來即是：10110010.001
轉換成二進位制的浮點數，即把小數點移動到整數位只有1，即為：1.0110010001 * 2^111，111是二進位制，由於左移了7位，所以是111
或者寫成1.0110010001 * 2^7 

第二步：
把浮點數轉換二進位制後，這裡基本已經可以得出對應3部分的值了
數符：由於浮點數是整數，故為0.(負數為1)

階碼 : 階碼是需要作移碼運算，在轉換出來的二進位制數裡，階數是111(十進位制為7)，對於單精度的浮點數，偏移值為01111111(127)[偏移量的計算是：2^(e-1)-1, e為階碼的位數，即為8，因此偏移值是127]，即：111+01111111 = 10000110 或者直接算 127+7=134 的二進位制

尾數：小數點後面的數，即0110010001   這裡1被預設隱藏

 

最終根據位置填到對位的位置上：

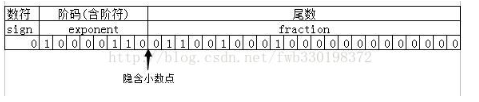
小數點前面的1去哪裡了？
由於尾數部分是規格化表示的，最高位總是“1”，所以這是直接隱藏掉，同時也節省了1個位出來儲存小數，提高精度

由二進位制數–推算出其浮點數—》浮點數：
符號位
在最高二進位制位上分配一位表示浮點數的符號，0表示正數，1表示負數

階碼位
在符號位的右邊分配8位用來儲存指數，IEEE754標準規定階碼儲存的是指數對應的移碼，而不是指數的原碼或者補碼

移碼的幾何意義：把真值（實際值，十進位制數）對映到一個正數域，其特點是可以直觀的反應兩個真值的大小，即移碼大的真值也大，基於這個特點，對計算機來說用移碼比較兩個真值的大小非常簡單，只要高位對齊後逐個比較即可，不需要考慮符號的問題。

由於階碼實際儲存的是指數的移碼，所以指數與階碼之間的換算關係就是指數與它的移碼之間的換算關係，假設指數的真值為e，階碼為E，則有E = e+(2^n-1 -1),其中 2 ^ n-1 -1 是IEEE754標準中規定的偏移量，n=8是階碼的二進位制位數（固定就是8）

尾數
最右邊連續分配的23位有效數字，IEEE754規定以原碼錶示，科學計數法進行規格化的目的是保證浮點數的唯一性，如同十進位制規格化的要求1 <= |a| < 10 ，二進位制數值規格化後的尾數形式為1.xyz ，滿足1 <= |a| < 2 ,而為了節約儲存空間，講複合規格化尾數的首個1省略了，這樣表面上是23位，卻表示了24位二進位制數。

計算：
-16 二進位制表示 1100-0001-1000-0000-0000-0000-0000-0000
先算階碼8位，算出來二進位制數轉10進位制的值A，比如100-0001-1 對應131（十進位制）
然後算出指數（底為2） Z = A-127 (包括正負)
再然後計算尾數值W，如000-0000-0000-0000-0000-0000 得到1.00000000000000000000000
最後計算數值 R = W * 2 ^ Z (-16)

Ps

• 1-0.9的浮點數計算並不等於0.1 所以以後類似浮點數值相等比較的，還是用大於小於的方式來比較是否相等。