Minkowski-P範數

兩個n維變數a(x11,x12,…,x1n)與b(x21,x22,…,x2n)間的閔可夫斯基距離(其中p是一個變引數)定義為：

• 當p=1時，就是曼哈頓距離
• 當p=2時，就是歐氏距離
• 當p→∞時，就是切比雪夫距離

根據變引數的不同，閔氏距離可以表示一類的距離。​此距離又叫做P範數

p-範數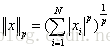：，即向量元素絕對值的p次方和的1/p次冪，matlab呼叫函式norm(x, p)。

Frobenius-弗羅貝尼烏斯範數

弗羅貝尼烏斯範數（Frobenius norm）是P範數在P=2時的一種特例，在希爾伯特空間中又叫做（ Hilbert–Schmidt norm），這個範數可用不同的方式定義：

這裡 A^* 表示 A 的共軛轉置，σ_i 是 A 的奇異值，並使用了跡函式。弗羅貝尼烏斯範數與 Kⁿ 上歐幾里得範數非常類似，來自所有矩陣的空間上一個內積。

弗羅貝尼烏斯範範數是服從乘法的且在數值線性代數中非常有用。這個範數通常比誘導範數容易計算。