2. 程式人生 > >Huffman編碼的C語言實現

Huffman編碼的C語言實現

阿新 • • 發佈：2019-01-09

實驗原理

Huffman 編碼

（1） Huffman Coding (霍夫曼編碼)是一種無失真編碼的編碼方式，Huffman 編碼是可變字長編碼(VLC)的一種。
（2）Huffman 編碼基於信源的概率統計模型，它的基本思路是，出現概率大的信源符號編長碼，出現概率小的信源符號編短碼，從而使平均碼長最小。
（3）在程式實現中常使用一種叫做樹的資料結構實現 Huffman 編碼，由它編出的碼是即時碼。

Huffman編碼的資料結構

typedef struct huffman_node_tag
{
    unsigned char isLeaf;//是否為樹葉
    unsigned
 
 long count;//節點代表的符號加權和
    struct huffman_node_tag *parent;//父節點指標

    union//共同體：如果是葉節點，則只能有symbol，如果是非葉節點，只能有左右孩子指標
    {
        struct
        {
            struct huffman_node_tag *zero, *one;//左右孩子指標
        };
        unsigned char symbol;//符號，葉節點帶有的字元
    };
} huffman_node;
typedef struct huffman_code_tag
{
    /*以位元為單位的程式碼的長度。 */
 

    unsigned long numbits;
    /* The bits that make up this code. The first
       bit is at position 0 in bits[0]. The second
       bit is at position 1 in bits[0]. The eighth
       bit is at position 7 in bits[0]. The ninth
       bit is at position 0 in bits[1]. */
    unsigned char *bits;//指向該碼位元串的指標

} huffman_code;

Huffman 編碼的方法

（1）統計符號的發生概率
（2）把頻率按從小到大的順序排列
（3）每一次選出最小的兩個值，作為二叉樹的兩個葉子節點，將和作為它們的根節點， 這兩個葉子節點不再參與比較，新的根節點參與比較
（4） 重複 3，直到最後得到和為 1 的根節點
（5） 將形成的二叉樹的左節點標 0，右節點標 1，把從最上面的根節點到最下面的葉 子節點途中遇到的 0，1 序列串起來，就得到了各個符號的編碼。

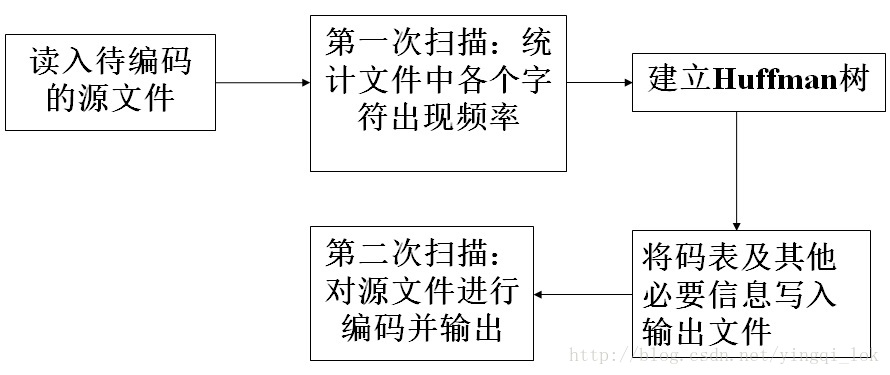
實驗流程

這裡寫圖片描述

重要程式碼分析

讀入待編碼的原始檔

int
main(int argc, char** argv)//argc命令列引數個數和argv命令列引數
{
    char memory = 0;//memory為0時，為檔案的編解碼，memory為1時為記憶體的編解碼
    char compress = 1;//compress為1時為編碼，為0時為解碼
    int opt;//getopt()的返回值 
    const char *file_in = NULL, *file_out = NULL;//輸入輸出檔名
    //step1:add by yzhang for huffman statistics
    const char *file_out_table = NULL;
    //end by yzhang
    FILE *in = stdin;
    FILE *out = stdout;
    //step1:add by yzhang for huffman statistics
    FILE * outTable = NULL;//用於txt檔案的輸出
    //end by yzhang

    /* 獲取命令列引數 */
    while((opt = getopt(argc, argv, "i:o:cdhvm")) != -1)//opt的返回值為iocdhvm或-1，getopt處理以'-’開頭的命令列引數
    {
        switch(opt)
        {
        case 'i'://輸入檔案
            file_in = optarg;//optarg為選項引數縮寫，該變數存放參數
            break;
        case 'o'://輸出檔案
            file_out = optarg;
            break;
        case 'c'://壓縮
            compress = 1;
            break;
        case 'd'://解壓縮
            compress = 0;
            break;
        case 'h'://幫助顯示使用方法
            usage(stdout);
            return 0;
        case 'v'://輸出版本版權資訊
            version(stdout);
            return 0;
        case 'm':
            memory = 1; //memory為1時為記憶體的編解碼
            break;
        // by yzhang for huffman statistics
        case 't':
            file_out_table = optarg;            
            break;
        //end by yzhang
        default:
            usage(stderr); //如果是其他情況，則將使用方法資訊送到標準錯誤檔案
            return 1;
        }
    }

getopt()函式是Linux和Unix系統環境下解析命令列的函式。在本次實驗中，命令列可設定為“-i test1.doc -o test1.huff -c -t test1.txt”

Huffman檔案編碼時的總流程

#define MAX_SYMBOLS 256
typedef huffman_node* SymbolFrequencies[MAX_SYMBOLS];//表示信源符號的陣列
typedef huffman_code* SymbolEncoder[MAX_SYMBOLS];//表示碼字的陣列，用於儲存碼錶

Huffman檔案編碼的函式

int
huffman_encode_file(FILE *in, FILE *out, FILE *out_Table)//step1:changed by yzhang for huffman statistics from (FILE *in, FILE *out) to (FILE *in, FILE *out, FILE *out_Table)表示輸出檔案結果的指標
{
    SymbolFrequencies sf;//
    SymbolEncoder *se;
    huffman_node *root = NULL;
    int rc;
    unsigned int symbol_count;
    //step2:add by yzhang for huffman statistics
    huffman_stat hs;
    //end by yzhang

/*第一次掃描，得到輸入檔案每個信源符號出現的頻率*/
    symbol_count = get_symbol_frequencies(&sf, in); //演示掃描完一遍檔案後，SF指標陣列的每個元素的構成

    //step3:add by yzhang for huffman statistics,...  get the frequency of each symbol 
    huffST_getSymFrequencies(&sf,&hs,symbol_count);
    //end by yzhang

    /*從symbolCount構建最佳表。即構建霍夫曼樹 */
    se = calculate_huffman_codes(&sf);
    root = sf[0];

    //step3:add by yzhang for huffman statistics... output the statistics to file
    huffST_getcodeword(se, &hs);
    output_huffman_statistics(&hs,out_Table);
    //end by yzhang

    /*再次掃描檔案，並使用之前構建的表將其編碼到輸出檔案中。 */
    rewind(in);
    rc = write_code_table(out, se, symbol_count);//在輸出檔案中寫入碼錶
    if(rc == 0)
        rc = do_file_encode(in, out, se);//第二次掃描，寫完碼錶後對檔案位元組按照碼錶進行編碼

    /* 釋放霍夫曼樹 */
    free_huffman_tree(root);
    free_encoder(se);
    return rc;
}

第一次掃描，統計檔案中各個字元出現頻率

1.建立一個256元素的指標陣列，用以儲存256個信源符號的頻率，其下標對應相應字元的ASCAII碼。
2.陣列中的非空元素為當前編碼檔案中實際出現的信源符號

static unsigned int
get_symbol_frequencies(SymbolFrequencies *pSF, FILE *in)//統計檔案中各個字元出現頻率
{
    int c;
    unsigned int total_count = 0;//掃描的總信源符號數，初始化為0

    /* 將所有信源符號地址初始化為NULL，使得所有字元頻率為0 */
    init_frequencies(pSF);

    /* 計算輸入檔案中每個符號的頻率。 */
    while((c = fgetc(in)) != EOF)//挨個讀取字元
    {
        unsigned char uc = c;//將讀取的字元賦給uc
        if(!(*pSF)[uc])//如果uc不存在對應的空間，即uc是一個新的符號
            (*pSF)[uc] = new_leaf_node(uc);//產生該字元的一個新的葉節點。
        ++(*pSF)[uc]->count;//如果uc不是一個新的字元，則當前字元出現的頻數累加1
        ++total_count;//總計數值加1
    }

    return total_count;//返回值為總計數值
}

new_leaf_node()函式：

static huffman_node*
new_leaf_node(unsigned char symbol)/*新建一個葉節點*/
{
    huffman_node *p = (huffman_node*)malloc(sizeof(huffman_node));
    p->isLeaf = 1;//1表示是葉節點
    p->symbol = symbol;//將新的符號的值存入symbol中
    p->count = 0;//該節點的頻數為初始化0
    p->parent = 0;//該節點父節點初始化為0
    return p;
}

建立Huffman樹並計算符號對應的Huffman碼字

1.按頻率從小到大排序並建立Huffman樹

static SymbolEncoder*
calculate_huffman_codes(SymbolFrequencies * pSF)
{
    unsigned int i = 0;
    unsigned int n = 0;
    huffman_node *m1 = NULL, *m2 = NULL;
    SymbolEncoder *pSE = NULL;

#if 0
    printf("BEFORE SORT\n");
    print_freqs(pSF);
#endif

    /* 按升序對符號頻率陣列進行排序 */
    qsort((*pSF), MAX_SYMBOLS, sizeof((*pSF)[0]), SFComp);//陣列的起始地址，陣列的元素數，每個元素的大小，比較函式的指標
    //將所有的節點按照字元概率小到大排序，可使用qsort函式對節點結構體進行排序。排序的依據是SFComp，即根據每個字元發生的概率進行排序。
#if 0   
    printf("AFTER SORT\n");
    print_freqs(pSF);
#endif

    /*得到檔案出現的字元種類數   */
    for(n = 0; n < MAX_SYMBOLS && (*pSF)[n]; ++n)
        ;

    /*
     * Construct a Huffman tree. This code is based
     * on the algorithm given in Managing Gigabytes
     * by Ian Witten et al, 2nd edition, page 34.
     * Note that this implementation uses a simple
     * count instead of probability.
     構建霍夫曼樹
     */
    for(i = 0; i < n - 1; ++i)
    {
        /* 將m1和m2設定為最小概率的兩個子集。 */
            m1 = (*pSF)[0];
        m2 = (*pSF)[1];

        /* 將m1和m2替換為一個集合{m1，m2}，其概率是m1和m2之和的概率。*/

        //合併m1、m2為非葉節點，count為二者count之和  
        //並將該非葉節點的左右孩子設為m1、m2  
        //將左右孩子的父節點指向該非葉節點  
        //將(*pSF)[0]指向該非葉節點
        (*pSF)[0] = m1->parent = m2->parent =
            new_nonleaf_node(m1->count + m2->count, m1, m2);//
        (*pSF)[1] = NULL;//1節點置空    
        /* 由於最小的兩個頻率數，進行了合併，頻率大小發生改變，所以重新排序 */
        qsort((*pSF), n, sizeof((*pSF)[0]), SFComp);
    }

    /* Build the SymbolEncoder array from the tree. */
    pSE = (SymbolEncoder*)malloc(sizeof(SymbolEncoder));
    //定義一個指標陣列，陣列中每個元素是指向碼節點的指標
    memset(pSE, 0, sizeof(SymbolEncoder));
    build_symbol_encoder((*pSF)[0], pSE);
    return pSE;
}

qsort函式是編譯器函式庫自帶的快速排序函式。函式的四個變數分別是陣列的起始地址，陣列的元素數，每個元素的大小，比較函式的指標。在本程式中，sFcomp指向自定義的用於比較的函式sFcomp（）

static int
SFComp(const void *p1, const void *p2)
{
    const huffman_node *hn1 = *(const huffman_node**)p1;
    const huffman_node *hn2 = *(const huffman_node**)p2;

    /* 用於將所有NULL排到最後 */
    if(hn1 == NULL && hn2 == NULL)
        return 0;//若兩者都為空，則返回相等
    if(hn1 == NULL)
        return 1;//若返回值為1，大於0，則hn1排到hn2後
    if(hn2 == NULL)
        return -1;////若返回值為-1，小於0，則hn2排到hn1後
    /*由小到大排列*/
    if(hn1->count > hn2->count)
        return 1;
    else if(hn1->count < hn2->count)
        return -1;

    return 0;
}

這裡寫圖片描述
2.遍歷遞迴Huffman樹，對存在的每個字元計算碼字

/*
 * build_symbol_encoder builds a SymbolEncoder by walking
 * down to the leaves of the Huffman tree and then,
 * for each leaf, determines its code.
 */
static void
build_symbol_encoder(huffman_node *subtree, SymbolEncoder *pSF)
{
    if(subtree == NULL)
        return;//判斷是否是空樹, 是則說明編碼結束，

    if(subtree->isLeaf)//判斷是否為樹葉節點，是則產生新的碼字
        (*pSF)[subtree->symbol] = new_code(subtree);
    else
    {//
        build_symbol_encoder(subtree->zero, pSF);//遍歷左子樹，呼叫build_symbol_encoder函式自身
        build_symbol_encoder(subtree->one, pSF);//遍歷右子數
    }
}

new_code從霍夫曼樹葉中構建一個huffman_code

static huffman_code*
new_code(const huffman_node* leaf)
{
    /* 通過走到根節點然後反轉位來構建huffman程式碼，
    因為霍夫曼程式碼是通過走下樹來計算的。*/
    //採用向上回溯的方法
    unsigned long numbits = 0;//表示碼長，以位為單位
    unsigned char* bits = NULL;//表示指向碼字的指標
    huffman_code *p;

    while(leaf && leaf->parent)//用來判斷節點和父節點是否存在，leaf為NULL時，不進行編碼；parent為NULL時，已經到達樹根不在編碼
    {
        huffman_node *parent = leaf->parent;
        unsigned char cur_bit = (unsigned char)(numbits % 8);//current_bit為當前在bits[]的第幾位

        unsigned long cur_byte = numbits / 8;//current_byte

        /* 如果碼字長度超過一個位元組，那麼就在分配一個位元組 */
        if(cur_bit == 0)
        {
            size_t newSize = cur_byte + 1;
            bits = (char*)realloc(bits, newSize);
            /*realloc()函式先判斷當前的指標是否有足夠的連續空間，如果有，擴大bits指向的地址，並且將bits返回，如果空間不夠，先按照newsize指定的大小分配空間，將原有資料從頭到尾拷貝到新分配的記憶體區域，而後釋放原來bits所指記憶體區域(注意:原來指標是自動釋放，不需要使用free)，同時返回新分配的記憶體區域的首地址。即重新分配儲存器塊的地址。*/
            bits[newSize - 1] = 0; /* Initialize the new byte. */
        }

//如果是左孩子，則不用改變數值，因為初始化為0。如果是右孩子，則將該位置1
        if(leaf == parent->one)
            bits[cur_byte] |= 1 << cur_bit;//將1左移至cur_bit，再將其與bits[cur_byte]進行或的操作

        ++numbits;//碼字位數加1
        leaf = parent;//下一位的碼字在當前碼字的父節點一級
    }

    if(bits)//將現有的碼字進行反轉
        reverse_bits(bits, numbits);

    p = (huffman_code*)malloc(sizeof(huffman_code));
    p->numbits = numbits;//碼長賦給節點的numbits
    p->bits = bits;//碼字付給節點的bits
    return p;//返回值為碼字
}

對碼字進行倒序的函式reverse（）

static void
reverse_bits(unsigned char* bits, unsigned long numbits)
{
    unsigned long numbytes = numbytes_from_numbits(numbits);//將numbits除8後上取整得到numbytes
    unsigned char *tmp =
        (unsigned char*)alloca(numbytes);//alloca()是記憶體分配函式，在棧上申請空間，用完後馬上就釋放
    unsigned long curbit;
    long curbyte = 0;//記錄即將要反轉的二進位制碼所在的的陣列下標

    memset(tmp, 0, numbytes); //將陣列tmp[numbytes]所有元素置為為0

    for(curbit = 0; curbit < numbits; ++curbit)
    {
        unsigned int bitpos = curbit % 8;//表示curbit不是8的倍數時需要左移的位數

        if(curbit > 0 && curbit % 8 == 0)//curbit為8的倍數時，進入下一個位元組
            ++curbyte;

        tmp[curbyte] |= (get_bit(bits, numbits - curbit - 1) << bitpos);
    }

    memcpy(bits, tmp, numbytes);//將tmp臨時陣列內容拷貝到bits陣列中
}

get_bits函式

//第i位在第 i/8 位元組的第 i%8 位，把這一位移到位元組最低位，和 0000 0001 做與，從而只留下這一位，
static unsigned char
get_bit(unsigned char* bits, unsigned long i)
{
    return (bits[i / 8] >> i % 8) & 1;
}

3.將碼錶寫入檔案

static int
write_code_table(FILE* out, SymbolEncoder *se, unsigned int symbol_count)
{
    unsigned long i, count = 0;

    /* 計算se中的字元種類數. */
    for(i = 0; i < MAX_SYMBOLS; ++i)
    {
        if((*se)[i])
            ++count;
    }

    /* Write the number of entries in network byte order. */
    i = htonl(count);    //在網路傳輸中，採用big-endian序，對於0x0A0B0C0D ，傳輸順序就是0A 0B 0C 0D ，
    //因此big-endian作為network byte order，little-endian作為host byte order。
    //little-endian的優勢在於unsigned char/short/int/long型別轉換時，儲存位置無需改變
    if(fwrite(&i, sizeof(i), 1, out) != 1)
        return 1;//將字元種類的個數寫入檔案

    /* Write the number of bytes that will be encoded. */
    symbol_count = htonl(symbol_count);
    if(fwrite(&symbol_count, sizeof(symbol_count), 1, out) != 1)
        return 1;//將字元數寫入檔案

    /* Write the entries. */
    for(i = 0; i < MAX_SYMBOLS; ++i)
    {
        huffman_code *p = (*se)[i];
        if(p)
        {
            unsigned int numbytes;
            /* 寫入1位元組的符號 */
            fputc((unsigned char)i, out);
            /* 寫入一位元組的碼長 */
            fputc(p->numbits, out);
            /* 寫入numbytes位元組的碼字*/
            numbytes = numbytes_from_numbits(p->numbits);
            if(fwrite(p->bits, 1, numbytes, out) != numbytes)
                return 1;
        }
    }

    return 0;
}

第二次掃描檔案，對檔案查表進行Huffman編碼

static int
do_file_encode(FILE* in, FILE* out, SymbolEncoder *se)
{
    unsigned char curbyte = 0;
    unsigned char curbit = 0;
    int c;

    while((c = fgetc(in)) != EOF)//遍歷檔案的每一個字元
    {
        unsigned char uc = (unsigned char)c;
        huffman_code *code = (*se)[uc];//查表
        unsigned long i;
        /*將碼字寫入檔案*/
        for(i = 0; i < code->numbits; ++i)
        {
            /* Add the current bit to curbyte. */
            curbyte |= get_bit(code->bits, i) << curbit;

            /* If this byte is filled up then write it
             * out and reset the curbit and curbyte. */
            if(++curbit == 8)
            {
                fputc(curbyte, out);
                curbyte = 0;
                curbit = 0;
            }
        }
    }

輸出統計結果

定義用於輸出統計結果的結構體

typedef struct huffman_statistics_result
{
    float freq[256];//用於記錄每個信源符號出現的頻次
    unsigned long numbits[256];
    unsigned char bits[256][100];//用來存放碼字，規定每個碼字的最大長度為100
}huffman_stat;

int huffST_getSymFrequencies(SymbolFrequencies *SF, huffman_stat *st,int total_count)
{
    int i,count =0;
    for(i = 0; i < MAX_SYMBOLS; ++i)
    {   
        if((*SF)[i])
        {
            st->freq[i]=(float)(*SF)[i]->count/total_count;
            count+=(*SF)[i]->count;
        }
        else 
        {
            st->freq[i]= 0;
        }
    }
    if(count==total_count)
        return 1;
    else
        return 0;
}

int huffST_getcodeword(SymbolEncoder *se, huffman_stat *st)
{
    unsigned long i,j;

    for(i = 0; i < MAX_SYMBOLS; ++i)
    {
        huffman_code *p = (*se)[i];
        if(p)
        {
            unsigned int numbytes;
            st->numbits[i] = p->numbits;
            numbytes = numbytes_from_numbits(p->numbits);
            for (j=0;j<numbytes;j++)
                st->bits[i][j] = p->bits[j];
        }
        else
            st->numbits[i] =0;
    }

    return 0;
}

void output_huffman_statistics(huffman_stat *st,FILE *out_Table)
{
    int i,j;
    unsigned char c;
    fprintf(out_Table,"symbol\t   freq\t   codelength\t   code\n");
    for(i = 0; i < MAX_SYMBOLS; ++i)
    {   
        fprintf(out_Table,"%d\t   ",i);
        fprintf(out_Table,"%f\t   ",st->freq[i]);
        fprintf(out_Table,"%d\t    ",st->numbits[i]);
        if(st->numbits[i])
        {
            for(j = 0; j < st->numbits[i]; ++j)
            {
                c =get_bit(st->bits[i], j);
                fprintf(out_Table,"%d",c);
            }
        }
        fprintf(out_Table,"\n");
    }
}

實驗結果分析

實驗結果

檔案型別 平均碼長 信源熵 原檔案大小(kb) 壓縮後文件大小(kb) 壓縮比
doc 2.743322 2.56875342 26 10 2.6
jpg 7.997263 7.977105663 2137 2137 1
avi 7.985401 7.977105663 3136 3132 1.0012
excel 7.320745 7.282297404 87 81 1.07
pdf 7.93953 7.917915356 207 206 1
mp4 8.00 7.917915356 12134 12135 1
rar 8.00004 7.998742279 13225 13226 0.9999
mpg 7.817351 7.791074385 3984 3983 1
ppt 7.947827 7.934968073 5014 4983 1.0062

各樣本檔案的概率分佈圖

檔案型別 概率分佈圖
doc 這裡寫圖片描述
jpg 這裡寫圖片描述
avi 這裡寫圖片描述
excel 這裡寫圖片描述
pdf 這裡寫圖片描述
mp4 這裡寫圖片描述
rar 這裡寫圖片描述
mpg 這裡寫圖片描述
ppt 這裡寫圖片描述

實驗結果分析

由各個檔案型別經壓縮編碼後的平均碼長和信源熵可以看出，各檔案型別的平均碼長和信源熵大小基本相同，平均碼長無限逼近信源熵，可以驗證無失真編碼的平均碼長界限定理。
由編碼效率可以看出，doc檔案、excel檔案、ppt檔案和avi檔案的編碼效率較高，通過檔案概率分佈圖可以看出，由於霍夫曼編碼是可變長編碼，因此當各個信源符號概率分佈差異較大，且概率較大的信源符號個數很少時，霍夫曼編碼的壓縮效果最好。

存在的疑問

為什麼碼長為8，但編出的碼字並不是8位的？
這裡寫圖片描述

相關推薦

哈夫曼編碼C語言實現

#include "stdafx.h" #include <stdio.h> #include <stdlib.h> #define debug 0 typedef struct HuffNode {int parent;int lchild;in

Huffman編碼的C語言實現

實驗原理 Huffman 編碼 （1） Huffman Coding (霍夫曼編碼)是一種無失真編碼的編碼方式，Huffman 編碼是可變字長編碼(VLC)的一種。 （2）Huffman 編碼基於信源的概率統計模型，它的基本思路是，出現概率大的信源符號

二十四進制編碼串轉換為32位無符號整數（C語言實現）

bool while open 參數錯誤 hint div 第一個字符 bsp opened typedef int BOOL; #define TRUE 1; #define FALSE 0; #define UINT_MAX 0xffffffff

Huffuman編碼與譯碼C語言實現

一、Huffman編碼  Huffuman編碼的過程主要分為兩步，第一步根據字元出現的權值構建Huffuman樹，第二步，遍歷Huffuman樹找出對應字元的編碼 1. 構建Huffuman樹程式碼如下： typedef struct iNode {  

不依賴任何系統API，用c語言實現gbk/utf8/unicode編碼轉換

轉載地址:https://blog.csdn.net/bladeandmaster88/article/details/54837338 漢字'我' Unicode編碼是0x6211       01100010 00010001 UTF8編碼是&

[原始碼和文件分享]C語言實現huffman編解碼與壓縮文字

1 原理 哈夫曼編碼(Huffman Coding)，又稱霍夫曼編碼，是一種編碼方式，哈夫曼編碼是可變字長編碼(VLC)的一種。Huffman於1952年提出一種編碼方法，該方法完全依據字元出現概率來構造異字頭的平均長度最短的碼字，有時稱之為最佳編碼，一般就叫做Huffman編碼(有時也稱為霍夫

資料結構——哈夫曼樹的實現以及編碼（C語言實現）

1、問題描述       利用哈夫曼編碼進行通訊可以大大提高通道利用率，縮簡訊息傳輸時間，降低傳輸成本。構造哈夫曼樹時，首先將由n個字 符形成的n個葉子結點存放到陣列HuffNode的前n個分量中，然後根據哈夫曼方法的基本思想，不斷將兩個較小的子樹合併為一個

c語言實現赫夫曼樹的構建以及生成赫夫曼編碼（《資料結構》演算法6.12）

這個程式是根據《資料結構》演算法6.12用c語言實現的程式，赫夫曼樹就不多說了，直接看程式碼，程式碼上都有註釋。 下面程式碼： #include<stdio.h> #include<iostream> #include<stdlib.h>

資料結構之---C語言實現哈夫曼樹和編碼

//哈夫曼樹 //楊鑫 #include <stdio.h> #include <stdlib.h> typedef int ElemType; struct BTreeNode { ElemType data; struct BTr

C語言實現windows1251編碼轉utf-8編碼

windows1251是俄羅斯本地的一種編碼，不通用。mini xml好像無法解析，但客戶就是提供一個這種編碼檔案的url，讓你解析裡面的資料。 開源的編碼轉換庫又太大，只好用C語言寫一個。有些字元轉換沒什麼規律，只能一一對應，很耿直的轉換方式，哈哈~~，不過以後如果遇到相

基於Huffman樹的檔案壓縮原理及C語言實現（二）

在上文基於Huffman樹的檔案壓縮原理及C語言實現（一）中已經介紹並實現瞭如何建立Huffman樹，得到Huffman編碼，這篇我們將會接著說。如何通過Huffman樹，實現檔案壓縮。 實現思路 任何檔案都可以看作是由位元組組成的位元組塊，將位元組看作

貪心演算法之哈夫曼編碼（C語言實現）

如題 問題描述:現有一個文字檔案，其中包含的字元資料出現的次數各不相同，先要求對該文字中包含的字元進行編碼，使文字佔用的位數更小。 問題分析 我們知道檔案的儲存都是以二進位制數表示的，如：字元c可以表示為010101…之類的。因 為不同的作業

Base64編碼解碼C語言實現

static const char *codes = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"; static const unsigned char map[256] = {

c語言實現哈夫曼編碼

#include <stdio.h>#include <math.h>#define MAX 100#define MAXSYMBS 30#define MAXNODE 59#define DEEP 10 typedef struct{ float w

DCT變換編碼及C語言實現

離散餘弦變換（Discrete Cosine Transform，簡稱DCT變換）是一種與傅立葉變換緊密相關的數學運算。在傅立葉級數展開式中，如果被展開的函式是實偶函式，那麼其傅立葉級數中只包含餘弦項，再將其離散化可匯出餘弦變換，因此稱之為離散餘弦變換。  

遺傳算法的C語言實現(二)

print 比較 詳細 author 當前 cross max r+ 訪問 上一次我們使用遺傳算法求解了一個較為復雜的多元非線性函數的極值問題，也基本了解了遺傳算法的實現基本步驟。這一次，我再以經典的TSP問題為例，更加深入地說明遺傳算法中選擇、交叉、變異等核心步

C語言實現粒子群算法（PSO）二

計算 default img 第一個元素 1.4 best 實驗 atl 說過 上一回說了基本粒子群算法的實現，並且給出了C語言代碼。這一篇主要講解影響粒子群算法的一個重要參數---w。我們已經說過粒子群算法的核心的兩個公式為： Vid(k+1)=w*Vid(k)+c1*r

遺傳算法的C語言實現(一):以非線性函數求極值為例

選中 algorithm 利用 mail 進化 lock gcc 最大值 -s 以前搞數學建模的時候，研究過(其實也不算是研究，只是大概了解)一些人工智能算法，比如前面已經說過的粒子群算法(PSO),還有著名的遺傳算法(GA),模擬退火算法(SA),蟻群算法(A

C語言實現粒子群算法(PSO)一

mat 遺傳 基於 [1] 沒有 實驗 規模 直觀 解決 最近在溫習C語言，看的書是《C primer Plus》，忽然想起來以前在參加數學建模的時候，用過的一些智能算法，比如遺傳算法、粒子群算法、蟻群算法等等。當時是使用MATLAB來實現的，而且有些MATLAB自帶了工具

(續)順序表之單循環鏈表(C語言實現)

include 作者 指針 順序 gb2 mark oos case 循環 單循環鏈表和單鏈表的唯一差別在於單循環鏈表的最後一個節點的指針域指向第一個節點, 使得整個鏈表形成一個環. C實現代碼例如以下: #include<stdio.h>