經典演算法研究系列:六、教你初步瞭解KMP演算法、updated
教你初步瞭解KMP演算法
作者: July 、saturnma、上善若水。 時間; 二零一一年一月一日
-----------------------
本文參考:資料結構(c語言版) 李雲清等編著、演算法導論
引言:
在文字編輯中,我們經常要在一段文字中某個特定的位置找出 某個特定的字元或模式。
由此,便產生了字串的匹配問題。
本文由簡單的字串匹配演算法開始,再到KMP演算法,由淺入深,教你從頭到尾徹底理解KMP演算法。
來看演算法導論一書上關於此字串問題的定義:
假設文字是一個長度為n的陣列T[1...n],模式是一個長度為m<=n的陣列P[1....m]。
進一步假設P和T的元素都是屬於有限字母表Σ.中的字元。
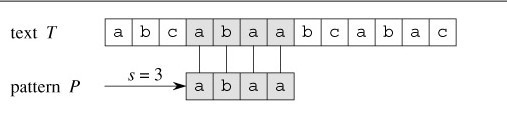
依據上圖,再來解釋下字串匹配問題。目標是找出所有在文字T=abcabaabcaabac中的模式P=abaa所有出現。
該模式僅在文字中出現了一次,在位移s=3處。位移s=3是有效位移。
第一節、簡單的字串匹配演算法
簡單的字串匹配演算法用一個迴圈來找出所有有效位移,
該迴圈對n-m+1個可能的每一個s值檢查條件P[1....m]=T[s+1....s+m]。
NAIVE-STRING-MATCHER(T, P)
1 n ← length[T]
2 m ← length[P]
3 for s ← 0 to n - m
4 do if P[1 ‥ m] = T[s + 1 ‥ s + m]
//對n-m+1個可能的位移s中的每一個值,比較相應的字元的迴圈必須執行m次。
5 then print "Pattern occurs with shift" s

簡單字串匹配演算法,上圖針對文字T=acaabc 和模式P=aab。
上述第4行程式碼,n-m+1個可能的位移s中的每一個值,比較相應的字元的迴圈必須執行m次。
所以,在最壞情況下,此簡單模式匹配演算法的執行時間為O((n-m+1)m)。
--------------------------------
下面我再來舉個具體例子,並給出一具體執行程式:
對於目的字串target是banananobano,要匹配的字串pattern是nano,的情況,
下面是匹配過程,原理很簡單,只要先和target字串的第一個字元比較,
如果相同就比較下一個,如果不同就把pattern右移一下,
之後再從pattern的每一個字元比較,這個演算法的執行過程如下圖。
//index表示的每n次匹配的情形。

#include<iostream>
#include<string>
using namespace std;
int match(const string& target,const string& pattern)
{
int target_length = target.size();
int pattern_length = pattern.size();
int target_index = 0;
int pattern_index = 0;
while(target_index < target_length && pattern_index < pattern_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else
{
target_index -= (pattern_index-1);
pattern_index = 0;
}
}
if(pattern_index == pattern_length)
{
return target_index - pattern_length;
}
else
{
return -1;
}
}
int main()
{
cout<<match("banananobano","nano")<<endl;
return 0;
}
//執行結果為4。
上面的演算法進間複雜度是O(pattern_length*target_length),
我們主要把時間浪費在什麼地方呢,
觀查index =2那一步,我們已經匹配了3個字元,而第4個字元是不匹配的,這時我們已經匹配的字元序列是nan,
此時如果向右移動一位,那麼nan最先匹配的字元序列將是an,這肯定是不能匹配的,
之後再右移一位,匹配的是nan最先匹配的序列是n,這是可以匹配的。
如果我們事先知道pattern本身的這些資訊就不用每次匹配失敗後都把target_index回退回去,
這種回退就浪費了很多不必要的時間,如果能事先計算出pattern本身的這些性質,
那麼就可以在失配時直接把pattern移動到下一個可能的位置,
把其中根本不可能匹配的過程省略掉,
如上表所示我們在index=2時失配,此時就可以直接把pattern移動到index=4的狀態,
kmp演算法就是從此出發。
第二節、KMP演算法
2.1、 覆蓋函式(overlay_function)
覆蓋函式所表徵的是pattern本身的性質,可以讓為其表徵的是pattern從左開始的所有連續子串的自我覆蓋程度。
比如如下的字串,abaabcaba
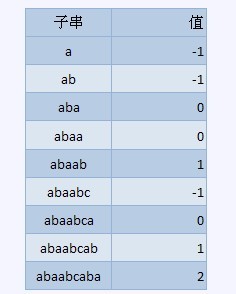
由於計數是從0始的,因此覆蓋函式的值為0說明有1個匹配,對於從0還是從來開始計數是偏好問題,
具體請自行調整,其中-1表示沒有覆蓋,那麼何為覆蓋呢,下面比較數學的來看一下定義,比如對於序列
a0a1...aj-1 aj
要找到一個k,使它滿足
a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
而沒有更大的k滿足這個條件,就是說要找到儘可能大k,使pattern前k字元與後k字元相匹配,k要儘可能的大,
原因是如果有比較大的k存在,而我們選擇較小的滿足條件的k,
那麼當失配時,我們就會使pattern向右移動的位置變大,而較少的移動位置是存在匹配的,這樣我們就會把可能匹配的結果丟失。
比如下面的序列,
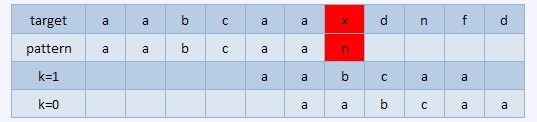
在紅色部分失配,正確的結果是k=1的情況,把pattern右移4位,如果選擇k=0,右移5位則會產生錯誤。
計算這個overlay函式的方法可以採用遞推,可以想象如果對於pattern的前j個字元,如果覆蓋函式值為k
a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
則對於pattern的前j+1序列字元,則有如下可能
⑴ pattern[k+1]==pattern[j+1] 此時overlay(j+1)=k+1=overlay(j)+1
⑵ pattern[k+1]≠pattern[j+1] 此時只能在pattern前k+1個子符組所的子串中找到相應的overlay函式,h=overlay(k),如果此時pattern[h+1]==pattern[j+1],則overlay(j+1)=h+1否則重複(2)過程.
下面給出一段計算覆蓋函式的程式碼:
#include<iostream>
#include<string>
using namespace std;
void compute_overlay(const string& pattern)
{
const int pattern_length = pattern.size();
int *overlay_function = new int[pattern_length];
int index;
overlay_function[0] = -1;
for(int i=1;i<pattern_length;++i)
{
index = overlay_function[i-1];
//store previous fail position k to index;
while(index>=0 && pattern[i]!=pattern[index+1])
{
index = overlay_function[index];
}
if(pattern[i]==pattern[index+1])
{
overlay_function[i] = index + 1;
}
else
{
overlay_function[i] = -1;
}
}
for(i=0;i<pattern_length;++i)
{
cout<<overlay_function[i]<<endl;
}
delete[] overlay_function;
}
int main()
{
string pattern = "abaabcaba";
compute_overlay(pattern);
return 0;
}
執行結果為:
-1
-1
0
0
1
-1
0
1
2
Press any key to continue
-------------------------------------
2.2、kmp演算法
有了覆蓋函式,那麼實現kmp演算法就是很簡單的了,我們的原則還是從左向右匹配,但是當失配發生時,我們不用把target_index向回移動,target_index前面已經匹配過的部分在pattern自身就能體現出來,只要動pattern_index就可以了。
當發生在j長度失配時,只要把pattern向右移動j-overlay(j)長度就可以了。
如果失配時pattern_index==0,相當於pattern第一個字元就不匹配,
這時就應該把target_index加1,向右移動1位就可以了。
ok,下圖就是KMP演算法的過程(紅色即是採用KMP演算法的執行過程):
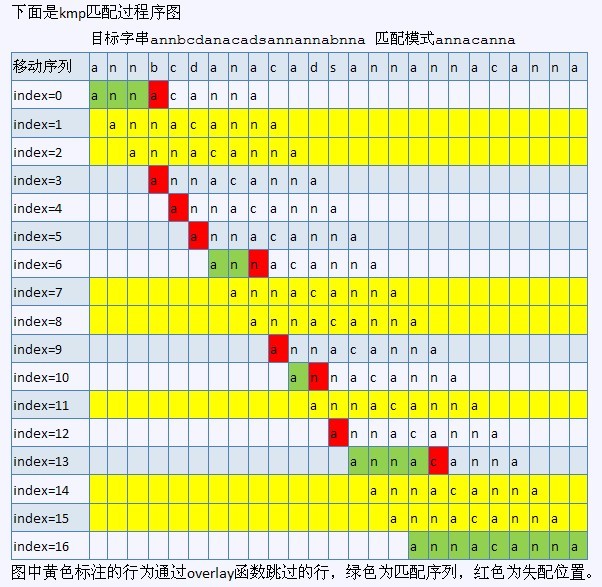
另一作者saturnman發現,在上述KMP匹配過程圖中,index=8和index=11處畫錯了。還有,anaven也早已發現,index=3處也畫錯了。非常感謝。但圖已無法修改,見諒。
KMP 演算法可在O(n+m)時間內完成全部的串的模式匹配工作。
ok,最後給出KMP演算法實現的c++程式碼:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
int kmp_find(const string& target,const string& pattern)
{
const int target_length = target.size();
const int pattern_length = pattern.size();
int * overlay_value = new int[pattern_length];
overlay_value[0] = -1;
int index = 0;
for(int i=1;i<pattern_length;++i)
{
index = overlay_value[i-1];
while(index>=0 && pattern[index+1]!=pattern[i])
{
index = overlay_value[index];
}
if(pattern[index+1]==pattern[i])
{
overlay_value[i] = index +1;
}
else
{
overlay_value[i] = -1;
}
}
//match algorithm start
int pattern_index = 0;
int target_index = 0;
while(pattern_index<pattern_length&&target_index<target_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else if(pattern_index==0)
{
++target_index;
}
else
{
pattern_index = overlay_value[pattern_index-1]+1;
}
}
if(pattern_index==pattern_length)
{
return target_index-pattern_index;
}
else
{
return -1;
}
delete [] overlay_value;
}
int main()
{
string source = " annbcdanacadsannannabnna";
string pattern = " annacanna";
cout<<kmp_find(source,pattern)<<endl;
return 0;
}
//執行結果為 -1.
第三節、kmp演算法的來源
kmp如此精巧,那麼它是怎麼來的呢,為什麼要三個人合力才能想出來。其實就算沒有kmp演算法,人們在字元匹配中也能找到相同高效的演算法。這種演算法,最終相當於kmp演算法,只是這種演算法的出發點不是覆蓋函式,不是直接從匹配的內在原理出發,而使用此方法的計算的覆蓋函式過程式複雜且不易被理解,但是一但找到這個覆蓋函式,那以後使用同一pattern匹配時的效率就和kmp一樣了,其實這種演算法找到的函式不應叫做覆蓋函式,因為在尋找過程中根本沒有考慮是否覆蓋的問題。
說了這麼半天那麼這種方法是什麼呢,這種方法是就大名鼎鼎的確定的有限自動機(Deterministic finite state automaton DFA),DFA可識別的文法是3型文法,又叫正規文法或是正則文法,既然可以識別正則文法,那麼識別確定的字串肯定不是問題(確定字串是正則式的一個子集)。對於如何構造DFA,是有一個完整的演算法,這裡不做介紹了。在識別確定的字串時使用DFA實在是大材小用,DFA可以識別更加通用的正則表示式,而用通用的構建DFA的方法來識別確定的字串,那這個overhead就顯得太大了。
kmp演算法的可貴之處是從字元匹配的問題本身特點出發,巧妙使用覆蓋函式這一表徵pattern自身特點的這一概念來快速直接生成識別字串的DFA,因此對於kmp這種演算法,理解這種演算法高中數學就可以了,但是如果想從無到有設計出這種演算法是要求有比較深的數學功底的。
第四節、精確字元匹配的常見演算法的解析
KMP演算法:
KMP就是串匹配演算法
運用自動機原理
比如說
我們在S中找P
設P={ababbaaba}
我們將P對自己匹配
下面是求的過程:{依次記下匹配失敗的那一位}
[2]ababbaaba
.......ababbaaba[1]
[3]ababbaaba
.........ababbaaba[1]
[4]ababbaaba
.........ababbaaba[2]
[5]ababbaaba
.........ababbaaba[3]
[6]ababbaaba
................ababbaaba[1]
[7]ababbaaba
................ababbaaba[2]
[8]ababbaaba
..................ababbaaba[2]
[9]ababbaaba
..................ababbaaba[3]
得到Next陣列『0,1,1,2,3,1,2,2,3』
主過程:
[1]i:=1 j:=1
[2]若(j>m)或(i>n)轉[4]否則轉[3]
[3]若j=0或a[i]=b[j]則【inc(i)inc(j)轉[2]】否則【j:=next[j]轉2】
[4]若j>m則return(i-m)否則return -1;
若返回-1表示失敗,否則表示在i-m處成功
BM演算法也是一種快速串匹配演算法,KMP演算法的主要區別是匹配操作的方向不同。雖然T右移的計算方法卻發生了較大的變化。
為方便討論,T="dist:c->{dist稱為滑動距離函式,它給出了正文中可能出現的任意字元在模式中的位置。函式 m – jj為 dist(m+1 若c = tm
例如,pattern",則p)a)t)dist(= 2,r)n)BM演算法的基本思想是:假設將主串中自位置i + dist(si)位置開始重新進行新一輪的匹配,其效果相當於把模式和主串向右滑過一段距離si),即跳過si)個字元而無需進行比較。
下面是一個S ="T="BM演算法可以大大加快串匹配的速度。
下面是KMP演算法部分,把呼叫BM函式便可。
Horspool演算法這個演算法是由R.Nigel Horspool在1980年提出的。其滑動思想非常簡單,就是從後往前匹配模式串,若在某一位失去匹配,此位對應的文字串字元為c,那就將模式串向右滑動,使模式串之前最近的c對準這一位,再從新從後往前檢查。那如果之前找不到c怎麼辦?那好極了,直接將整個模式串滑過這一位。例如:
文字串:abdabaca
模式串:baca倒數第2位失去匹配,模式串之前又沒有d,那模式串就可以整個滑過,變成這樣:
文字串:abdabaca
模式串: baca發現倒數第1位就失去匹配,之前1位有c,那就向右滑動1位:
文字串:abdabaca
模式串: baca實現程式碼:
SUNDAY演算法:
BM演算法的改進的演算法SUNDAY--Boyer-Moore-Horspool-Sunday Aglorithm
BM演算法優於KMP
SUNDAY 演算法描述:字串查詢演算法中,最著名的兩個是KMP演算法(Knuth-Morris-Pratt)和BM演算法(Boyer-Moore)。兩個演算法在最壞情況下均具有線性的查詢時間。但是在實用上,KMP演算法並不比最簡單的c庫函式strstr()快多少,而BM演算法則往往比KMP演算法快上3-5倍。但是BM演算法還不是最快的演算法,這裡介紹一種比BM演算法更快一些的查詢演算法即Sunday演算法。例如我們要在"substring searching algorithm"查詢"search",剛開始時,把子串與文字左邊對齊:
substring searching algorithm
search
^
結果在第二個字元處發現不匹配,於是要把子串往後移動。但是該移動多少呢?這就是各種演算法各顯神通的地方了,最簡單的做法是移動一個字元位置;KMP是利用已經匹配部分的資訊來移動;BM演算法是做反向比較,並根據已經匹配的部分來確定移動量。這裡要介紹的方法是看緊跟在當前子串之後的那個字元(上圖中的 'i')。顯然,不管移動多少,這個字元是肯定要參加下一步的比較的,也就是說,如果下一步匹配到了,這個字元必須在子串內。所以,可以移動子串,使子串中的最右邊的這個字元與它對齊。現在子串'search'中並不存在'i',則說明可以直接跳過一大片,從'i'之後的那個字元開始作下一步的比較,如下圖:
substring searching algorithm
search^比較的結果,第一個字元就不匹配,再看子串後面的那個字元,是'r',它在子串中出現在倒數第三位,於是把子串向前移動三位,使兩個'r'對齊,如下:
substring searching algorithm
search^哈!這次匹配成功了!回顧整個過程,我們只移動了兩次子串就找到了匹配位置,可以證明,用這個演算法,每一步的移動量都比BM演算法要大,所以肯定比BM演算法更快。#include<iostream> #include<fstream> #include<vector> #include<algorithm> #include<string> #include<list> #include<functional> using namespace std; int main() { char *text=new char[100]; text="substring searching algorithm search"; char *patt=new char[10]; patt="search"; size_t temp[256]; size_t *shift=temp; size_t patt_size=strlen(patt); cout<<"size : "<<patt_size<<endl; for(size_t i=0;i<256;i++) *(shift+i)=patt_size+1;//所有值賦於7,對這題而言 for(i=0;i<patt_size;i++) *(shift+unsigned char(*(patt+i) ) )=patt_size-i; /* // 移動3步-->shift['r']=6-3=3;移動三步 //shift['s']=6步,shitf['e']=5以此類推 */ size_t text_size=strlen(text); size_t limit=text_size-i+1; for(i=0;i<limit;i+=shift[text[i+patt_size] ] ) if(text[i]==*patt) { /* ^13--這個r是位,從0開始算 substring searching algorithm search searching-->這個s為第10位,從0開始算 如果第一個位元組匹配,那麼繼續匹配剩下的 */ char* match_text=text+i+1; size_t match_size=1; do{ if(match_size==patt_size) cout<<"the no is "<<i<<endl; }while( (*match_text++)==patt[match_size++] ); } cout<<endl; } delete []text; delete []patt; return 0; } //執行結果如下: /* size : 6 the no is 10 the no is 30 Press any key to continue */
