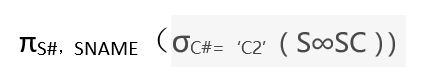【資料庫】關係代數基本運算
前言
關係代數是以關係為運算物件的一組高階運算的集合。由於關係定義為屬性個數相同的元組的集合,因此集合代數的操作就可以引入到關係代數中。關係代數中的操作可以分為兩類:傳統的關係操作,並、差、交、笛卡爾積(乘)、笛卡爾積的逆運算(除);擴充的關係操作,對關係進行垂直分割(投影)、水平分割(選擇)、關係的結合(連線、自然連線)等。
五個基本的關係代數操作
五個關係代數操作分別是:並、差、笛卡爾積、投影和選擇。
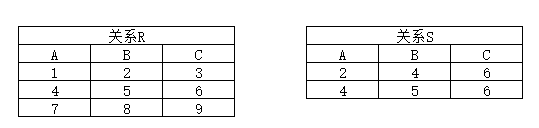
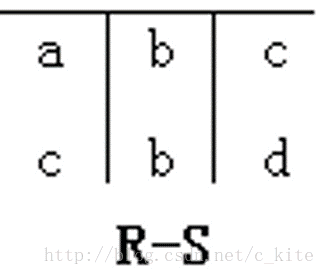
它們組成了關係代數完備的操作集。例子,分析下面兩個關係:
關係代數操作的結果
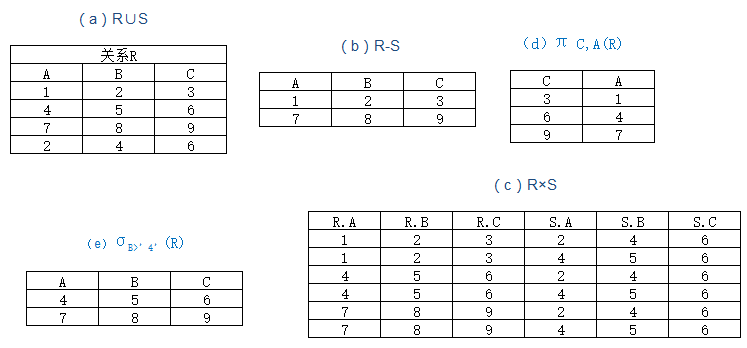
(a)R∪S 並 (b)R-S 差 (c)R×S 笛卡爾積 (d)πC,A(R) 投影 (e)σB>’4’ (R) 選擇
說明:笛卡爾積,若R有m個元組,S有n個元組,則R×S有m×n個元組。投影,C和A為屬性名,說明要選擇的列。選擇B>'4',即選擇語句的條件,對關係做水平分割,選擇符合條件的元組。
連線
連線是從關係R和S的笛卡爾積中選取屬性值滿足某一個操作的元組。
下面的例子同σ2=4 (R×S)。
自然連線
例項
在關係代數運算中,把由五個基本操作經過有限次複合的式子稱為關係代數表示式。這種表示式的運算結果仍是一個關係。我們可以用關係代數表示式表示各種資料查詢操作。
【例4.5】對於下面的教學資料庫中的四個關係,為方便起見,其名稱簡化為T、C、S和SC:
下面用關係代數表示式表達每個查詢語句
1)檢索學習課程號為C2課程的學生學號和姓名
由於這個查詢涉及到兩個關係S與SC,因此先要對這兩個關係進行自然連線操作,然後再執行選擇和投影操作。
《除法運算》:資料庫考試中經常會出現關係運算題目
而一般的加減乘運算相對比較簡單,通常不會直接出題
比較容易亂的是除法
認真看下面這段中的圖,很容易就理解出除法的
除法運算的定義:
這個概念的描述的非常抽象,剛開始學習的同學完全不知所云。這裡通過一個例項來說明除法運算的求解過程
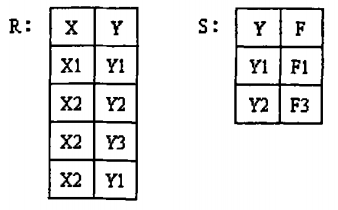
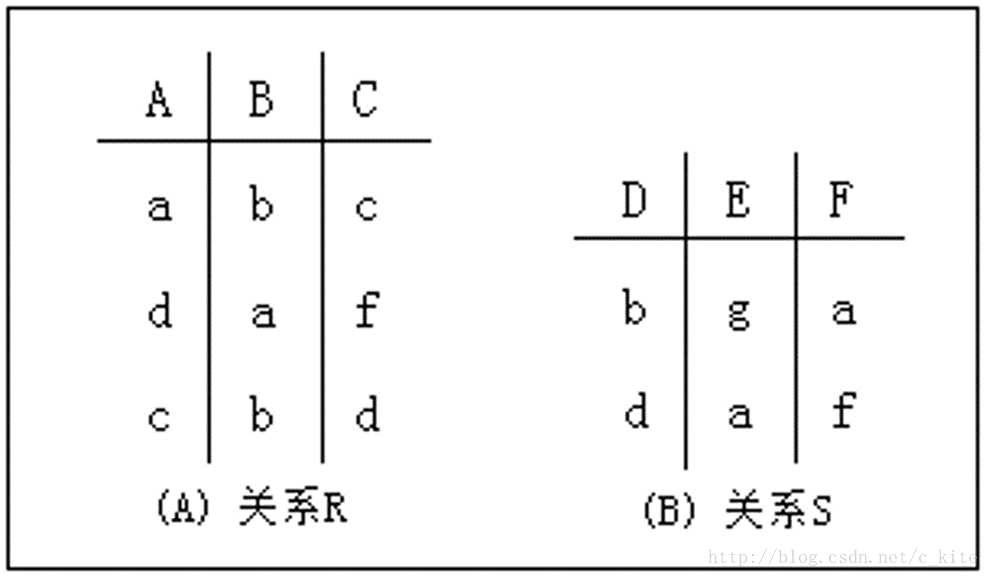
設有關係R、S 如圖所示,求R÷S 的結果
求解步驟過程:
第一步:找出關係R和關係S中相同的屬性,即Y屬性。在關係S中對Y做投影(即將Y列取出);所得結果如下
第二步:被除關係R中與S中不相同的屬性列是X ,關係R在屬性(X)上做取消重複值的投影為{X1,X2};
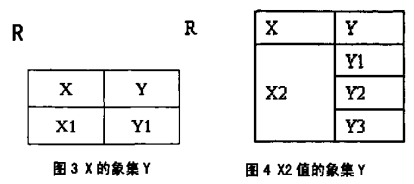
第三步:求關係R中X屬性對應的像集Y
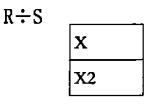
根據關係R的記錄,可以得到與X1值有關的記錄,如圖3所示;與X2有關的記錄,如圖4所示
第四步:判斷包含關係
R÷S其實就是判斷關係R中X各個值的像集Y是否包含關係S中屬性Y的所有值。對比即可發現:
X1的像集只有Y1,不能包含關係S中屬性Y的所有值,所以排除掉X1;
而X2的像集包含了關係S中屬性Y的所有值,所以R÷S的最終結果就是X2
差操作:
設R和S是n元關係,而且兩者各對應屬性的資料型別也相同。R和S的差定義為 R-S ={ t | t∈R∧tS}。
白話: 因為是R-S, 找R在S關係中沒有的