二分圖的最佳完美匹配

如果二分圖的每條邊都有一個權（可以是負數），要求一種完備匹配方案，使得所有匹配邊的權和最大，記做最佳完美匹配。（特殊的，當所有邊的權為1時，就是最大完備匹配問題）
我們使用KM演算法解決該問題。

KM（Kuhn and Munkres）演算法，是對匈牙利演算法的一種貪心擴充套件，如果對匈牙利演算法還不夠明白，建議先重新回顧一下匈牙利演算法。

KM是對匈牙利演算法的一種貪心擴充套件，這種貪心不是對邊的權值的貪心，演算法發明者引入了一些新的概念，從而完成了這種擴充套件。

可行頂標

對於原圖中的任意一個結點，給定一個函式L(node)求出結點的頂標值。我們用陣列l

x(x)記錄集合X中的結點頂標值，用陣列ly(y)記錄集合Y中的結點頂標值。
並且，對於原圖中任意一條邊edge(x,y),都滿足

lx(x)+ly(y)>=weight(x,y)

相等子圖

相等子圖是原圖的一個生成子圖（生成子圖即包含原圖的所有結點，但是不包含所有的邊）,並且該生成子圖中只包含滿足

lx(x)+ly(y)=weight(x,y)的邊,這樣的邊我們稱之為可行邊。

演算法原理

• 定理：如果原圖的一個相等子圖中包含完備匹配，那麼這個匹配就是原圖的最佳二分圖匹配。

• 證明 ：由於演算法中一直保持頂標的可行性，所以任意一個匹配的權值之和肯定小於等於所有結點的頂標之和，則相等子圖中的完備匹配肯定是最優匹配。

這就是為什麼我們要引入可行頂標和相等子圖的概念。
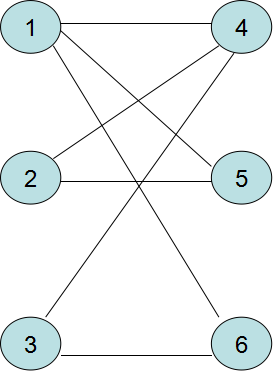
上面的證明可能太過抽象，我們結合圖示更直觀的表述。

該圖表示原圖，且X=1,2,3,Y=4,5,6,給出權值

weight(1,4)=5
weight(1,5)=10
weight(1,6)=15
weight(2,4)=5
weight(2,5)=10
weight(3,4)=10
weight(3,6)=20

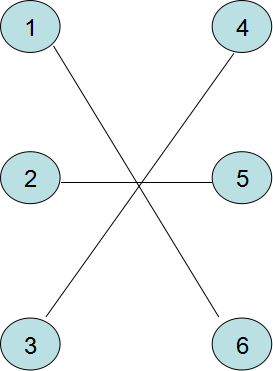
對於原圖的任意一個匹配M

那麼對於

edge(1,6)weight(1,6)=15
edge(2,5)weight(2,5)=10
edge(3,4)weight(3,4)=10

都滿足

lx(x)+ly

(y)>=weight(x,y)

所以

∑i=1xi∈Xlx(xi)+∑i=1yi∈Yly(yi)=K>=∑weight(xi,yi)

可以看出，一個匹配中的邊權之和最大為K。

那麼很顯然，當一個匹配G∗的邊權之和恰好為K時，那麼G∗就是二分圖的最佳完美匹配。

如果對於每一條邊edge(xi,yi)都滿足

lx(xi)+ly(yi)==weight(xi,yi)
那麼∑i=1xi∈Xlx(xi)+∑i=1yi∈Yly(yi)=K=∑weight(xi,yi)

相等子圖的完備匹配（完美匹配）即滿足上述條件（因為相等子圖的每條邊都是可行邊，可行邊滿足