首先，我們從一道題來引出這個問題。

假如已知有n個人和m對好友關係（存於數字r）。如果兩個人是直接或間接的好友（好友的好友的好友…），則認為他們屬於同一個朋友圈，請寫程式求出這n個人裡一共有多少個朋友圈。假如：n = 5，m = 3，r = {{1 , 2} , {2 , 3} , {4 , 5}}，表示有5個人，1和2是好友，2和3是好友，4和5是好友，則1、2、3屬於一個朋友圈，4、5屬於另一個朋友圈，結果為2個朋友圈。

這道題解決它的辦法就是利用並查集。

並查集是一種簡單的集合，它支援 Union（把第二個子集合併入第一個集合）。注意只有兩個集合不相交的時候才能並集。然後是Find，它用來搜尋集合所給元素所在集合，然後返回集合的名字。

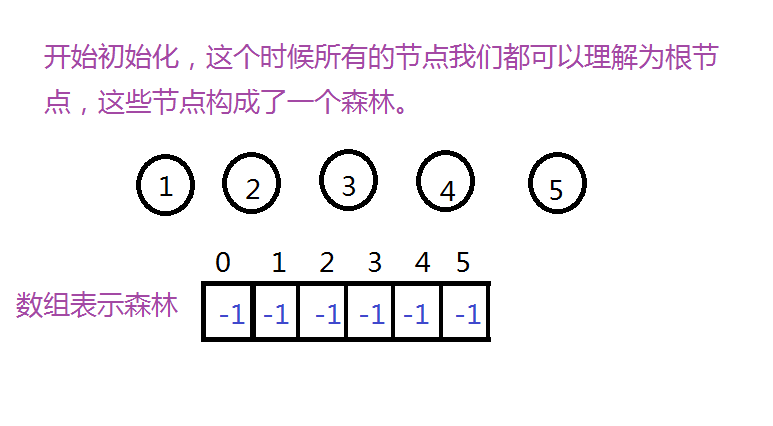
實現並查集：並查集的實現可以理解成森林。每一個集合是一棵樹。在這裡我們用可以用一個數組來表示，元素對應陣列的下標，而根節點的內容我們認為都是-1。所以，預設的整個陣列數值都為-1。所以我們初始化就是：

當初始化完以後，我們就進行合併操作來解決。然後我們進行Union的操作。

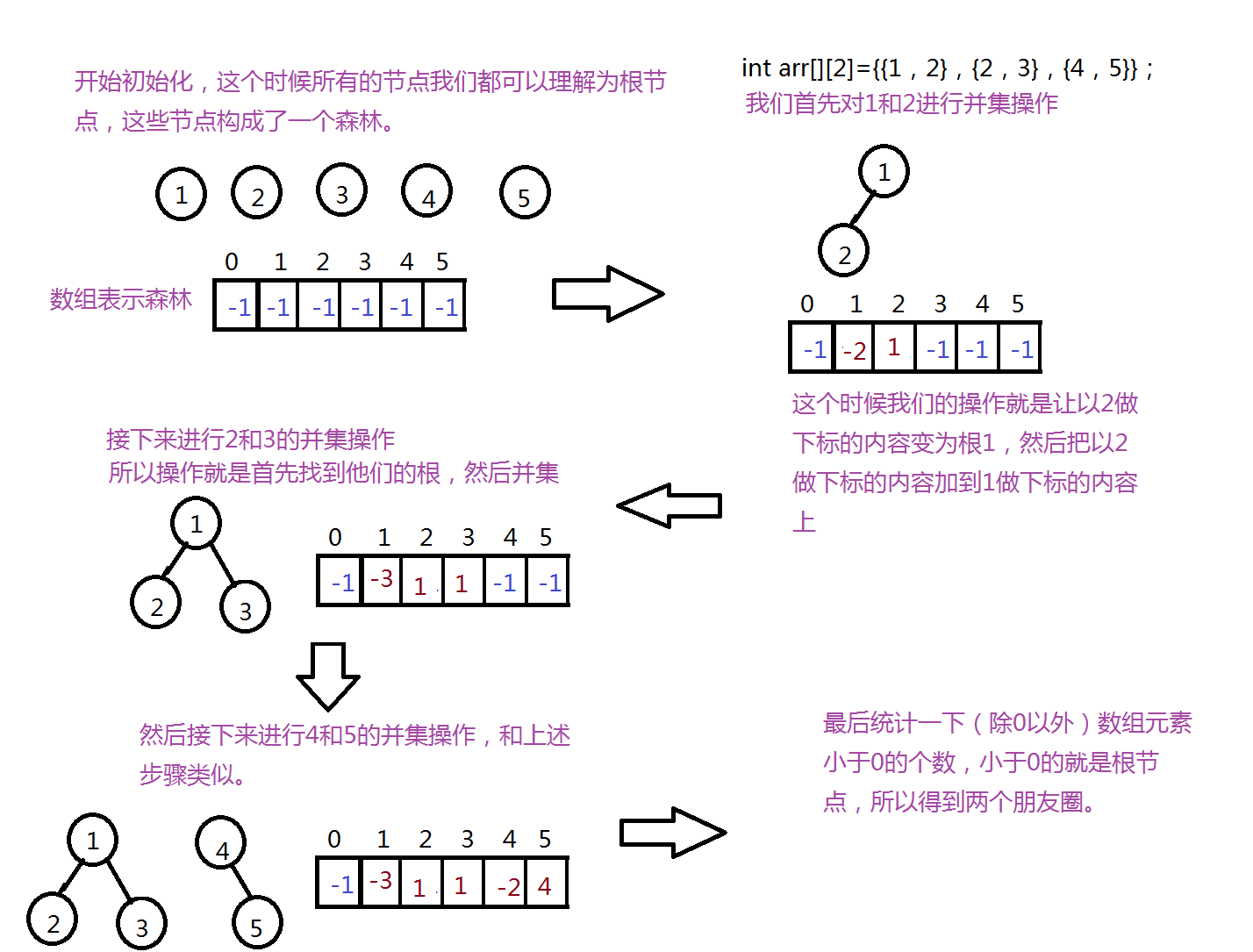
Union（root1，root2）是把root2作為子集併入root1中，簡單說就是找出root2的這棵樹，併入root1，操作也就是把root2的根連到root1的根下。
所以，在這裡我們要並的時候，首先要找root1和root2的根，然後找到根以後，對它們的根進行並的操作。
我們就拿上面那道題作為例子來畫圖說明。

程式碼實現：

class UnionSet
{
public:
    UnionSet(int n)
        :_size(n + 1)
    {
        //開闢一個數組，這個陣列全為-1，因為是-1.所以使用memset就可以了，否則，考慮for迴圈
        _parent = new int[n + 1];
        memset(_parent, -1, sizeof(int)*(n + 1));

    }
    ~UnionSet()
    {
        delete[] _parent;
    }
    //合併並查集
    void
 
 Union(int r1, int r2)
    {
        //得到兩個並查集的根
        int root1 = Find(r1);
        int root2 = Find(r2);
        //把第二個並查集加到第一個上，把父節點放到內容。
        if (root1 != root2)
        {
            _parent[root1] += _parent[root2];
            _parent[root2] = root1;
        }
    }
    int Find(int index)
    {
        int root = index;
        while (_parent[root] >= 0)
        {
            root = _parent[root];
        }
        return root;
    }

    int CountRoot()
    {
        int count = 0;
        for (int i = 1; i < _size; i++)
        {
            if (_parent[i] <0)
                count++;
        }
        return count;
    }
protected:
    int *_parent;
    int _size;
};
int friends(int n, int m, int arr[][2])
{
    UnionSet a(n);
    for (int i = 0; i < m; i++)
    {
        a.Union(arr[i][0], arr[i][1]);
    }
    int rootcount = a.CountRoot();
    return rootcount;
}
void test1()
{
    int n = 3;
    int m = 5;
    int arr[][2] = { { 1, 2 }, { 2, 3 }, { 4, 5 } };

    int count = friends(n,m, arr);
}