盤點機器學習中常見的損失函式和優化演算法
阿新 • • 發佈:2019-01-10
在機器學習中,對於目標函式、損失函式、代價函式等不同書上有不同的定義。通常來講,目標函式可以衡量一個模型的好壞,對於模型的優化通常求解模型的最大化或者最小化,當求取最小化時也稱loss function即損失函式,也稱為成本函式、代價函式。 大多數情況下兩者並不做嚴格區分。損失函式包含損失項與正則項。正則項的目的是提高模型的泛化能力,防止過擬合。本文僅討論損失項,下面是一些常見的損失函式的損失項。
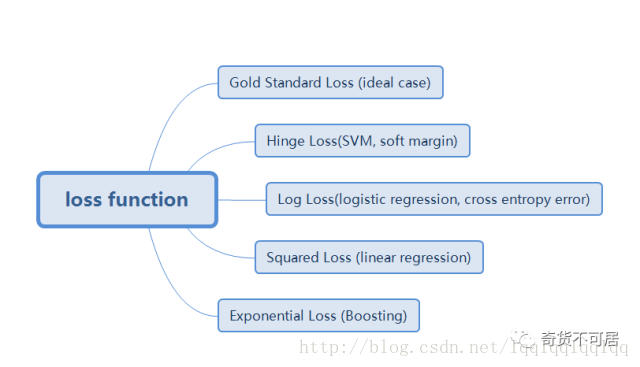
1.Gold Standard Loss
又被稱為0-1 loss, 記錄分類錯誤的次數。
2.Hinge Loss
最常用在 SVM 中的最大化間隔分類中。對可能的輸出 t = ±1和分類器分數y,預測值 y 的 hinge loss 定義如下: L(y) = max(0,1-t*y) 對於hinge loss,又可以細分出hinge loss(或簡稱L1 loss)和squared hinge loss(或簡稱L2 loss)(注意與正則化有區別)。
3.Log Loss對數損失
對於對數函式,由於其具有單調性,在求最優化問題時,結果與原始目標一致,在含有乘積的目標函式中(如極大似然函式),通過取對數可以轉化為求和的形式,從而大大簡化目標函式的求解過程。
此外,由於log函式是單調遞增,為了轉化為最小化問題,通常新增負號,即通常所說的negative log function.
4.Squared Loss 平方損失
即真實值與預測值之差的平方和。通常用於線性模型中,如線性迴歸模型。之所以採用平方的形式,而非絕對值或三次方的形式,是因為極大似然與最小化平方損失是等價的,具體推導可以參考https://zhuanlan.zhihu.com/p/26171777。
5.Exponential Loss 指數損失
指數函式具有單調性,非負性的優良性質,使得越接近正確結果誤差越小,Adaboost演算法即使用的指數損失目標函式。但是指數損失存在的一個問題是誤分類樣本的權重會指數上升,如果資料樣本是異常點,會極大的干擾後面基本分類器學習效果,這也是Adaboost演算法的一個缺點。
此外還有絕對值損失,通常用於迴歸中。
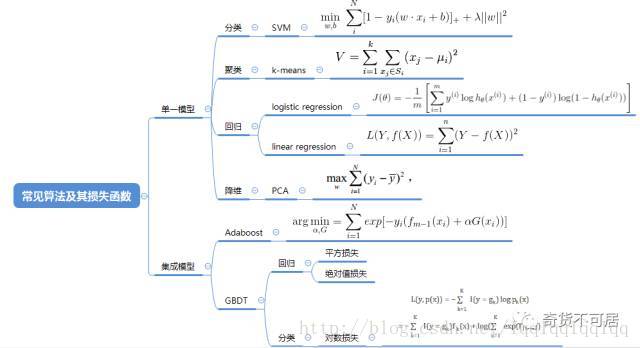
下面是機器學習中常見演算法的損失函式。如果需要詳細瞭解背後的原理,可以查閱相關資料。
值得注意的是,上述目標函式中許多沒有解析解,對於此類問題,我們通常可以採取一些迭代的演算法來解決。下面是一些常見的優化演算法。
總結:
本文盤點了機器學習中常見的目標函式(損失函式)損失項的形式,以及常見演算法的目標函式具體形式,最後給出了常見的優化演算法及其優缺點。值得注意的是,本文並不代表全部的總結,如有疏漏及錯誤之處,歡迎指正!
轉載請註明出處。歡迎關注本公眾號,檢視更多幹貨!