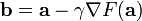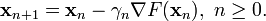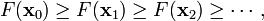梯度下降法是機器學習和神經網路學科中我們最早接觸的演算法之一。但是對於初學者，我們對於這個演算法是如何迭代執行的從而達到目的有些迷惑。在這裡給出我對這個演算法的幾何理解，有不對的地方請批評指正！

        梯度下降法定義

        （維基百科）梯度下降法，基於這樣的觀察：如果實值函式在點處可微且有定義，那麼函式在點沿著梯度相反的方向下降最快。

        因而，如果

        對於為一個夠小數值時成立，那麼。

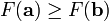        考慮到這一點，我們可以從函式的區域性極小值的初始估計出發，並考慮如下序列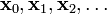

        因此可得到

       如果順利的話序列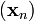收斂到期望的極值。注意每次迭代步長可以改變。

        下面圖片示例了這一過程，這裡假設定義在平面上，並且函式影象是一個碗形。藍色的曲線是等高線(水平集)，即函式為常數的集合構成的曲線。紅色的箭頭指向該點梯度的反方向。（一點處的梯度方向與通過該點的等高線垂直）。沿著梯度下降方向，將最終到達碗底，即函式值最小的點。

梯度下降法幾何解釋：

       由於我們的任務是求得經驗損失函式的最小值，所以上圖的過程實際上是一個“下坡”的過程。在每一個點上，我們希望往下走一步（假設一步為固定值0.5米），使得下降的高度最大，那麼我們就要選擇坡度變化率最大的方向往下走，這個方向就是經驗損失函式在這一點梯度的反方向。每走一步，我們都要重新計算函式在當前點的梯度，然後選擇梯度的反方向作為走下去的方向。隨著每一步迭代，梯度不斷地減小，到最後減小為零。這就是為什麼叫“梯度下降法”。

       那麼，為什麼梯度的方向剛好是我們下坡的反方向呢？為什麼我們不是沿著梯度的方向下坡呢？這是因為，只有沿著梯度的反方向，我們才能下坡，否則就是上坡了……舉個例子，在y=f（x）的二維平面上，規定好x軸和y軸的方向後，如果曲線f（x）的值是隨著x的增加上升的，那麼它在某一點的切線的數值一定是正的。反之，若曲線f（x）的值是隨著x的增加下降的，則它在下降的某一點的切線的數值一定是負數。梯度是方向導數在某一點的最大值，所以其值必然是正數。如果沿著梯度方向走，經驗損失函式的值是增加的……所以，我們要下坡，就必須沿著梯度方向的反方向了。

梯度上升法幾何解釋：

       相對於梯度下降法，還有梯度上升法。（注意減號變成加號了）

       其基本原理與下降法一致，區別在於：梯度上升法是求函式的區域性最大值。因此，對比梯度下降法，其幾何意義和很好理解，那就是：演算法的迭代過程是一個“上坡”的過程，每一步選擇坡度變化率最大的方向往上走，這個方向就是函式在這一點梯度方向（注意不是反方向了）。最後隨著迭代的進行，梯度還是不斷減小，最後趨近與零。

       有一點我是這樣認為的：所謂的梯度“上升”和“下降”，一方面指的是你要計算的結果是函式的極大值還是極小值。計算極小值，就用梯度下降，計算極大值，就是梯度上升；另一方面，運用上升法的時候引數是不斷增加的，下降法是引數是不斷減小的。但是，在這個過程中，“梯度”本身都是下降的。

       注：這裡的梯度減小指的是梯度的數值大小，不包含方向的正負號。