第一次寫部落格，好激動啊，哈哈。之前看了許多東西但經常是當時花了好大功夫懂了，但過一陣子卻又忘了。現在終於決定追隨大牛們的腳步，試著把學到的東西總結出來，一方面梳理思路，另一方面也作為備忘。接觸機器學習不久，很多東西理解的也不深，文章中難免會有不準確和疏漏的地方，在這裡和大家交流，還望各位不吝賜教。
　　先從基礎的開始寫起吧。這是學習Andrew Ng的課程過程中的一些筆記，慢慢總結出來和大家交流。
　　（又加了一部分代價函式的概率解釋——2016.4.10）

房價預測問題

　　還是經典的預測房價的例子。假如我們收集了這麼一組資料，描述了某一地區房子大小與價格的資訊：

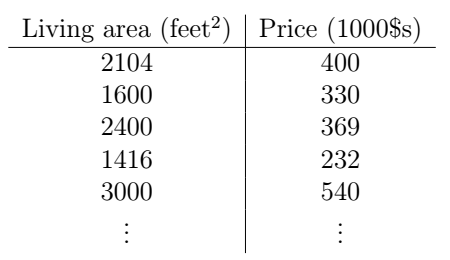
　　我們把它在座標系中畫出來，就是這個樣子：

　　好了，現在問題來了，如今樓市價格突飛猛進，而你剛剛蒐集了一些這個地區其它房子的面積資訊，並想要以此預測一下它們的價格，你該怎麼做？
　　為了表述清晰，我們先來約定一下符號表示。我們用x(i)表示輸入變數（也就是房子的大小），這也被稱作特徵。y(i)表示輸出，或者叫目標變數，也就是我們想要預測的變數（價格）。這麼一對輸入輸出(x(i),y(i))被稱作訓練樣本，我們用來學習預測方法的資料集包含了m個訓練樣本，它們被稱作訓練集。注意，這裡的上標(i)與冪沒有半毛錢關係，它只是代表了訓練集中樣本的編號或索引（index）。
　　我們用X和Y分別表示輸入和輸出的變數空間。在上面的房價預測問題中，輸入和輸出變數都是一維的，因此我們有X

=Y=R。
　　好了，說完這些繁瑣的符號，我們回到房價預測的問題上。我們來理一下思路，為了能夠對一個新的樣本進行預測，我們首先要從已有的樣本中發現其中的“規律”，然後把這個“規律”應用到新的樣本中，我們就可以得到一個預測。好了，我們的目標就很明確了，我們首先要根據訓練集學習一個函式h:X→Y，它把輸入變數從空間X對映到空間Y，得到輸出變數。由於歷史的原因，人們常常把函式h稱為假設（hypothesis）。這裡，我們的訓練樣本都是有標籤的，也就是我們的訓練樣本包含了x和y，這被稱為有監督學習。還有另外一種情況，訓練樣本是無標籤的，也就是隻包含x，被稱為無監督學習。下面這張圖說明了我們的預測流程：
　　
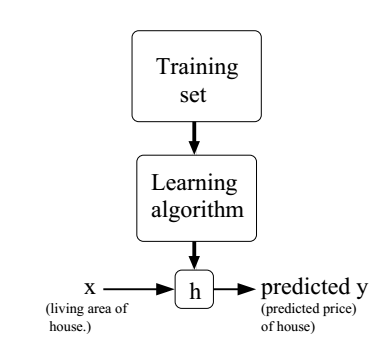
　　如果我們要預測的變數是連續的，就像上面的房價問題，那麼我們稱這種學習問題為迴歸（regression）問題，如果是離散的（比如我們想要預測這是一個別墅還是公寓），那就被稱為分類（classification）問題。

線性迴歸

　　實際上我們收集到的房子的特徵可能不止一個，假設我們又收集到了有關房屋臥室數量的資訊，顯然這也會對房子的價格有影響。好，我們的表格就變成了這樣：
　　
　　現在，x就是一個二維的向量了，x∈R2. 現在，我們假設函式h是x的線性函式：
　　　　　　　　　　(1)
　　
　　θi是線性函式的引數（也叫權值），大家發現上式多了一項θ0，它是x0的係數，我們習慣上令x0=1，這被稱為截距項。上式寫為向量形式：
　　　　　　　　　　　　(2)
　　
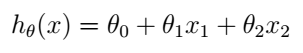
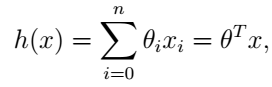
　　這裡我們省略了h的下標θ。

梯度下降法

　　有了線性模型，我們現在的任務就是想辦法求出h(x)，也就是求出引數θ。我們對假設函式h(x)有什麼要求呢？當然是希望它能儘量準確地預測出y的值。換句話說，對於訓練集中的樣本，我們希望選取的θ滿足使h(x)的輸出與y的距離儘可能地小。於是我們可以定義如下的代價函式：
　　　　　　(3)
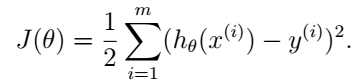
　　注意，這個代價函式是θ的函式，因為我們現在的任務是尋找θ，使預測誤差最小。
那我們怎麼才能找到使J(θ)最小的θ呢？想象一下，如果你站在一個山谷的某個坡上，你怎樣才能最快到達山谷的谷底呢？當然是沿山坡下降最快的方向走下去。對！我們的最小化J(θ)的思路和這簡直一毛一樣！我們首先隨機初始化θ的值，也就是我們先猜θ的值，對不對沒關係，反正都是猜的，然後我們一步步地向使J(θ)最小的方向更新。使J(θ)最小的方向是什麼？當然是它的梯度的反方向啊！好了，現在目標已經很明確了，我們要做的就是這樣：
　　　　　　　　　　　　　(4)
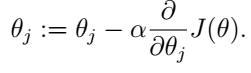
　　注意，這裡的:=是賦值的意思。這個更新過程要對每一個j都過一遍。α是學習速率，它表示你每一步更新的幅度有多大，就相當於你下山時每一步邁多大一樣。好，我們現在來求等式右邊的梯度吧。為了簡便起見，我們先考慮只有一個訓練樣本的情況，這樣我們就可以省略式(3)中的求和符號了：
　　　　　(5)
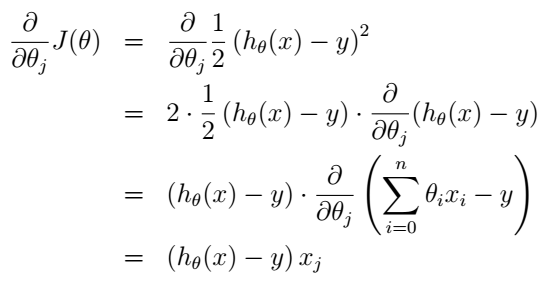
　　把式(5)代入式(4)我們就得到了更新規則：
　　　　　(6)
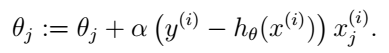
　　這個規則稱為LMS更新規則(least mean squares)，或者叫Widrow-Hoff learning rule。這個規則看起來也很直觀：如果假設和樣本偏差很小時我們就更新地幅度小一點，反之更新地幅度就大一點。
　　上面的LMS規則是針對單個樣本的，我們有兩種方法把它擴充套件到多個訓練樣本。一種是直接把單個樣本代價函式的梯度換為多個樣本代價函式的梯度。由於多個樣本的代價函式是單個樣本代價函式的線性加和，所以其梯度也是單個樣本代價函式的梯度的加和，我們把它替換之後就得到如下演算法：
　　
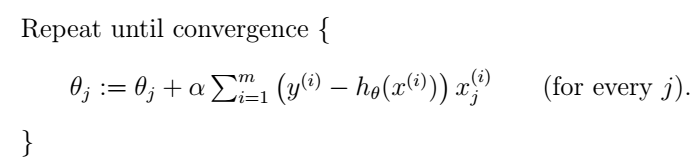
　　這種方法每次更新都遍歷訓練集中所有的樣本，以它們的預測誤差之和為依據更新，所以被稱為batch gradient descent。其實梯度下降法是有可能收斂於一個區域性最小值的，但是我們這裡的線性迴歸問題只有一個全域性最優解，不存在區域性最小值，所以如果學習速率α不是過大，梯度下降法總是能夠收斂。實際上，J(θ)是一個凸的平方函式。
　　上面講的是batch gradient descent，還有另外一種梯度下降演算法，效果也很好，叫做stochastic gradient descent (也叫incremental gradient descent)，如下：
　　
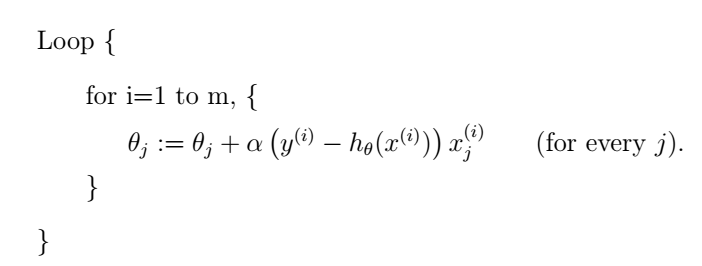
　　這種方法中我們同樣也要遍歷整個訓練集，但和batch gradient descent不同的是，我們每次只使用單個訓練樣本來更新α，依次遍歷訓練集，而不是一次更新中考慮所有的樣本。當訓練樣本數m很大時，batch gradient descent的每次更新都會是計算量很大的操作，而stochastic gradient descent 可以利用單個訓練樣本立即更新，因此stochastic gradient descent 通常是一個更快的方法。但stochastic gradient descent 也有一個缺點，那就是它的α可能不會收斂於最小值，而是在最小值附近振盪，但在實際中也都會得到一個足夠好的近似。或者更通常的情況是，我們不用固定的學習速率，而是讓它隨著演算法的執行逐漸減小到零，也就是在接近“谷底”的時候慢慢減小下降的“步幅”，換成用“小碎步”走，這樣它就更容易收斂於全域性最小值而不是圍繞它振盪了。基於這些原因，特別是當訓練集很大時，人們更加傾向於使用stochastic gradient descent。

代價函式的概率解釋

　　現在我們來討論一下為什麼我們選擇這樣的代價函式J。線性迴歸的代價函式看起來非常直觀：我們希望最小化預測值與訓練集中實際值之差的平方。這裡面其實也是可以從概率的角度來解釋的。
　　我們首先假設目標變數和輸入之間有這樣的關係：
　　

y(i)=θTxi+ϵ(i)
　　ϵ(i)代表了沒有被線性模型捕捉到的一些因素的影響，比如一些我們沒有發現的影響房價的潛在特徵啊，隨機噪聲啊（甚至是賣房子的人當時開不開心啊（哈哈，不要在意這些細節））。我們假設ϵ(i)是獨立同分布的（independently and identically distributed，IID），它們符合高斯分佈（Gaussian distribution）（也叫正態分佈，Normal distribution），寫作ϵ(i)∼N(0,σ2)，其中σ2是方差，均值為零，它的密度函式為：
p(ϵ(i))=12π−−√σexp(−ϵ(i)2σ2).
注意，這個ϵ代表了y和x的線性模型之間的差，它符合高斯分佈，也就是說線上性模型（由引數θ控制）確定的情況下，給定x(i)，y(i)的條件分佈是這樣的：
p(y(i)|(x(i);θ)=12π−−√σexp(−(y(i)−

相關推薦

吳恩達深度學習筆記（8）-重點-梯度下降法（Gradient Descent）

梯度下降法（Gradient Descent）（重點） 梯度下降法可以做什麼？ 在你測試集上，通過最小化代價函式（成本函式） J(w,b) 來訓練的引數w和b ， 如圖，在第二行給出和之前一樣的邏輯迴歸演算法的代價函式（成本函式）(上一篇文章已講過） 梯度下降法的形象化

高斯混合模型（GMM model）以及梯度下降法（gradient descent）更新引數

關於GMM模型的資料和 EM 引數估算的資料，網上已經有很多了，今天想談的是GMM的協方差矩陣的分析、GMM的引數更新方法 1、GMM協方差矩陣的物理含義 涉及到每個元素，是這樣求算： 用中文來描述就是： 注意後面的那個除以（樣本數-1），就是大括號外面的E求期望　（這叫

梯度下降法（Gradient Descent）

　　第一次寫部落格，好激動啊，哈哈。之前看了許多東西但經常是當時花了好大功夫懂了，但過一陣子卻又忘了。現在終於決定追隨大牛們的腳步，試著把學到的東西總結出來，一方面梳理思路，另一方面也作為備忘。接觸機器學習不久，很多東西理解的也不深，文章中難免會有不準確和疏漏的

機器學習與高數：梯度（Gradient）與梯度下降法（Gradient Descent）

一篇經典部落格： http://blog.csdn.net/walilk/article/details/50978864 1.導數定義：導數代表了在自變數變化趨於無窮小的時候，函式值的變化與自變數的變化的比值。幾何意義是這個點的切線。物理意義是該時刻的（瞬時）變化率。

梯度下降演算法（Gradient descent）

梯度下降演算法是一種求區域性最優解的方法，在wikipedia上對它做了詳細的說明，這裡我只是把自己感興趣的一些地方總結一下： 對於F(x)，在a點的梯度是F(x)增長最快的方向，那麼它的相反方向則是該點下降最快的方向，我們有如下結論： 其中，v是一個大於0的數，於是我們

梯度下降算法（gradient descent）

調整 none 算法 方向導數 分享圖片 後繼 常用 也有 計算 簡述梯度下降法又被稱為最速下降法(Steepest descend method)，其理論基礎是梯度的概念。梯度與方向導數的關系為：梯度的方向與取得最大方向導數值的方向一致，而梯度的模就是函數在該點的方向導數

批梯度下降法(Batch Gradient Descent )，小批梯度下降 (Mini-Batch GD)，隨機梯度下降 (Stochastic GD)

一、梯度下降法 　　在機器學習演算法中，對於很多監督學習模型，需要對原始的模型構建損失函式，接下來便是通過優化演算法對損失函式進行優化，以便尋找到最優的引數。在求解機器學習引數的優化演算法中，使用較多的是基於梯度下降的優化演算法(Gradient Descen

斯坦福大學機器學習筆記——單變數的線性迴歸以及損失函式和梯度下降法（包含程式碼）

迴歸問題： 所謂的迴歸問題就是給定的資料集，且每個資料集中的每個樣例都有其正確的答案，通過給定的資料集進行擬合，找到一條能夠最好代表該資料集的曲線，然後對於給定的一個樣本，能夠預測出該樣本的答案（對於迴歸問題來說，最終的輸出結果是一個連續的數值）。比如

批量梯度下降法（Batch Gradient Descent）

所有 margin 初始 ont 模型 log eight 梯度下降 img 批量梯度下降：在梯度下降的每一步中都用到了所有的訓練樣本。 思想：找能使代價函數減小最大的下降方向（梯度方向）。 　　　　ΔΘ = - α▽J α：學習速率 梯度下降的線性回歸 　　

隨機梯度下降法（Stochastic Gradient Descent）和批量梯度下降法（Batch Gradient Descent ）總結

梯度下降法常用於最小化風險函式或者損失函式，分為隨機梯度下降（Stochastic Gradient Descent）和 批量梯度下降（Batch Gradient Descent ）。除此之外，還有梯度上升法（Gradient Ascent），應用於極大似

學習筆記13：隨機梯度下降法（Stochastic gradient descent, SGD）

假設我們提供了這樣的資料樣本（樣本值取自於y=3*x1+4*x2）：x1x2y1419252651194229x1和x2是樣本值，y是預測目標，我們需要以一條直線來擬合上面的資料，待擬合的函式如下：我們

機器學習筆記——梯度下降（Gradient Descent）

梯度下降演算法（Gradient Descent） 在所有的機器學習演算法中，並不是每一個演算法都能像之前的線性迴歸演算法一樣直接通過數學推導就可以得到一個具體的計算公式，而再更多的時候我們是通過基於搜尋的方式來求得最優解的，這也是梯度下降法所存在的意義。 不是一個機器學習演

機器學習1：梯度下降（Gradient Descent）

分別求解損失函式L(w,b)對w和b的偏導數，對於w，當偏導數絕對值較大時，w取值移動較大，反之較小，通過不斷迭代，在偏導數絕對值接近於0時，移動值也趨近於0，相應的最小值被找到。 η選取一個常數引數，前面的負號表示偏導數為負數時（即梯度下降時），w向增大的地方移動。 對於非單調函式，

機器學習3- 梯度下降（Gradient Descent）

1、梯度下降用於求解無約束優化問題，對於凸問題可以有效求解最優解 2、梯度下降演算法很簡單就不一一列，其迭代公式： 3、梯度下降分類（BGD，SGD，MBGD） 3.1 批量梯度下降法（Batch Gradient Descent） 　　　　批量梯度下降法，是梯度

【吳恩達機器學習筆記】005 梯度下降（Gradient Descent）

一、引入        在前幾節課我們講到，我們希望能夠找到曲線擬合效果最好的線條，這樣的線條的誤差最小，所以就轉化成了下面這幅圖所表達的內容。        我們有一些函式，這些函式會有n個引數，我們希望能得到這個函式的最小值，為了方便計算，我們從最簡單的入手，讓引數的個數

機器學習(7)--梯度下降法（GradientDescent）的簡單實現

曾經在  機器學習(1)--神經網路初探  詳細介紹了神經網路基本的演算法，在該文中有一句weights[i] += 0.2 * layer.T.dot(delta) #0.2學習效率，應該是一個小於0.5的數，同時在  tensorflow例項(2)--機器學習初試

梯度下降法（上升法）的幾何解釋

             梯度下降法是機器學習和神經網路學科中我們最早接觸的演算法之一。但是對於初學者，我們對於這個演算法是如何迭代執行的從而達到目的有些迷惑。在這裡給出我對這個演算法的幾何理解，有不

機器學習金典演算法（二）--梯度下降法（2）

機器學習金典演算法（二）–梯度下降法        本人上篇博文梯度下降法（1）解釋了梯度下降法在機器學習中位置及思想，本文將繼續討論梯度下降法，梯度下降法存在的問題及改進思路，以及現有的幾種流行的變種梯度下降法。 目錄

梯度下降法（GD,SGD,Mini-Batch GD）線上性迴歸中的使用

https://github.com/crystal30/SGDLinrearRegression一.  梯度下降法(Batch Gradient Descent)1.梯度下降法的原理(1)   梯度下降法是一種基於搜尋的最優化方法，不是一個機器學習演算法。(2)   作用：

（3）梯度下降法Gradient Descent

作用 http 方程 優化方法 radi 方法 分享 移動 最優解 梯度下降法 不是一個機器學習算法 是一種基於搜索的最優化方法 作用：最小化一個損失函數 梯度上升法：最大化一個效用函數 舉個栗子 直線方程：導數代表斜率 曲線方程：導數代表切線斜率 導數可以代表方