1）平移變換

從一個位置到另一個位置的變換可以用平移矩陣T表示，該矩陣通過向量t=(t_x,t_y,t_z)對實體進行平移操作。

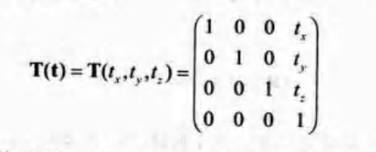其實還有另外一種形式（以左手座標系為基準）：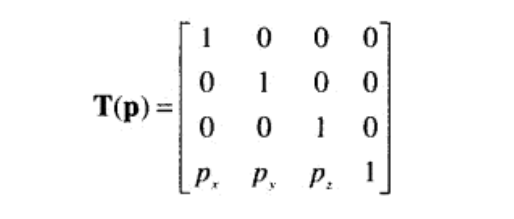

第一種形式（以右手座標系為基準的）進行變換時將T與需要變換的點或向量A（列向量）相乘，即TA。第二種形式（以左手座標系為基準）將需要變換的點或向量（行向量）與T相乘，即AT。

平移矩陣的逆矩陣為T^-1(t)= T(-t)，也就是對向量t進行了置負操作。

2）旋轉變換

旋轉矩陣 R_x(Θ)、R_y(Θ)、R_z(Θ)分別表示將物體繞x,y,z軸進行旋轉。

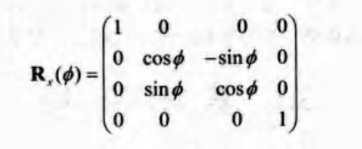
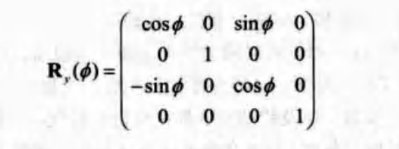
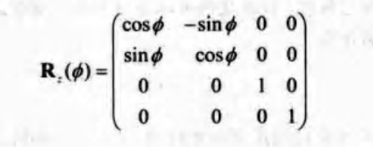
注意，旋轉矩陣表示物體是繞著指定軸（軸的指向朝外面）按順時針方向旋轉的，但這個形式的旋轉矩陣是以右手座標系

左手座標系的為：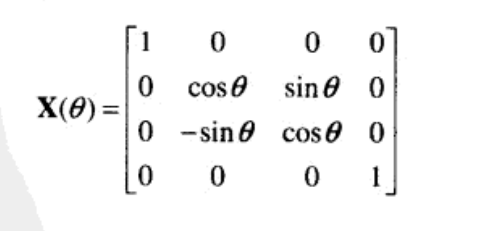

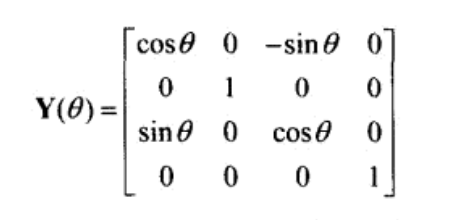
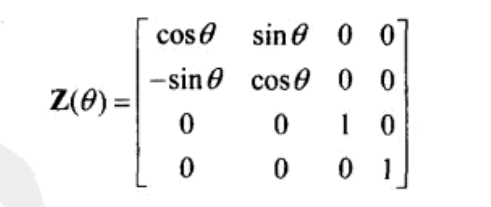
旋轉矩陣的推導可以看這裡：http://blog.csdn.net/zsq306650083/article/details/8773996

任意軸旋轉任意角度矩陣：

對於這個3x3矩陣來說，其對角元素之和是一個與座標軸無關的常數，稱其為跡（Trace）：tr(R) = 1+2cosΘ

矩陣R的逆矩陣就是其轉置矩陣，還有其他獲取其逆矩陣的方法，即將Θ取負（繞著同一 座標軸朝相反方向旋轉）。旋轉矩陣的行列式總是等於1.

3）縮放矩陣

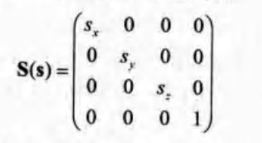    s_x,s_y,s_z分別表示沿著XYZ軸進行縮放的縮放比例。S矩陣的逆矩陣為S^-1(s) = S(1/s_x,1/s_y,1/s_z)。

如果對縮放矩陣s的一個或者三個分量置負，就會產生一個反射矩陣（映象矩陣），如果其中兩個縮放因子為-1，那麼將旋轉180度，當發現變換矩陣是反射矩陣時，需要進行特殊處理，例如，一個三角形的頂點序列以逆時針方向排列時，在經過反射矩陣變換後，對得到一個順時針方向排列的三角形頂點序列，這將導致不正確的光照效果和背面裁減。判斷給點矩陣是否為反射形式，需要計算該矩陣左上部3x3矩陣行列式的值，如果為負，那麼該矩陣就為反射矩陣。

4）錯切變換

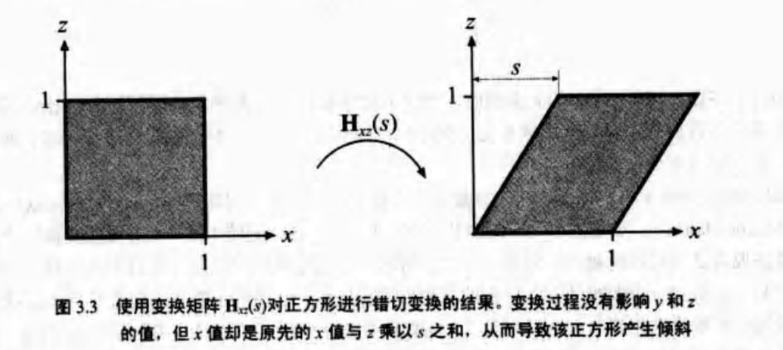
錯切矩陣有6種基本形式，分別表示為H_xy(s)、H_xz(s)、H_yx(s)、H_yz(s)、H_zx(s)、H_zy(s). 第一個下標表示由錯切矩陣改變的座標，第二個下標表示進行錯切操作的座標。

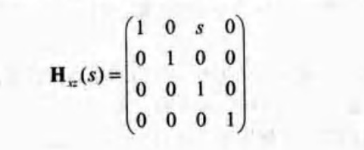  通過下標可以找到引數s所在的位置。如本例中x=0,z=2。

    錯切矩陣的逆矩陣可以通過取負來取得 (H_ij)^-1(s)= H_ij(-s)

5) 剛體變換

剛體變換用於剛性物體的變換，只改變物體的方向和位置，不改變形狀。可以將剛體矩陣X寫成一個平移矩陣和一個旋轉矩陣的級聯：

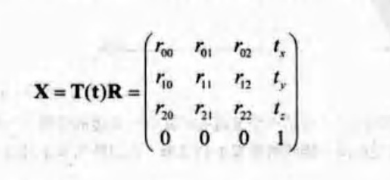
X的逆矩陣可以這樣求得：X^-1=(T(t)R)^-1=R^-1T(t)^-1=R^TT(-t).

6) 法線變換

注意，法線必須通過用變換幾何圖形的矩陣的逆矩陣的轉置矩陣進行變換 N=(M^-1)^T

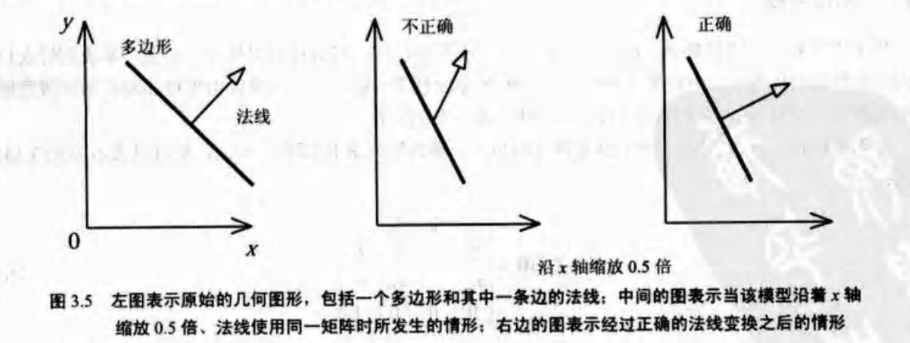
實際應用中，如果變換矩陣是正交的（如旋轉矩陣），就沒必要計算它的逆矩陣，因為正交矩陣的逆矩陣就是轉置矩陣，兩個轉置矩陣相互抵消，相乘的結果還是原來的旋轉矩陣。此外，還有平移矩陣，由於平移不改變向量的方向，所以可以進行任意次數的平移而不對法線產生任何影響。另外，如果使用一個或多個一致性縮放矩陣進行變換，也不需要計算相應的逆矩陣，因為這種縮放只改變法線長度，不影響其方向。這種矩陣進行變換之後需要對法線進行歸一化（規範化）。