計算機圖形學（四）_幾何變換_1_基本的二維幾何變換(一)
阿新 • • 發佈：2019-01-09
4 .幾何變換
使用線段和填充區等圖元來描述場景，並利用屬性來輔助這些圖元。我們給出了掃描線演算法，可以將圖元顯示在光柵裝置上。現在，再看看可用於物件重定位或改變大小的變換操作。這些操作也用於將世界座標系中的場景描述轉換為輸出裝置上顯示的觀察子程式中。另外，它們用於各種其他的應用中，如計算機輔助設計和計算機動畫。例如，一個建築設計師通過安排組成部分的方向和大小來建立一個設計佈局圖，而計算機動畫師通過沿指定路徑移動“照相機”位置或場景中的物件來開發一個視訊序列。應用於物件幾何描述並改變它的位置、方向或大小的操作稱為幾何變換(geometric transformation)。
幾何變換有時也稱為建模變換(modeling transformation )
4.1 基本的二維幾何變換
平移、旋轉和縮放是所有圖形軟體包中都含有的幾何變換函式。其他可能包括在圖形軟體包中的變換函式有反射和錯切操作。為了介紹幾何變換的一般概念，我們首先考慮二維操作，然後討論這些基本的思想怎樣擴充到三維場景中。在理解基本的概念後，我們可以很容易地編寫執行二維場景物件幾何變換的程式。
4.1.1 二維變換
通過將位移量加到一個點的座標上來生成一個新的座標位置，可以實現一次平移(translation)。實際上，我們將該點從原始位置沿一直線路徑移動到新位置。類似地，對於一個用多個座標位置定義的物件(如四邊形)，可以通過對所有座標位置使用相同的位移量沿平行路徑重定位來實現平移。然後在新位置顯示完整的物件。
將平移距離(translation distance ) tx和ty加到原始座標(x, y)上獲得一個新的座標位置(x', y')，可以實現一個二維位置的平移，如圖所示。
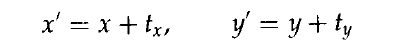一對平移距離(tx, ty)稱為平移向量(translation
vector)或位移向量( shift vector )。
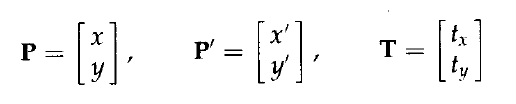
這樣就可以使用矩陣形式來表示二維平移方程：
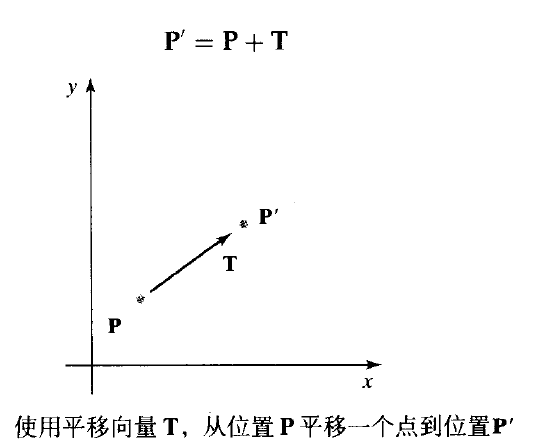
平移是一種移動物件而不改變其形狀的剛體變換。即物件上的每一點移動了同樣的距離。一條直線段的平移通過使用方程(5.3)對其兩端點進行移動並重畫兩個新端點位置間的線段來實現。多邊形也以類似的方法平移。我們將平移向量加到多邊形的每一頂點座標位置，然後使用這組新端點來重新生成多邊形。
下面的程式演示了平移操作。輸入的平移向量用來將一個多邊形的n個頂點從一個世界座標系移動到另一個，而OpenGL子程式用來重新生成平移後的多邊形。
如果要刪除原來的多邊形，則可以在平移前用背景色顯示它。有些圖形軟體包中有另外的刪除圖形部分的方法。同樣，如果要儲存原來的多邊形位置，可以將平移後的多邊形存入不同的陣列。
可以使用同樣的方法來平移其他物件。為了改變圓或橢圓的位置，可以平移中心座標並在新的中心位置上重畫圖形。對於一個樣條曲線，通過平移定義該曲線路徑的點，然後使用平移過的座標位置來重構曲線。
使用線段和填充區等圖元來描述場景，並利用屬性來輔助這些圖元。我們給出了掃描線演算法，可以將圖元顯示在光柵裝置上。現在，再看看可用於物件重定位或改變大小的變換操作。這些操作也用於將世界座標系中的場景描述轉換為輸出裝置上顯示的觀察子程式中。另外，它們用於各種其他的應用中，如計算機輔助設計和計算機動畫。例如，一個建築設計師通過安排組成部分的方向和大小來建立一個設計佈局圖，而計算機動畫師通過沿指定路徑移動“照相機”位置或場景中的物件來開發一個視訊序列。應用於物件幾何描述並改變它的位置、方向或大小的操作稱為幾何變換(geometric transformation)。
幾何變換有時也稱為建模變換(modeling transformation )
4.1 基本的二維幾何變換
平移、旋轉和縮放是所有圖形軟體包中都含有的幾何變換函式。其他可能包括在圖形軟體包中的變換函式有反射和錯切操作。為了介紹幾何變換的一般概念，我們首先考慮二維操作，然後討論這些基本的思想怎樣擴充到三維場景中。在理解基本的概念後，我們可以很容易地編寫執行二維場景物件幾何變換的程式。
4.1.1 二維變換
通過將位移量加到一個點的座標上來生成一個新的座標位置，可以實現一次平移(translation)。實際上，我們將該點從原始位置沿一直線路徑移動到新位置。類似地，對於一個用多個座標位置定義的物件(如四邊形)，可以通過對所有座標位置使用相同的位移量沿平行路徑重定位來實現平移。然後在新位置顯示完整的物件。
將平移距離(translation distance ) tx和ty加到原始座標(x, y)上獲得一個新的座標位置(x', y')，可以實現一個二維位置的平移，如圖所示。
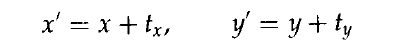一對平移距離(tx, ty)稱為平移向量(translation
vector)或位移向量( shift vector )。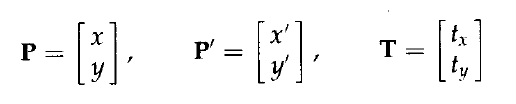
這樣就可以使用矩陣形式來表示二維平移方程：
平移是一種移動物件而不改變其形狀的剛體變換。即物件上的每一點移動了同樣的距離。一條直線段的平移通過使用方程(5.3)對其兩端點進行移動並重畫兩個新端點位置間的線段來實現。多邊形也以類似的方法平移。我們將平移向量加到多邊形的每一頂點座標位置，然後使用這組新端點來重新生成多邊形。
下面的程式演示了平移操作。輸入的平移向量用來將一個多邊形的n個頂點從一個世界座標系移動到另一個，而OpenGL子程式用來重新生成平移後的多邊形。
class wcPt2D {
public:
GLfloat x, y;
};
void translatePolygon (wcPt2D * verts, GLint nVerts, GLfloat tx, GLfloat ty)
{
GLint k;
for (k = 0; k < nVerts; k++){
verts [k].x = verts [k].x + tx;
verts [k].y = verts [k].y + ty;
}
glBegin (GL_POLYGON);
for (k = 0; k < nVerts; k++)
glVertex2f (verts [k].x, verts [k].y);
glEnd();
}如果要刪除原來的多邊形，則可以在平移前用背景色顯示它。有些圖形軟體包中有另外的刪除圖形部分的方法。同樣，如果要儲存原來的多邊形位置，可以將平移後的多邊形存入不同的陣列。
可以使用同樣的方法來平移其他物件。為了改變圓或橢圓的位置，可以平移中心座標並在新的中心位置上重畫圖形。對於一個樣條曲線，通過平移定義該曲線路徑的點，然後使用平移過的座標位置來重構曲線。