安卓圖形matrix矩陣變換的數學原理及程式碼
第一部分 Matrix的數學原理
在Android中,如果你用Matrix進行過影象處理,那麼一定知道Matrix這個類。Android中的Matrix是一個3 x 3的矩陣,其內容如下:
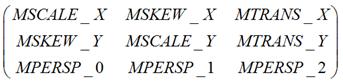
Matrix的對影象的處理可分為四類基本變換:
Translate 平移變換
Rotate 旋轉變換
Scale 縮放變換
Skew 錯切變換
從字面上理解,矩陣中的MSCALE用於處理縮放變換,MSKEW用於處理錯切變換,MTRANS用於處理平移變換,MPERSP用於處理透視變換。實際中當然不能完全按照字面上的說法去理解Matrix。同時,在Android的文件中,未見到用Matrix進行透視變換的相關說明,所以本文也不討論這方面的問題。
針對每種變換,Android提供了pre、set和post三種操作方式。其中
set用於設定Matrix中的值。
pre是先乘,因為矩陣的乘法不滿足交換律,因此先乘、後乘必須要嚴格區分。先乘相當於矩陣運算中的右乘。
post是後乘,因為矩陣的乘法不滿足交換律,因此先乘、後乘必須要嚴格區分。後乘相當於矩陣運算中的左乘。
除平移變換(Translate)外,旋轉變換(Rotate)、縮放變換(Scale)和錯切變換(Skew)都可以圍繞一箇中心點來進行,如果不指定,在預設情況下是圍繞(0, 0)來進行相應的變換的。
下面我們來看看四種變換的具體情形。由於所有的圖形都是有點組成,因此我們只需要考察一個點相關變換即可。
一、 平移變換
假定有一個點的座標是 ,將其移動到
,將其移動到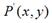 ,再假定在x軸和y軸方向移動的大小分別為:
,再假定在x軸和y軸方向移動的大小分別為:
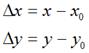
如下圖所示:
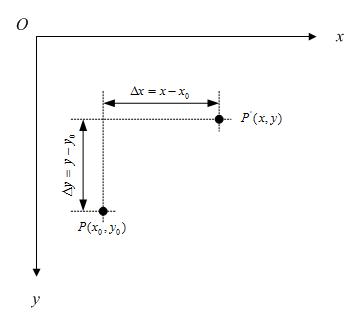
不難知道:
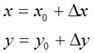
如果用矩陣來表示的話,就可以寫成:
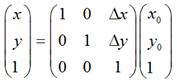
二、 旋轉變換
2.1 圍繞座標原點旋轉:
假定有一個點 ,相對座標原點順時針旋轉
,相對座標原點順時針旋轉 後的情形,同時假定P點離座標原點的距離為r,如下圖:
後的情形,同時假定P點離座標原點的距離為r,如下圖:
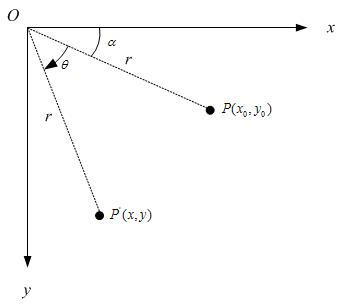
那麼,
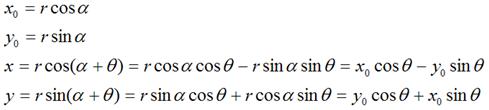
如果用矩陣,就可以表示為:
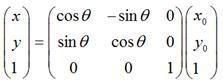
2.2 圍繞某個點旋轉
如果是圍繞某個點 順時針旋轉
順時針旋轉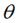 ,那麼可以用矩陣表示為:
,那麼可以用矩陣表示為:
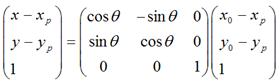
可以化為:
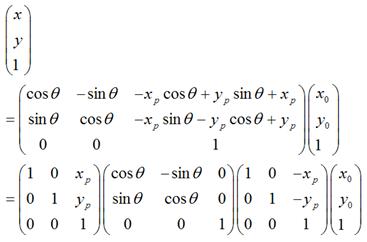
很顯然,
1.
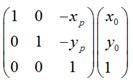 是將座標原點移動到點
是將座標原點移動到點 後,
後, 的新座標。
的新座標。
2.
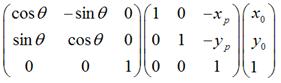
是將上一步變換後的 ,圍繞新的座標原點順時針旋轉
,圍繞新的座標原點順時針旋轉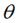 。
。
3.
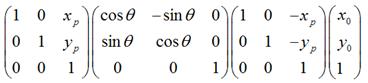
經過上一步旋轉變換後,再將座標原點移回到原來的座標原點。
所以,圍繞某一點進行旋轉變換,可以分成3個步驟,即首先將座標原點移至該點,然後圍繞新的座標原點進行旋轉變換,再然後將座標原點移回到原先的座標原點。
三、 縮放變換
理論上而言,一個點是不存在什麼縮放變換的,但考慮到所有影象都是由點組成,因此,如果影象在x軸和y軸方向分別放大k1和k2倍的話,那麼影象中的所有點的x座標和y座標均會分別放大k1和k2倍,即
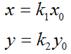
用矩陣表示就是:

縮放變換比較好理解,就不多說了。
四、 錯切變換
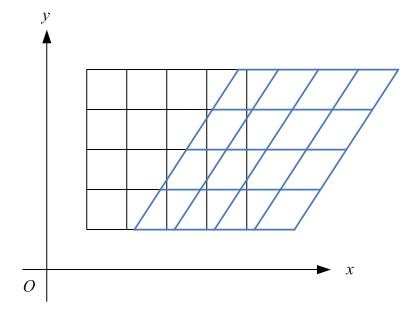
錯切變換(skew)在數學上又稱為Shear mapping(可譯為“剪下變換”)或者Transvection(縮並),它是一種比較特殊的線性變換。錯切變換的效果就是讓所有點的x座標(或者y座標)保持不變,而對應的y座標(或者x座標)則按比例發生平移,且平移的大小和該點到x軸(或y軸)的垂直距離成正比。錯切變換,屬於等面積變換,即一個形狀在錯切變換的前後,其面積是相等的。
比如下圖,各點的y座標保持不變,但其x座標則按比例發生了平移。這種情況將水平錯切。
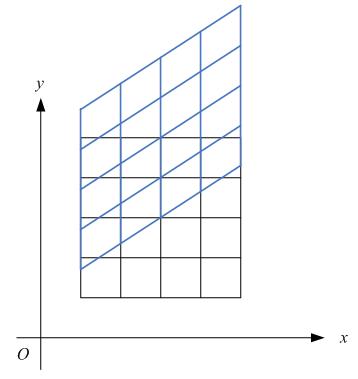
下圖各點的x座標保持不變,但其y座標則按比例發生了平移。這種情況叫垂直錯切。
假定一個點 經過錯切變換後得到
經過錯切變換後得到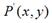 ,對於水平錯切而言,應該有如下關係:
,對於水平錯切而言,應該有如下關係:
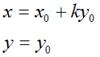
用矩陣表示就是:
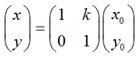
擴充套件到3 x 3的矩陣就是下面這樣的形式:
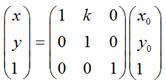
同理,對於垂直錯切,可以有:
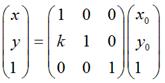
在數學上嚴格的錯切變換就是上面這樣的。在Android中除了有上面說到的情況外,還可以同時進行水平、垂直錯切,那麼形式上就是:

五、 對稱變換
除了上面講到的4中基本變換外,事實上,我們還可以利用Matrix,進行對稱變換。所謂對稱變換,就是經過變化後的影象和原影象是關於某個對稱軸是對稱的。比如,某點 經過對稱變換後得到
經過對稱變換後得到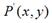 ,
,
如果對稱軸是x軸,難麼,
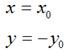
用矩陣表示就是:
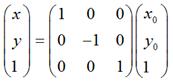
如果對稱軸是y軸,那麼,
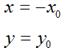
用矩陣表示就是:
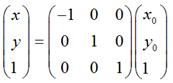
如果對稱軸是y = x,如圖:
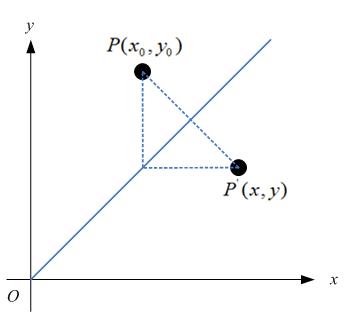
那麼,
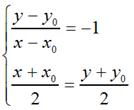
很容易可以解得:
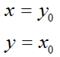
用矩陣表示就是:
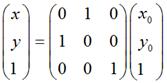
同樣的道理,如果對稱軸是y = -x,那麼用矩陣表示就是:
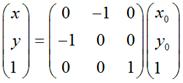
特殊地,如果對稱軸是y = kx,如下圖:
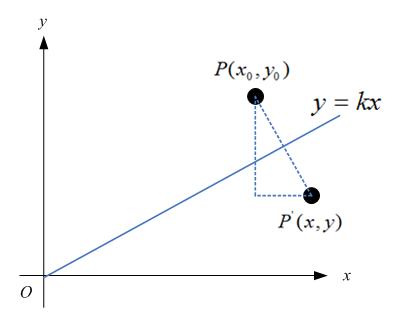
那麼,
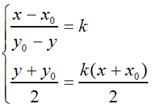
很容易可解得:
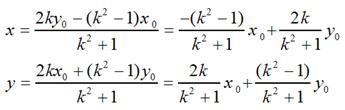
用矩陣表示就是:
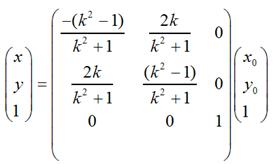
當k = 0時,即y = 0,也就是對稱軸為x軸的情況;當k趨於無窮大時,即x = 0,也就是對稱軸為y軸的情況;當k =1時,即y = x,也就是對稱軸為y = x的情況;當k = -1時,即y = -x,也就是對稱軸為y = -x的情況。不難驗證,這和我們前面說到的4中具體情況是相吻合的。
如果對稱軸是y = kx + b這樣的情況,只需要在上面的基礎上增加兩次平移變換即可,即先將座標原點移動到(0, b),然後做上面的關於y = kx的對稱變換,再然後將座標原點移回到原來的座標原點即可。用矩陣表示大致是這樣的:
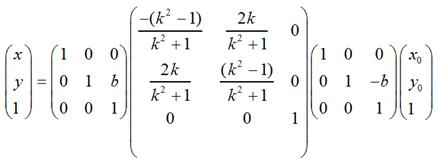
需要特別注意:在實際程式設計中,我們知道螢幕的y座標的正向和數學中y座標的正向剛好是相反的,所以在數學上y = x和螢幕上的y = -x才是真正的同一個東西,反之亦然。也就是說,如果要使圖片在螢幕上看起來像按照數學意義上y = x對稱,那麼需使用這種轉換:
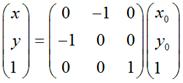
要使圖片在螢幕上看起來像按照數學意義上y = -x對稱,那麼需使用這種轉換:
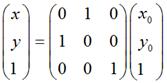
關於對稱軸為y = kx 或y = kx + b的情況,同樣需要考慮這方面的問題。
第二部分 程式碼驗證
在第一部分中講到的各種影象變換的驗證程式碼如下,一共列出了10種情況。如果要驗證其中的某一種情況,只需將相應的程式碼反註釋即可。試驗中用到的圖片:

其尺寸為162 x 251。
每種變換的結果,請見程式碼之後的說明。
Java程式碼- <span style="font-size:13px;"></span><pre name="code" class="java">package com.pat.testtransformmatrix;
- import android.app.Activity;
- import android.content.Context;
- import android.graphics.Bitmap;
- import android.graphics.BitmapFactory;
- import android.graphics.Canvas;
- import android.graphics.Matrix;
- import android.os.Bundle;
- import android.util.Log;
- import android.view.MotionEvent;
- import android.view.View;
- import android.view.Window;
- import android.view.WindowManager;
- import android.view.View.OnTouchListener;
- import android.widget.ImageView;
- public class TestTransformMatrixActivity extends Activity
- implements
- OnTouchListener
- {
- private TransformMatrixView view;
- @Override
- public void onCreate(Bundle savedInstanceState)
- {
- super.onCreate(savedInstanceState);
- requestWindowFeature(Window.FEATURE_NO_TITLE);
- this.getWindow().setFlags(WindowManager.LayoutParams.FLAG_FULLSCREEN, WindowManager.LayoutParams.FLAG_FULLSCREEN);
- view = new TransformMatrixView(this);
- view.setScaleType(ImageView.ScaleType.MATRIX);
- view.setOnTouchListener(this);
- setContentView(view);
- }
- class TransformMatrixView extends ImageView
- {
- private Bitmap bitmap;
- private Matrix matrix;
- public TransformMatrixView(Context context)
- {
- super(context);
- bitmap = BitmapFactory.decodeResource(getResources(), R.drawable.sophie);
- matrix = new Matrix();
- }
- @Override
- protected void onDraw(Canvas canvas)
- {
- // 畫出原影象
- canvas.drawBitmap(bitmap, 0, 0, null);
- // 畫出變換後的影象
- canvas.drawBitmap(bitmap, matrix, null);
- super.onDraw(canvas);
- }
- @Override
- public void setImageMatrix(Matrix matrix)
- {
- this.matrix.set(matrix);
- super.setImageMatrix(matrix);
- }
- public Bitmap getImageBitmap()
- {
- return bitmap;
- }
- }
- public boolean onTouch(View v, MotionEvent e)
- {
- if(e.getAction() == MotionEvent.ACTION_UP)
- {
- Matrix matrix = new Matrix();
- // 輸出影象的寬度和高度(162 x 251)
- Log.e("TestTransformMatrixActivity", "image size: width x height = " + view.getImageBitmap().getWidth() + " x " + view.getImageBitmap().getHeight());
- // 1. 平移
- matrix.postTranslate(view.getImageBitmap().getWidth(), view.getImageBitmap().getHeight());
- // 在x方向平移view.getImageBitmap().getWidth(),在y軸方向view.getImageBitmap().getHeight()
- view.setImageMatrix(matrix);
- // 下面的程式碼是為了檢視matrix中的元素
- float[] matrixValues = new float[9];
- matrix.getValues(matrixValues);
- for(int i = 0; i < 3; ++i)
- {
- String temp = new String();
- for(int j = 0; j < 3; ++j)
- {
- temp += matrixValues[3 * i + j ] + "\t";
- }
- Log.e("TestTransformMatrixActivity", temp);
- }
-
相關推薦
安卓圖形matrix矩陣變換的數學原理及程式碼
第一部分 Matrix的數學原理 在Android中,如果你用Matrix進行過影象處理,那麼一定知道Matrix這個類。Android中的Matrix是一個3 x 3的矩陣,其內容如下: Matrix的對影象的處理可分為四類基本變換: T
二維圖形的矩陣變換(一)——基本概念
tcl aid 縮放 clas 數學家 hang matrix log css3 原文:二維圖形的矩陣變換(一)——基本概念基本的二維變換可包括旋轉、縮放、扭曲,和平移四種, 而這些幾何運算則可以轉換為一些基本的矩陣運算:
二維圖形的矩陣變換(三)——在WPF中的應用矩陣變換
over 底層 hit 過程 相對 duration != closed com 原文:二維圖形的矩陣變換(三)——在WPF中的應用矩陣變換UIElement和RenderTransform 首先,我們來看看什麽樣的對象可以進行變換。在WPF中,用於呈現給用戶的對象的基
Android-Fk:[開源框架] 安卓崩潰資訊收集框架ACRA原理流程
Android-Fk:[開源框架] 安卓崩潰資訊收集框架ACRA原理流程 本文主要梳理ACRA原理及程式碼流程 順序圖的uml檔案 簡化圖的draw.io原始檔 分享至百度網盤 https://pan.baidu.com/s/1zAapEu9mmOZsTMDlCRCRQg 一. 學習
慕課網/安卓攻城獅視頻學習及練習(四)
cti row fcm dma term relative man water 形式 relativelayout 子類控件自身的位置屬性: framelayout absolutelayout很少使用 tablelayout 五布局
慕課網/安卓攻城獅視頻學習及練習(五)——簡陋計算器
!= activit 技術分享 lis 傳遞 ride iss alt result 簡陋計算器 1 public class FActivity extends Activity implements OnClickListener{ 2
慕課網/安卓攻城獅視頻學習及練習(六)
lba etl 居住 style 北京 click con notify absl manifest A跳轉B,在B的文件中用permission權限,然後A就無權跳轉到B,如果在A中用uses-permission把權限給了A,那麽A就可以跳轉到B了.可以通俗的說,
協方差、協方差矩陣的數學概念及演算法計算
在講解協方差之前,我們先一起回憶一下樣本的均值、方差、標準差的定義。 方差,協方差和協方差矩陣 1、概念 方差(Variance)是度量一組資料的分散程度。方差是各個樣本與樣本均值的差的平方和的均值: 協方差(Covariance)是度量兩個變數的變動的同步程度
安卓 視訊直播二:推流端程式碼
想要從底層一步步寫起比較麻煩,需要了解一點影象處理的知識,為了快速開發,我選擇通過第三方的SDK,這裡簡單說一下第三方SDK,其中有騰訊,阿里,百度雲,網易,金山雲,抖音,大牛都支援不過各有利弊。 (1)騰訊雲ILVB實名認證後需要人工稽核5個工作日,反正至今沒有看到SDK; (2)阿里
pytorch中的CrossEntropyLoss()函式——交叉熵的數學原理及應用
分類問題中,交叉熵函式是比較常用也是比較基礎的損失函式,原來就是了解,但一直搞不懂他是怎麼來的?為什麼交叉熵能夠表徵真實樣本標籤和預測概率之間的差值?趁著這次學習把這些概念系統學習了一下。 首先說起交叉熵,腦子裡就會出現這個東西: 隨後
安卓減小apk的體積,整體優化程式碼
百度到的方法都太普通,還是通過as自帶的功能來實現吧,有兩種方法。 1、首先生成apk檔案,點選Build->Build Apk(s),然後再點選Build->Analyze Apk...會生成如下介面。可以直觀的看出到底是那一部分佔的記憶體大。
基於安卓5.0水波紋效果製作及自定義水波紋顏色
安卓5.0以後很多ui效果的改進都是為提高使用者體驗,其中水波紋效果是5.0以後是在互動方式中做的特殊處理 接下來學習一下水波紋的簡單使用及水波紋顏色的自定義。 首先佈局檔案中給控制元件設定為可點
離散餘弦變換_原理及應用
1.預備知識 1.1可分離變換 二維傅立葉變換可用通用的關係式來表示: 式中:x, u=0, 1, 2, …, M-1;y, v=0, 1, 2, …, N-1;g(x,y,u,v
安卓中的訊息迴圈機制Handler及Looper詳解
我們知道安卓中的UI執行緒不是執行緒安全的,我們不能在UI執行緒中進行耗時操作,通常我們的做法是開啟一個子執行緒在子執行緒中處理耗時操作,但是安卓規定不允許在子執行緒中進行UI的更新操作,通常我們會通過Handler機制來完成該功能,即當子執行緒中耗時操作完成後,在子執行緒
安卓開發環境Android SDK下載安裝及配置教程
Android開發環境搭建分為以下四步:第一步、安裝JDK;第二步、安裝Eclipse;第三步、下載並安裝AndroidSDK;第四步、在Unity中釋出到Android平臺。安裝JDK官網:http://www.Oracle.com/technetwork/Java/jav
安卓5.0通知遇到的問題及原因
首先是傳送普通通知的一段程式碼。 public void send(String string) { NotificationCompat.Builder mBuilder = new NotificationCompat.Builder(this);
霍夫變換的原理 及 一種引數迭代的自適應尋找最佳霍夫直線的程式碼(在條碼識別中的應用)
霍夫變換(Hough Transform)是一種識別幾何形狀的方法!霍夫變換的基本原理是利用點與線的對偶性,將原始影象空間的給定的曲線通過曲線表達形式變為引數空間的一個點。這樣就把原始影
OpenCV(一)——高斯卷積核原理及程式碼實現
貼出getGaussianKernel原始碼 在smooth.cpp中 提示:Gaussian核基於 正態分佈函式設計 μ是均值,σ^2是方差 正態函式(即一維Gaussian卷積核)如下 二維卷積核通過對一維積分得到,並且μ = 0 根據如下原始碼可知
batchnorm原理及程式碼詳解(筆記2)
Batchnorm原理詳解 前言:Batchnorm是深度網路中經常用到的加速神經網路訓練,加速收斂速度及穩定性的演算法,可以說是目前深度網路必不可少的一部分。 本文旨在用通俗易懂的語言,對深度學習的常用演算法–batchnorm的原理及其程式碼實現做一個詳細的解讀。本文主要包括以下幾個
微信公眾號掃碼登陸原理及程式碼實現
1.使用者開啟公眾號點選掃碼功能(注意我們用 scancode_waitmsg這種型別即可) 2.使用者掃描了二維碼會給微信傳送資訊,然後微信把資訊以XML格式傳送給我們的伺服器 3.接收資料,並把資料保存於資料庫或者快取,程式碼如下: $wechatObj = new
