機器學習實戰專輯part2——K-近鄰法@[適合初學小白超詳細!]

前段時間忙小論文和專利，寫部落格耽擱了好久，終於終於有時間可以繼續寫了，雖然沒記錄在部落格上，但是學習依然沒有鬆懈，廢話不多說，今天歡迎我們的主角登場，K-近鄰法。

一、K-近鄰法基本概念

K-近鄰法也叫KNN是一種基本分類與迴歸方法，一般是用來解決分類問題，它的輸入為例項的特徵向量，對應於特徵空間的點，輸出為例項的類別，可以取多類。K-近鄰法假設給定一個訓練資料集，其中例項的類別已定，分類時，對新的例項，根據其K個最近鄰訓練例項的類別，通過多數表決的等方式進行預測。K-近鄰法沒有顯式的學習過程。
思路

K-近鄰是通過測量不同特徵值之間的距離進行分類。它的思路是：如果一個樣本在特徵空間中的k個最相似(即特徵空間中最鄰近)的樣本中的大多數屬於某一個類別，則該樣本也屬於這個類別，其中K通常是不大於20的整數。KNN演算法中，所選擇的鄰居都是已經正確分類的物件。該方法在定類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。
三個基本要素

1.K值的選擇
對於k值的選擇，沒有一個固定的經驗，一般根據樣本的分佈，選擇一個較小的值，可以通過交叉驗證選擇一個合適的k值。

選擇較小的k值，就相當於用較小的領域中的訓練例項進行預測，訓練誤差會減小，只有與輸入例項較近或相似的訓練例項才會對預測結果起作用，與此同時帶來的問題是泛化誤差會增大，換句話說，K值的減小就意味著整體模型變得複雜

，容易發生過擬合；

選擇較大的k值，就相當於用較大領域中的訓練例項進行預測，其優點是可以減少泛化誤差，但缺點是訓練誤差會增大。這時候，與輸入例項較遠（不相似的）訓練例項也會對預測器作用，使預測發生錯誤，且K值的增大就意味著整體的模型變得簡單。

一個極端是k等於樣本數m，則完全沒有分類，此時無論輸入例項是什麼，都只是簡單的預測它屬於在訓練例項中最多的類，模型過於簡單。

舉個栗子說明一下K值的選擇對分類結果的影響：
如下圖，綠色圓要被決定賦予哪個類，是紅色三角形還是藍色四方形？如果K=3，由於紅色三角形所佔比例為2/3，綠色圓將被賦予紅色三角形那個類，如果K=5，由於藍色四方形比例為3/5，因此綠色圓被賦予藍色四方形類。

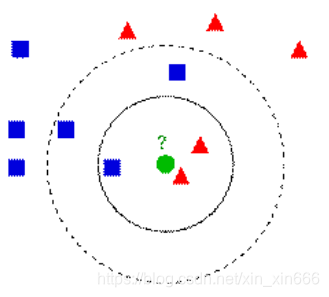
由此也說明了KNN演算法的結果很大程度取決於K的選擇。

2.距離度量
特徵空間中兩個例項點的距離是兩個例項點相似程度的反映，那麼如何度量這個距離呢？一般我們選擇歐式距離或更為一般的L_p距離。

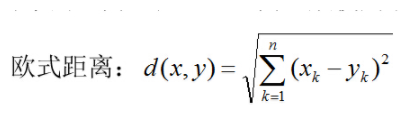
其中p=2,根據不同的p值選擇，也即不同的距離度量方法，確定的最近鄰點是不同的。

3.分類決策規則
k-近鄰法中的分類決策規則往往是多數表決，即由輸入例項的K個鄰近的訓練例項中的多數類決定輸入例項的類。多數表決規則等價於經驗風險最小化。

二、實現k-近鄰法虛擬碼

對未知類別屬性的資料集中的每個點依次執行以下操作：
（1）計算已知類別資料和當前點之間的距離
（2）按照距離遞增次序排序
（3）選取與當前距離最小的K個點
（4）確定前K個點所在類別的出現頻率
（5）返回前K個點出現頻率最高的類別作為當前點的預測分類

三、K近鄰法python程式碼實現

from numpy import *
import operator
 
def createDataSet():
	group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])  #我覺得可以這樣理解，每一種方括號都是一個維度（秩），這裡就是二維陣列，
                                                      #最裡面括著每一行的有一個方括號，後面又有一個，就是二維，四行
	labels=['A','A','B','B']
	return group,labels
 
def classify0(inX,dataSet,labels,k):             #inX是你要輸入的要分類的“座標”，dataSet是上面createDataSet的array，就是已經有的，
                                                #分類過的座標，label是相應分類的標籤，k是KNN，k近鄰里面的k
	dataSetSize=dataSet.shape[0]                     #dataSetSize是sataSet的行數，用上面的舉例就是4行
	diffMat=tile(inX,(dataSetSize,1))-dataSet         #前面用tile，把一行inX變成4行一模一樣的（tile有重複的功能，dataSetSize是重複4遍，
                                                    # 後面的1保證重複完了是4行，而不是一行裡有四個一樣的），然後再減去dataSet，
                                                   #是為了求兩點的距離，先要座標相減，這個就是座標相減
	sqDiffMat=diffMat**2                              #上一行得到了座標相減，然後這裡要(x1-x2)^2，要求乘方
	sqDistances=sqDiffMat.sum(axis=1)                 #axis=1是列相加，，這樣得到了(x1-x2)^2+(y1-y2)^2
	distances=sqDistances**0.5                        #開根號，這個之後才是距離
	sortedDistIndicies=distances.argsort()            #argsort是排序，將元素按照由小到大的順序返回下標，比如([3,1,2]),它返回的就是([1,2,3])
	classCount={}
	for i in range(k):
		voteIlabel=labels[sortedDistIndicies[i]]
		classCount[voteIlabel]=classCount.get(voteIlabel,0)+1 #get是取字典裡的元素，如果之前這個voteIlabel是有的，
                                                              #那麼就返回字典裡這個voteIlabel裡的值，如果沒有就返回0（後面寫的），
                                                              #這行程式碼的意思就是算離目標點距離最近的k個點的類別，
                                                              #這個點是哪個類別哪個類別就加1
	soredClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)         
    #key=operator.itemgetter(1)的意思是按照字典裡的第一個排序，{A:1,B:2},要按照第1個（AB是第0個），即‘1’‘2’排序。reverse=True是降序排序
	return soredClassCount[0][0]             #返回類別最多的類別

輸入以下語句進行測試：

group,labels=createDataSet()
classify0([0,0],group,labels,3)

返回B即為正確結果。

四、實戰

1.使用K-近鄰演算法改進約會網站的配對效果

from numpy import *
import operator
from collections import Counter
import matplotlib
import matplotlib.pyplot as plt


###匯入特徵資料
def file2matrix(filename):
    fr = open(filename)
    contain = fr.readlines()###讀取檔案的所有內容
    count = len(contain)
    returnMat = zeros((count,3))
    classLabelVector = []
    index = 0
    for line in contain:
        line = line.strip() ###擷取所有的回車字元
        listFromLine = line.split('\t')
        returnMat[index,:] = listFromLine[0:3]###選取前三個元素，儲存在特徵矩陣中
        classLabelVector.append(listFromLine[-1])###將列表的最後一列儲存到向量classLabelVector中
        index += 1
    
    ##將列表的最後一列由字串轉化為數字，便於以後的計算
    dictClassLabel = Counter(classLabelVector)
    classLabel = []
    kind = list(dictClassLabel)
    for item in classLabelVector:
        if item == kind[0]:
            item = 1
        elif item == kind[1]:
            item = 2
        else:
            item = 3
        classLabel.append(item)
    return returnMat,classLabel#####將文字中的資料匯入到列表

##繪圖（可以直觀的表示出各特徵對分類結果的影響程度）
datingDataMat,datingLabels = file2matrix('E:\datingTestSet.txt')
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDataMat[:,0],datingDataMat[:,1],15.0*array(datingLabels),15.0*array(datingLabels))
plt.show()

## 歸一化資料,保證特徵等權重
def autoNorm(dataSet):
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = zeros(shape(dataSet))##建立與dataSet結構一樣的矩陣
    m = dataSet.shape[0]
    for i in range(1,m):
        normDataSet[i,:] = (dataSet[i,:] - minVals) / ranges
    return normDataSet,ranges,minVals

##KNN演算法
def classify(input,dataSet,label,k):
    dataSize = dataSet.shape[0]
    ####計算歐式距離
    diff = tile(input,(dataSize,1)) - dataSet
    sqdiff = diff ** 2
    squareDist = sum(sqdiff,axis = 1)###行向量分別相加，從而得到新的一個行向量
    dist = squareDist ** 0.5
    
    ##對距離進行排序
    sortedDistIndex = argsort(dist)##argsort()根據元素的值從大到小對元素進行排序，返回下標

    classCount={}
    for i in range(k):
        voteLabel = label[sortedDistIndex[i]]
        ###對選取的K個樣本所屬的類別個數進行統計
        classCount[voteLabel] = classCount.get(voteLabel,0) + 1
    ###選取出現的類別次數最多的類別
    maxCount = 0
    for key,value in classCount.items():
        if value > maxCount:
            maxCount = value
            classes = key
    return classes

##測試(選取10%測試）
def datingTest():
    rate = 0.10
    datingDataMat,datingLabels = file2matrix('E:\datingTestSet.txt')
    normMat,ranges,minVals = autoNorm(datingDataMat)
    m = normMat.shape[0]
    testNum = int(m * rate)
    errorCount = 0.0
    for i in range(1,testNum):
        classifyResult = classify(normMat[i,:],normMat[testNum:m,:],datingLabels[testNum:m],3)
        print("分類後的結果為:,", classifyResult)
        print("原結果為：",datingLabels[i])
        if(classifyResult != datingLabels[i]):
                                  errorCount += 1.0
    print("誤分率為:",(errorCount/float(testNum)))
                                  
###預測函式
def classifyPerson():
    resultList = ['一點也不喜歡','有一丟丟喜歡','灰常喜歡']
    percentTats = float(input("玩視訊所佔的時間比?"))
    miles = float(input("每年獲得的飛行常客里程數?"))
    iceCream = float(input("每週所消費的冰淇淋公升數?"))
    datingDataMat,datingLabels = file2matrix('E:\datingTestSet2.txt')
    normMat,ranges,minVals = autoNorm(datingDataMat)
    inArr = array([miles,percentTats,iceCream])
    classifierResult = classify((inArr-minVals)/ranges,normMat,datingLabels,3)
    print("你對這個人的喜歡程度:",resultList[classifierResult - 1])

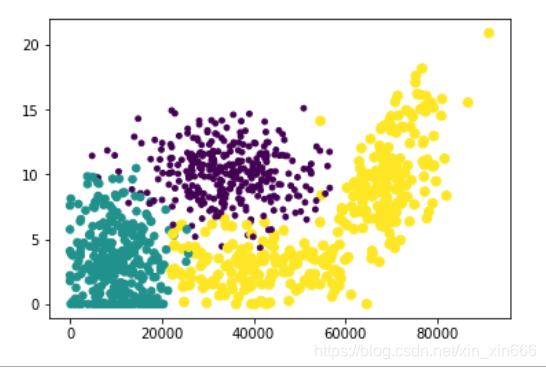
圖中，紫色部分為極具魅力，綠色部分為魅力一般，黃色部分為不喜歡
橫軸表示每年獲取的飛行常客里程數
縱軸表示玩視訊遊戲所耗時間百分比

五、KD樹

kd樹是為了降低KNN的時間複雜度，提升其效能的一種資料結構,是一種二叉樹，表示對K維空間的一個劃分。 使用 kd樹，可以對n維空間中的樣本點進行儲存以便對其進行快速搜尋。構造kd樹，相當於不斷地用垂直於座標軸的超平面將n維空間進行切分，構成一系列的n維超矩形區域。kd樹的每一個節點對應於一個n維超矩形區域。

構造KD樹演算法
輸入：K維空間資料集T
輸出：KD樹

1. 開始：構造根節點，根節點對應於包含T的k維空間的超矩形區域
   選擇x為座標軸，以T中所有例項的x座標的中位數為切分點，將根節點對應的矩 形區域切分為兩個子區域。切分由通過切分點並與座標軸x垂直的超平面實現。
   落在此切分超平面上的例項點就是根節點，左子節點對應著座標小於切分點的子區域，右子節點對應著座標大於切分點的子區域。

2. 重複：還是以該區域所有例項座標的中位數為切分點，重複步驟1.

3. 直到兩個子區域沒有例項存在時停止，從而形成KD樹劃分。

虛擬碼

演算法：構建k-d樹（createKDTree）  
    輸入：資料點集Data-set和其所在的空間Range  
    輸出：Kd，型別為k-d tree  
    1.If Data-set為空，則返回空的k-d tree  
    2.呼叫節點生成程式：  
    　　（1）確定split域：對於所有描述子資料（特徵向量），統計它們在每個維上的資料方差。假設每條資料記錄為64維，可計算64個方差。挑選出最大值，對應的維就是split域的值。資料方差大表明沿該座標軸方向上的資料分散得比較開，在這個方向上進行資料分割有較好的解析度；  
    　　（2）確定Node-data域：資料點集Data-set按其第split域的值排序。位於正中間的那個資料點被選為Node-data。此時新的Data-set' = Data-set \ Node-data（除去其中Node-data這一點）。  
    3.dataleft = {d屬於Data-set' && d[split] ≤ Node-data[split]}  
       Left_Range = {Range && dataleft}  
      dataright = {d屬於Data-set' && d[split] > Node-data[split]}  
       Right_Range = {Range && dataright}  
    4.left = 由（dataleft，Left_Range）建立的k-d tree，即遞迴呼叫createKDTree（dataleft，Left_Range）。並設定left的parent域為Kd；  
       right = 由（dataright，Right_Range）建立的k-d tree，即呼叫createKDTree（dataleft，Left_Range）。並設定right的parent域為Kd。  

具體步驟：
① 待分類樣本test_point，初始化best_dist為無窮大；
② 首先從根節點開始搜尋，確定當前節點弄得，計算當前節點與test_point之間的距離；
③ 若當前節點與test_point之間的距離小於best_dist，則將當前節點與test_point之間的距離賦值給best_dist；
④ 確定當前節點的劃分維度，即split；
⑤ 利用當前結點的劃分閾值node.node_data[node.split]來向下搜尋，若測試樣本當前維的值test_point[split]小於當前節點閾值，則搜尋左子樹，否則，搜尋右子樹。
⑥ 採用遞迴的方式繼續對左子樹（或右子樹）進行搜尋，獲得best_dist;
⑦ 至此，我們僅搜尋了左子樹（或右子樹），另外一個子樹是否要進行搜尋呢？答案是需要的，因為我們並不能確定那邊沒有距離更近的樣本點。
⑧ 那這樣不是和暴力搜尋沒有差別了？當然不是！
⑨ 假設測試樣本當前維值為test_point[split]=4， 當前結點當前維的值為node.node_data[node.split]=15，所以，我們搜尋的是左子樹，假設我們搜尋完左子樹得到的最短距離為best_dist=3， 那我們可以計算當前結點與測試樣本在當前維的距離err_dist=node.node_data[split] - test_point[split]， 若其大於best_dist，則不需要搜尋右子樹了，因為根據kd樹的結構，右子樹所有結點在當前維axis的值肯定大於10，則其與測試樣本的距離肯定大於best_dist（因為test_point[split]是小於10的，且某一維度的差值大於best_dist，則其常用距離，不論是歐式或馬氏距離，肯定是大於best_dist）。這樣我們就可以捨棄一部分割槽域，從而縮小了搜尋空間。

上述方法，將最近鄰搜尋的時間複雜度從暴力搜尋的O(n)降低至O(log(n))基於kd樹的最 近鄰搜尋 K近鄰的搜尋，其實是通過上述方法，構建長度為K的有界優先佇列，儲存和不斷的更新當前搜尋過程中與待分類樣本點距離最近的K個樣本點的即距離。

六、總結

1.KNN演算法優缺點
優點：
① 簡單，易於理解，易於實現，無需引數估計，無需訓練;
② 對異常值不敏感（個別噪音資料對結果的影響不是很大）;
③ 適合對稀有事件進行分類;
④ 適合於多分類問題(multi-modal,物件具有多個類別標籤)，KNN要比SVM表現要好;
缺點：
① 對測試樣本分類時的計算量大，記憶體開銷大，因為對每一個待分類的文字都要計算它到全體已知樣本的距離，才能求得它的K個最近鄰點。目前常用的解決方法是事先對已知樣本點進行剪輯，事先去除對分類作用不大的樣本;
② 可解釋性差，無法告訴你哪個變數更重要，無法給出決策樹那樣的規則;
③ K值的選擇：最大的缺點是當樣本不平衡時，如一個類的樣本容量很大，而其他類樣本容量很小時，有可能導致當輸入一個新樣本時，該樣本的K個鄰居中大容量類的樣本佔多數。該演算法只計算“最近的”鄰居樣本，某一類的樣本數量很大，那麼或者這類樣本並不接近目標樣本，或者這類樣本很靠近目標樣本。無論怎樣，數量並不能影響執行結果。可以採用權值的方法（和該樣本距離小的鄰居權值大）來改進;
④ KNN是一種消極學習方法、懶惰演算法。

2.KNN效能問題
KNN的效能問題也是KNN的缺點之一。使用KNN，可以很容易的構造模型，但在對待分類樣本進行分類時，為了獲得K近鄰，必須採用暴力搜尋的方式，掃描全部訓練樣本並計算其與待分類樣本之間的距離，系統開銷很大。

作者：小新新
來源：CSDN
版權宣告：本文為博主原創文章，轉載請附上博文連結！歡迎轉載！

---

參考文獻：

[1]《機器學習實戰》的第二章內容
[2] 《統計學習方法（李航）》