本文 參考自李航博士的《統計學習方法》 為自我理解的簡化版本

3.1 K近鄰演算法

給定一個訓練資料集，對新的輸入例項，在訓練資料集中找到與該例項最鄰近的k個例項，這k個例項的多數屬於某個類，就把該輸入例項分為這個類。

I為指示函式，即當 yi=ci$y_i=c_i$ 時 I$I$ 為1，否則 I$I$ 為 0。

3.2 K近鄰模型

3.2.1 距離度量

特徵空間中兩個例項點的距離是兩個例項點相似程度的反映。使用的距離一般是歐式距離，也可以是 Lp$L_p$ 距離 或 M

3.2.2 K值的選擇

在應用中，k值一般取一個比較小的數值。通常採用交叉驗證法來選取最優的k值。

3.2.3 分類決策規則

k近鄰法中的分類決策規則往往是多數表決，誤分類概率

對給定的例項 x∈X$x\in \mathcal{X}$,其最近鄰的k個訓練例項點構成的集合 Nk(x)$N_k(x)$ .如果涵蓋 Nk(x)$N_k(x)$ 的區域的類別為 cj$c_j$，那麼誤分類率

要使誤分類率最小即經驗風險最小，就要使 ∑xi∈NK(x)I(yi=ci)$\sum _{x_i\in N_K(x)}I(y_i=c_i)$ 最大，所以多數表決規則等價於經驗風險最小化。

3.3 K近鄰法的實現：kd樹

為什麼要使引入kd樹：

k近鄰法最簡單的實現就是線性掃描計算輸入例項點與每個訓練例項的距離，訓練集很大時，這種方法是不可取的。
為了提高k近鄰搜尋的效率，可以使用像kd樹這樣的特殊結構儲存訓練資料，以減少計算距離的次數。

3.2.1 kd樹 ：構造

演算法：構造kd樹（createKDTree）

來自百度

輸入：k$k$ 維空間資料集 Data$Data$ set$set$ 和其所在的空間 Range$Range$
輸出：kd$kd$ tree$tree$

1. 如果資料集 Data$Data$ set$set$ 為空，則返回空的 kd$kd$ tree$tree$

2. 呼叫節點生成程式：
   （1）確定split域：對於所有描述子資料（特徵向量），統計它們在每個維上的資料方差。
   以SURF特徵為例，描述子為64維，可計算64個方差。
   挑選出最大值，對應的維就是split域的值。
   資料方差大表明沿該座標軸方向上的資料分散得比較開，在這個方向上進行資料分割有較好的解析度；
   （2）確定Node-data域：
   資料點集Data-set按其第split域的值排序。
   位於正中間(中位數)的那個資料點被選為Node-data。
   此時新的Data-set’ = Data-set \ Node-data（除去其中Node-data這一點）。

3. dataleft = { d屬於 Data-set’ && d [split] ≤ Node - data [split] }
   Left_Range = { Range && dataleft }
   dataright = { d屬於 Data-set’ && d [split] > Node - data [split] }
   Right_Range = { Range && dataright }

4. left = 由（dataleft，Left_Range）建立的k-d tree，
   即遞迴呼叫createKDTree（dataleft，Left_Range），並設定left的parent域為Kd；
   right = 由（dataright，Right_Range）建立的k-d tree，
   即呼叫createKDTree（dataright，Right_Range），並設定right的parent域為Kd。

舉個栗子

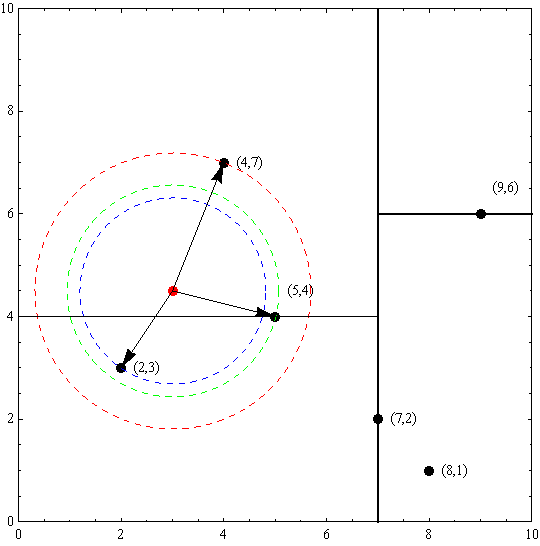
假設有6個二維資料點{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，資料點位於二維空間內（如圖1中黑點所示）。

由於此例簡單，資料維度只有2維，所以可以簡單地給x，y兩個方向軸編號為0,1，也即split={0,1}。
（1）確定split域的首先該取的值。分別計算x，y方向上資料的方差得知x方向上的方差最大，所以split域值首先取0，也就是x軸方向；
（2）確定Node-data的域值。根據x軸方向的值2,5,9,4,8,7排序選出中值為7，所以Node-data = （7,2）。這樣，該節點的分割超平面就是通過（7,2）並垂直於split = 0（x軸）的直線x = 7；
（3）確定左子空間和右子空間。分割超平面x = 7將整個空間分為兩部分，如圖2所示。x < = 7的部分為左子空間，包含3個節點{（2,3），（5,4），（4,7）}；另一部分為右子空間，包含2個節點{（9,6），（8,1）}。

如演算法所述，k-d樹的構建是一個遞迴的過程。然後對左子空間和右子空間內的資料重複根節點的過程就可以得到下一級子節點（5,4）和（9,6）（也就是左右子空間的’根’節點），同時將空間和資料集進一步細分。如此反覆直到空間中只包含一個數據點，如圖1所示。最後生成的k-d樹如圖3所示。

3.2.1 kd樹 ：搜尋

演算法：kd 樹最近鄰搜尋

來自李航博士的《統計學習方法》

輸入： 已構造的kd樹；目標點；
輸出：x$x$ 的最近鄰。

（1） 在kd樹中找出包含目標點的葉結點：從根結點出發，遞迴的向下訪問kd樹。
若目標點當前維的座標值小於切分點的座標值，則移動到左子結點，否則移動到右子結點。直到子結點為葉結點為止；

(相當於二分查詢)

（2） 以此葉結點為“當前最近點”；

（3） 遞迴的向上回退，在每個結點進行以下操作：

　　（a） 如果該結點儲存的例項點比當前最近點距目標點更近，則以該例項點為“當前最近點”；

　　（b） 當前最近點一定存在於該結點一個子結點對應的區域。檢查該子結點的父結點的另一個子結點對應的區域是否有更近的點。具體的，檢查另一個子結點對應的區域是否與以目標點為球心、以目標點與“當前最近點”間的距離為半徑的超球體相交。如果相交，可能在另一個子結點對應的區域記憶體在距離目標更近的點，移動到另一個子結點。接著，遞迴的進行最近鄰搜尋。如果不相交，向上回退。

（4） 當回退到根結點時，搜尋結束。最後的“當前最近點”即為的最近鄰點。

舉個栗子

以先前構建好的kd樹為例，查詢目標點（3,4.5）的最近鄰點。同樣先進行二叉查詢，先從（7,2）查詢到（5,4）節點，在進行查詢時是由y = 4為分割超平面的，由於查詢點為y值為4.5，因此進入右子空間查詢到（4,7），形成搜尋路徑：（7,2）→（5,4）→（4,7），取（4,7）為當前最近鄰點。以目標查詢點為圓心，目標查詢點到當前最近點的距離2.69為半徑確定一個紅色的圓。然後回溯到（5,4），計算其與查詢點之間的距離為2.06，則該結點比當前最近點距目標點更近，以(5,4)為當前最近點。用同樣的方法再次確定一個綠色的圓，可見該圓和y = 4超平面相交，所以需要進入（5,4）結點的另一個子空間進行查詢。（2,3）結點與目標點距離為1.8，比當前最近點要更近，所以最近鄰點更新為（2，3），最近距離更新為1.8，同樣可以確定一個藍色的圓。接著根據規則回退到根結點(7,2)，藍色圓與x=7的超平面不相交，因此不用進入（7,2）的右子空間進行查詢。至此，搜尋路徑回溯完，返回最近鄰點（2,3），最近距離1.8。

參考來源：http://blog.csdn.net/u012422446/article/details/56486342