文章目錄

• 一、定義符號
• 二、中心化和標準化
• 三、Z-score 標準化
• 四、PCA 演算法的基本思想
• 五、求解 μ 與降維
• 六、參考

一、定義符號

主成分分析（Principal Components Analysis, PCA）是一種降維方法。為了更好的解釋該演算法，首先假設資料集為 $\{x^{}$

二、中心化和標準化

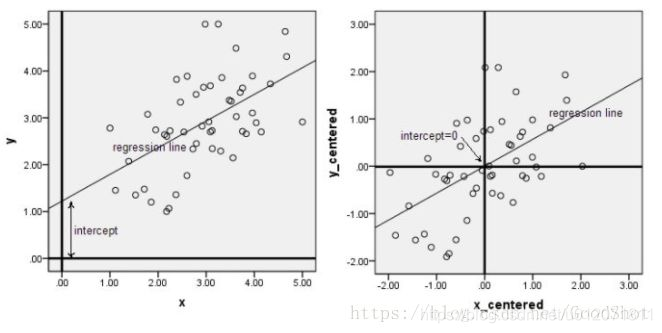
中心化又叫零均值化，中心化（零均值化）後的資料均值為零。下面兩幅圖是資料做中心化前後的對比，可以看到其實就是一個平移的過程，平移後所有資料的中心是(0, 0)。

資料標準化的目的就是使各個特徵都在同一尺度下被衡量。

三、Z-score 標準化

Z-score 標準化（也叫 0-1 標準化），這種方法給予原始資料的均值（mean）和標準差（standard deviation）進行資料的標準化。經過處理的資料符合標準正態分佈，即均值為 0，標準差為 1。Z-score 標準化的公式如下：

$x^{*} = \frac{x - \mu}{\sigma}$

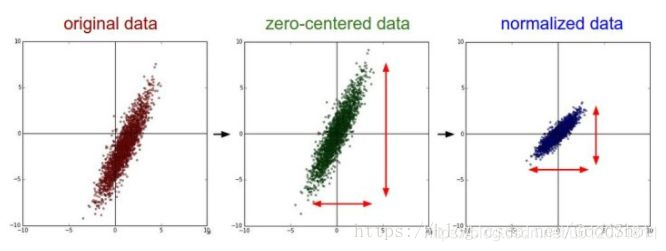
我們可以發現 Z-score 標準化的過程中是包含中心化的。以下圖片展示了一組資料進行 Z-score 標準化的過程。左圖表示的是原始資料，中間的是中心化後的資料，右圖是將中心化後的資料除以標準差，得到的標準化後的資料，可以看出每個維度上的尺度是一致的（紅色線段的長度表示尺度）。

想要使用 PCA 演算法，需要先對資料做以下處理：

1. $\mu = \frac{1}{m} \sum_{i=1}^{m} x^{(i)}$
2. $x^{(i)} = x^{(i)} - \mu$
3. $\sigma_j^2 = \frac{1}{m} \sum_i(x_j^{(i)})^2$
4. $x_j^{(i)} = \frac{x_j^{(i)}}{\sigma_j}$

整個過程其實就是 Z-score 標準化的過程。

四、PCA 演算法的基本思想

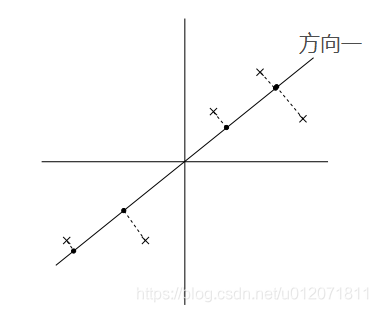
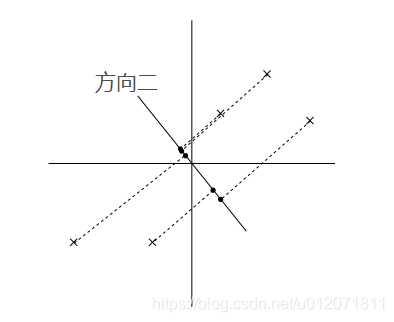
PCA 演算法的基本思想就是尋找到資料的主軸方向，我們希望資料在主軸方向上能夠被更好的區分開，直觀的說就是我們希望資料在主軸上儘量分散，更具體的就是指所有的點在主軸方向的投影點的方差最大。比如在以下兩個圖中，在方向一上，資料更分散，投影點的方差最大，所以如果從這兩個方向上選一個主軸的話，應該選方向一。

在資料已經做了 Z-score 標準化的前提下，資料的均值為 0，其投影點的均值也為 0。

$max \frac{1}{m} \sum_{i=1}^{m}(x^{(i)^T}u - 0)^2 \\ \Rightarrow max \frac{1}{m} \sum_{i=1}^{m} \mu^T x^{(i)} x^{(i)^T} \mu \\ \Rightarrow max \mu^T \Big( \frac{1}{m} \sum_{i=1}^m x^{(i)} x^{(i)^T} \Big) \mu \\$

(1) 上述第一個式子裡的 $x^{(i)^T} \mu$ 就是 $x^{(i)}$ 這個向量在投影方向 $\mu$ 上的長度。這裡的 $\mu$ 是單位向量，即 $\lVert \mu \rVert = 1$。
(2) 上述第二個式子是把向量內積的平方換了一個寫法。
(3) 上述第三個式子又對式子做了一個變形，不難看出 $ \frac{1}{m} \sum_{i=1}^m x^{(i)} x^{(i)T} $ 是一個矩陣，並且這個矩陣是對稱矩陣（實際上是一個協方差矩陣）。
(4) 縱觀整個式子，最終的目標則是找到使整個式子取到最大值的向量 $\mu$ ，所以這是一個最優化問題。

五、求解 μ 與降維

$\mu$ 是一個單位向量，這其實是這個最優化問題的約束條件（ $\lVert \mu \rVert = 1$），可以使用拉格朗日方程來求解該最優化問題：
$\begin{aligned} l =& \mu^T \Big( \frac{1}{m} \sum_{i=1}^m x^{(i)} x^{(i)^T} \Big) \mu - \lambda (\lVert \mu \rVert - 1)\\ =& \mu^T \Sigma \mu - \lambda(\mu^T \mu - 1) \end{aligned}$