『 特徵降維』PCA原理-Principal Component Analysis
特徵降維一般有兩類方法:特徵選擇和特徵抽取。特徵選擇即從高緯度的特徵中選擇其中的一個子集來作為新的特徵;而特徵抽取是指將高緯度的特徵經過某個函式對映至低緯度作為新的特徵。常用的特徵抽取方法就是PCA。
PCA(Principal Component Analysis)是一種常用的資料分析方法。PCA通過線性變換將原始資料進行線性變換、對映到低維空間中,使得各維度線性無關的表示,可用於提取資料的主要特徵分量。
向量的表示及基變換
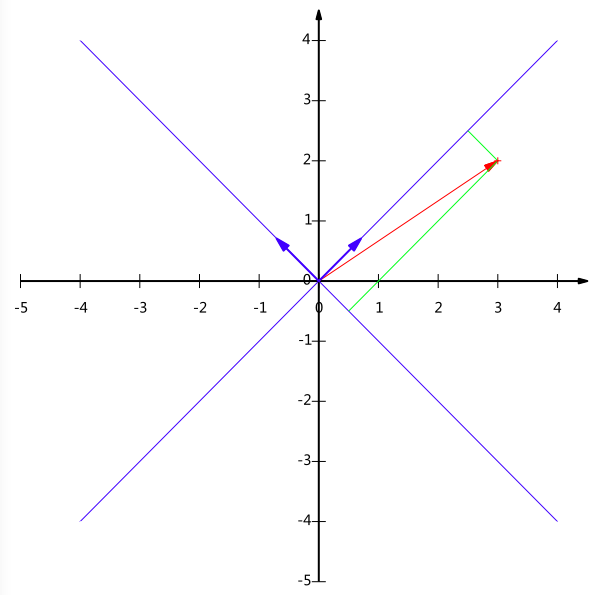
向量即為有方向和大小的量,例如a(3,2)本身可以表示向量,其中包含了隱式的定義:以x軸和y軸上正方向長度為1的向量為標準,
要準確描述向量,首先要確定一組基,然後給出在基所在的各個直線上的投影值,就可以了
一組基的唯一要求就是線性無關,非正交的基也是可以的。
基變換的矩陣表示
可以用矩陣的變換表示上面變數將基變為
變換的基向量,原始向量如圖:
有M個N維向量,想將其變換為由R個N維向量表示的新空間中,那麼首先將R個基按行組成矩陣A,然後將向量按列組成矩陣B,那麼兩矩陣的乘積AB就是變換結果,其中AB的第m列為A中第m列變換後的結果
其中
兩個矩陣相乘的意義是將右邊矩陣中的每一列列向量變換到左邊矩陣中每一行行向量為基所表示的空間中去
協方差矩陣及優化目標
如何選擇基才是最優的。或者說,如果我們有一組N維向量,現在要將其降到K維(K小於N),那麼我們應該如何選擇K個基才能最大程度保留原有的資訊?
如果我們必須使用低維來表示高緯資料,又希望儘量保留原始的資訊,要如何選擇?
通過上一節對基變換的討論我們知道,這個問題實際上是要在二維平面中選擇一個方向,將所有資料都投影到這個方向所在直線上,用投影值表示原始記錄。這是一個實際的二維降到一維的問題。
那麼如何選擇這個方向(或者說基)才能儘量保留最多的原始資訊呢?一種直觀的看法是:希望投影后的投影值儘可能分散。
方差
投影后投影值儘可能分散,而這種分散程度,可以用數學上的方差來表述。
其中,
尋找一個一維基,使得所有資料變換為這個基上的座標表示後,方差值最大。
協方差
找到一個方向使得投影后方差最大,這樣就完成了第一個方向的選擇,繼而我們選擇第二個投影方向。
單純只選擇方差最大的方向,很明顯,這個方向與第一個方向應該是“幾乎重合在一起”,因此不希望它們之間存在(線性)相關性的,因為相關性意味著兩個欄位不是完全獨立,必然存在重複表示的資訊。
數學上可以用兩個欄位的協方差表示其相關性,由於已經讓每個欄位均值為0,則:
相關推薦
『 特徵降維』PCA原理-Principal Component Analysis
特徵降維一般有兩類方法:特徵選擇和特徵抽取。特徵選擇即從高緯度的特徵中選擇其中的一個子集來作為新的特徵;而特徵抽取是指將高緯度的特徵經過某個函式對映至低緯度作為新的特徵。常用的特徵抽取方法就是PCA。 PCA(Principal Component An
基於OpenCV3實現人臉識別(原理篇)---PCA(Principal Component Analysis)
實踐總結: 1首先了解做人臉識別的步驟 2各個演算法後面的原理 3原理背後的相關知識的瞭解 4人臉識別專案總遇到的問題
從矩陣(matrix)角度討論PCA(Principal Component Analysis 主成分分析)、SVD(Singular Value Decomposition 奇異值分解)相關原理
0. 引言 本文主要的目的在於討論PAC降維和SVD特徵提取原理,圍繞這一主題,在文章的開頭從涉及的相關矩陣原理切入,逐步深入討論,希望能夠學習這一領域問題的讀者朋友有幫助。 這裡推薦Mit的Gilbert Strang教授的線性代數課程,講的非常好,循循善誘,深入淺出。 Relevant Link:&
主成分分析(PCA,Principal Component Analysis)
主成分分析(PCA,Principal Component Analysis) 1、理論 1)概要 &nbs
[機器學習]PCA(principal component analysis)
PCA(主成分分析)屬於無監督學習的範疇,是一種降維方法。PCA選取包含資訊量最多的方向對資料進行投影。1. 推導PCA的2種方法(需回顧)1)從重建誤差最小化的角度2)從方差最大化的角度(詳細推導見機器學習聖經 PRML )。2. 求解方法求解特徵值和特徵向量的方法分為 一
deep learning PCA(主成分分析)、主份重構、特徵降維
前言 前面幾節講到了深度學習採用的資料庫大小為28×28的手寫字,這對於機器學習領域算是比較低維的資料,一般圖片是遠遠大於這個尺寸的,比如256×256的圖片。然而特徵向量的維數過高會增加計算的複雜度,像前面訓練60000個28×28的手寫字,在我這個4G記憶體,C
【火爐煉AI】機器學習053-資料降維絕招-PCA和核PCA
【火爐煉AI】機器學習053-資料降維絕招-PCA和核PCA (本文所使用的Python庫和版本號: Python 3.6, Numpy 1.14, scikit-learn 0.19, matplotlib 2.2 ) 主成分分析(Principal Component Analysis, PCA)可以
機器學習實踐(五)—sklearn之特徵降維
一、特徵降維概述 為什麼要對特徵進行降維處理 如果特徵本身存在問題或者特徵之間相關性較強,對於演算法學習預測會影響較大 什麼是降維 降維是指在某些限定條件下,降低隨機變數(特徵)個數,得到一組“不
吳恩達機器學習(十二)主成分分析(降維、PCA)
目錄 0. 前言 學習完吳恩達老師機器學習課程的降維,簡單的做個筆記。文中部分描述屬於個人消化後的理解,僅供參考。 如果這篇文章對你有一點小小的幫助,請給個關注喔~我會非常開心的~ 0. 前言 資料的特徵數量,又稱作向量的維度。降維(dimens
降維(一) PCA
為什麼需要降維? \qquad如果我們希望模型的精度比較高,或者說泛化誤差率較小,那麼我們希樣本的取樣密度足夠大(密取樣),即在任意樣本xxx附近任意小的δ\deltaδ距離範圍內總能找到一個樣本。 \qquad假設所有樣本在其屬性上歸一化,對於δ=0.001\
機器學習--降維技術PCA
1.PCA降維原理: PCA屬於線性降維方式: X為原空間 W為變化矩陣 Z為新空間 Z的維數要小於X維數,實現了降維處理。 用一個超平面來表示正交屬性空間的樣本點,這個超平面應該儘量滿足最近重構性以及最大可分性,即空間中所有點離這個超平面儘可能近,樣本點
機器學習實戰(十二)降維(PCA、SVD)
目錄 0. 前言 學習完機器學習實戰的降維,簡單的做個筆記。文中部分描述屬於個人消化後的理解,僅供參考。 本篇綜合了先前的文章,如有不理解,可參考: 如果這篇文章對你有一點小小的幫助,請給個關注喔~我會非常開心的~ 0
資料降維(三)PCA主成分分析
文章目錄 PCA主成分分析 目標函式1:最小化重建誤差 目標函式2:最大化方差 PCA目標函式計算 求解PCA(1) 表現 求解PCA(2) PCA總結 PCA主成分分析 目標
『機器學習筆記 』GBDT原理-Gradient Boosting Decision Tree
1. 背景 決策樹是一種基本的分類與迴歸方法。決策樹模型具有分類速度快,模型容易視覺化的解釋,但是同時是也有容易發生過擬合,雖然有剪枝,但也是差強人意。 提升方法(boosting)在分類問題中,它通過改變訓練樣本的權重(增加分錯樣本的權重,減
特徵選擇與特徵降維的差別
在machine learning中,特徵降維和特徵選擇是兩個常見的概念,在應用machine learning來解決問題的論文中經常會出現。 對於這兩個概念,很多初學者可能不是很清楚他們的區別。很多人都以為特徵降維和特徵選擇的目的都是使資料的維數降
機器學習---降維之PCA主成分分析法
(一)、主成分分析法PCA簡介 PCA 目的:降維——find a low dimension surface on which to project data ~如圖所示,尋找藍色的點到
機器學習-->特徵降維方法總結
本篇博文主要總結一下機器學習裡面特徵降維的方法,以及各種方法之間的聯絡和區別。 機器學習中我個人認為有兩種途徑可以來對特徵進行降維,一種是特徵抽取,其代表性的方法是PCA,SVD降維等,另外一個途徑就是特徵選擇。 特徵抽取 先詳細講下PCA降維的原理
機器學習筆記(二)——廣泛應用於資料降維的PCA演算法實戰
最近在學習的過程當中,經常遇到PCA降維,於是就學習了PCA降維的原理,並用網上下載的iris.txt資料集進行PCA降維的實踐。為了方便以後翻閱,特此記錄下來。本文首先將介紹PCA降維的原理,然後進入實戰,編寫程式對iris.資料集進行降維。一、為什麼要進行資料降維?
降維演算法--PCA 與 t-SNE
PCA是大家所熟知的降維演算法,但是線性降維雖然簡單,其侷限性也很明顯,難以實現高維資料在低維空間的視覺化。t-SNE是非線性的降維演算法,能實現高維到低維的視覺化對映,但因為涉及大量的條件概率、梯度下降等計算,時間和空間複雜度是平方級的,比較耗資源。t-SNE幾乎可用於所有
吳恩達機器學習總結:第十一 降維(PCA)(大綱摘要及課後作業)
為了更好的學習,充分複習自己學習的知識,總結課內重要知識點,每次完成作業後都會更博。總結1.動機I:資料壓縮(1)壓縮 a.加速演算法 b.減小資料空間 c.2維降為1維例子 d.3維降為2維例子 e.在實際中,我們正常會將1000維將為1
