支援向量機（SVM）

SVM調參

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

import seaborn as sns;sns.set()
#先把可能或不一定用到的庫全導進來

from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)
plt.scatter(
 
X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')#先假設一堆資料，random_state為隨機種子

<matplotlib.collections.PathCollection at 0x1e4832b3be0>

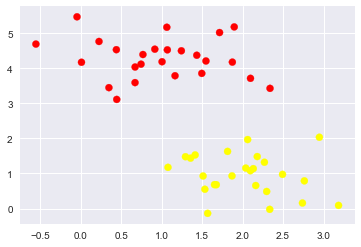
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.plot(xfit, xfit+0.65, '-k')
plt.plot(xfit, 0.5*xfit+1.6, '-k')
plt.plot(xfit, -0.2*xfit+
 
2.9, '-k')
plt.xlim(-1, 3.5)
#此處隨機畫出幾條線，大家可以判斷哪條線是理兩邊雷區都比較遠的，很明顯是中間那條對吧

(-1, 3.5)

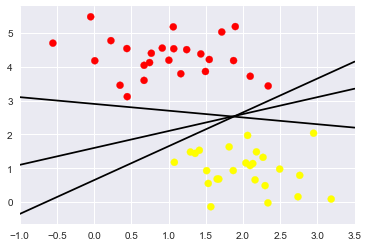
# 那麼我們來試一下是不是中間那條比較好呢
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
    yfit = m * xfit + b
    plt.plot(xfit, yfit,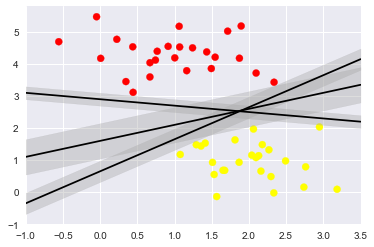
 
 '-k')
    plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
                     color='#AAAAAA', alpha=0.4)

plt.xlim(-1, 3.5);#可見中間那條的確比較好

訓練一個基本的SVM

from sklearn.svm import SVC # 這個是支援向量機分類器的意思support vector classifier
model = SVC(kernel='linear')
model.fit(X,y)

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='auto', kernel='linear',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)

#繪圖函式,不要深究，當模板用就可以了
def plot_svc_decision_function(model, ax=None, plot_support=True):
    """Plot the decision function for a 2D SVC"""
    if ax is None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    
    # create grid to evaluate model
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    Y, X = np.meshgrid(y, x)
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    P = model.decision_function(xy).reshape(X.shape)
    
    # plot decision boundary and margins
    ax.contour(X, Y, P, colors='k',
               levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--'])
    
    # plot support vectors
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0],
                   model.support_vectors_[:, 1],
                   s=300, linewidth=1, facecolors='none');
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model)#將剛剛那個模型傳進去，電腦會自動把線畫出來，找到那幾個支援向量

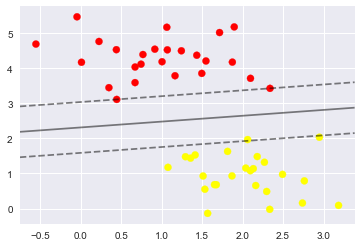
model.support_vectors_#這句可以直接打印出來模型裡面的支援向量是哪幾個

array([[0.44359863, 3.11530945],
       [2.33812285, 3.43116792],
       [2.06156753, 1.96918596]])

# 接下來我們構建更多的點的
# 構建之後我們發現，原來點的數目變多了，只要支援向量沒有發生變化，則畫出來的決策邊界也不會發生變化
def plot_svm(N=10, ax=None):
    X, y = make_blobs(n_samples=200, centers=2,
                      random_state=0, cluster_std=0.60)
    X = X[:N]
    y = y[:N]
    model = SVC(kernel='linear', C=1E10)
    model.fit(X, y)
    
    ax = ax or plt.gca()
    ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    ax.set_xlim(-1, 4)
    ax.set_ylim(-1, 6)
    plot_svc_decision_function(model, ax)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, N in zip(ax, [60, 120]):# 左邊那些點有60個，右邊的圖有120個
    plot_svm(N, axi)
    axi.set_title('N = {0}'.format(N))

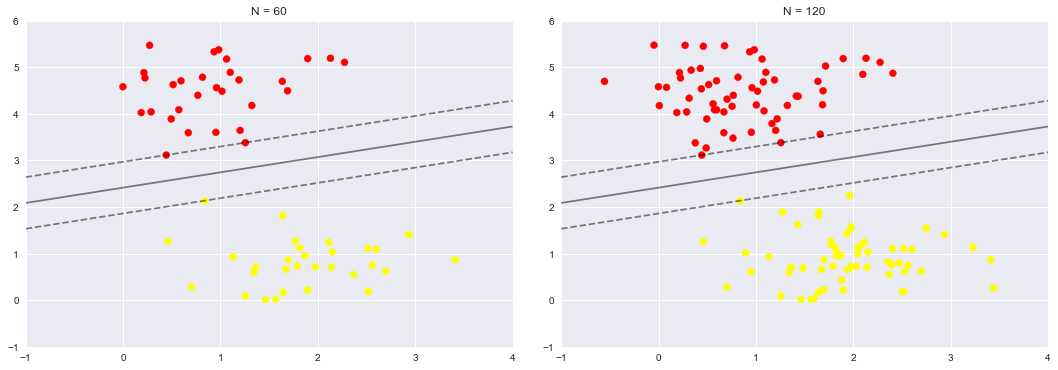
下面我們來看看對於下面這種非一刀就能分出來的情況怎麼處理呢

from sklearn.datasets.samples_generator import make_circles
X, y = make_circles(100, factor=.1, noise=.1)

clf = SVC(kernel='linear').fit(X, y)#線性的核函式

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf, plot_support=False);

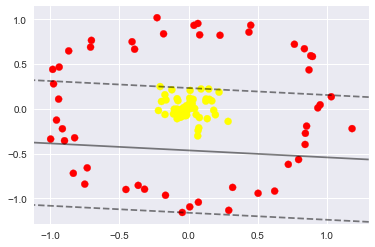
這種情況，線性的核函式已經解決不了了，那隻能試試高維的核變換了

#加入了新的維度r
from mpl_toolkits import mplot3d
r = np.exp(-(X ** 2).sum(1))
def plot_3D(elev=30, azim=30, X=X, y=y):
    ax = plt.subplot(projection='3d')
    ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn')
    ax.view_init(elev=elev, azim=azim)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('r')

plot_3D(elev=45, azim=45, X=X, y=y)#其實是人為地給分分顏色

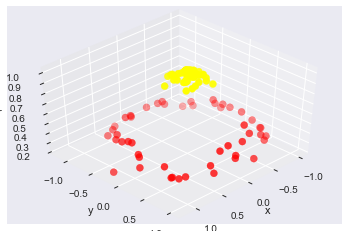
# 那麼我們試試引入一個徑向基函式
# 用上這個非線性核可以擬合出來更加奇怪的邊界形狀
clf = SVC(kernel='rbf',C=1E6)
clf.fit(X,y)

SVC(C=1000000.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
            s=300, lw=1, facecolors='none');

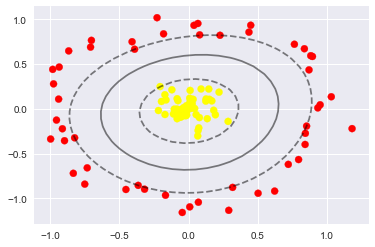
調節SVM引數: Soft Margin問題

調節C引數

• 當C趨近於無窮大時：意味著分類嚴格不能有錯誤
• 當C趨近於很小的時：意味著可以有更大的錯誤容忍

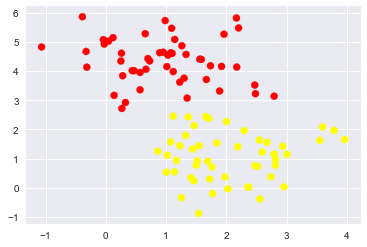
# 我們再創造一組資料，這組資料中離散程度更大，兩堆資料近乎貼在一起
X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn');

X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=0.8)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

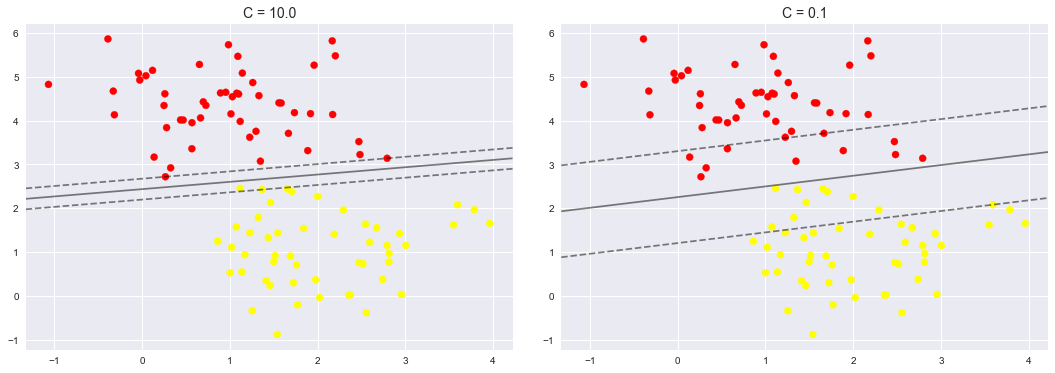
for axi, C in zip(ax, [10.0, 0.1]):# 我們定義兩種C引數，一個是10， 一個是0.1，可以看出，C=0.1的時候決策邊界允許容納更多的錯誤
    model = SVC(kernel='linear', C=C).fit(X, y)
    axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_svc_decision_function(model, axi)
    axi.scatter(model.support_vectors_[:, 0],
                model.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none');
    axi.set_title('C = {0:.1f}'.format(C), size=14)

X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=1.1)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

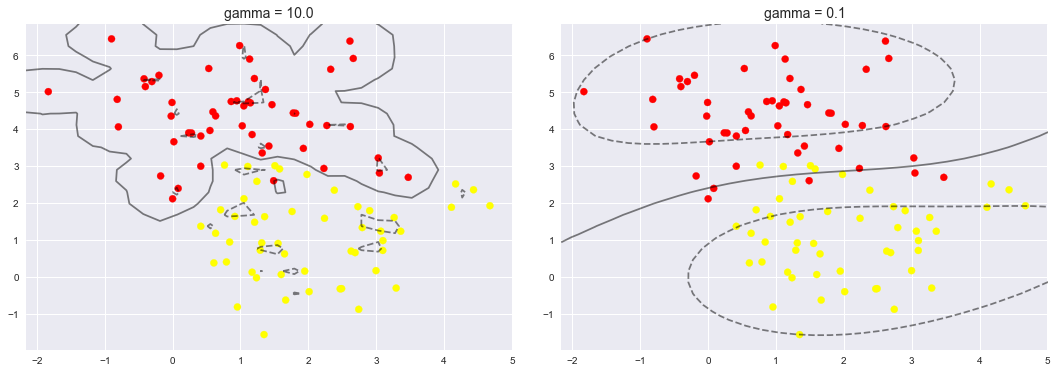
for axi, gamma in zip(ax, [10.0, 0.1]):
    model = SVC(kernel='rbf', gamma=gamma).fit(X, y)# 這裡的高斯核函式裡指定了不同的gamma值，gamma值越大，決策邊界越複雜
    # 但是比如圖一這種，其實使用價值不高的，因為屬於過擬合了，很難泛化，也就是真正利用起來的時候不一定就很準
    axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_svc_decision_function(model, axi)
    axi.scatter(model.support_vectors_[:, 0],
                model.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none');
    axi.set_title('gamma = {0:.1f}'.format(gamma), size=14)

對唐宇迪老師的機器學習教程進行筆記整理
編輯日期：2018-10-9
小白一枚，請大家多多指教
轉載請註明出處