cdq分治淺談
$cdq$分治淺談
1.分治思想
分治實際上是一種思想,這種思想就是將一個大問題劃分成為一些小問題,並且這些小問題與這個大問題在某中意義上是等價的。
2.普通分治與$cdq$分治的區別
普通分治與$cdq$分治都是基於分治思想之上的演算法,但是他們是有區別的。普通分治的適用條件是,產生的小問題之間互不影響,然而$cdq$分治就相對比較寬泛,小問題之間可以有影響,但是$cdq$分治不支援強制線上。
3.$cdq$分治淺談
分治一共分為四步:
1) 將當前處理區間分為左右兩個等大的子區間;
2) 遞迴處理左子區間;
3) 處理左區間對於右區間的影響,並對於右區間或者答案進行更改與修正;
4) 遞迴處理右子區間;
上面就是$cdq$分治的四個步驟,這四個步驟之中第一、二、四步對於不同的題目來說基本上是相同的,因為畢竟分割槽間,遞迴沒有什麼好更改的。對於不同的題目來說不同點就是第三部,這一步也是$cdq$分治的難點,對於這一步的講解也要藉助於例題。
4.例題
題目描述:對於序列$A$,它的逆序對數定義為滿足$i<j$,且$A_i>A_j$的數對$(i,j)$的個數。給1到n的一個排列,按照某種順序依次刪除m個元素,你的任務是在每次刪除一個元素之前統計整個序列的逆序對數。
輸入格式:輸入第一行包含兩個整數$nm$和$mn$,即初始元素的個數和刪除的元素個數。以下$n$行每行包含一個$1$到$n$之間的正整數,即初始排列。以下$m$行每行一個正整數,依次為每次刪除的元素。$N\le100000 ,M\le50000。$
輸出格式:輸出包含$m$行,依次為刪除每個元素之前,逆序對的個數。
思路:首先我們對於這個問題可以轉化為二維數點問題,我們將每一個數字的編號作為橫座標,數字本身作為縱座標標記在平面直角座標系裡,這樣我們就可以將每一個點所包含的逆序對數轉化為數點問題。例如:3 4 2 1 5,這個序列被轉化為圖形之後就是下圖的樣子:
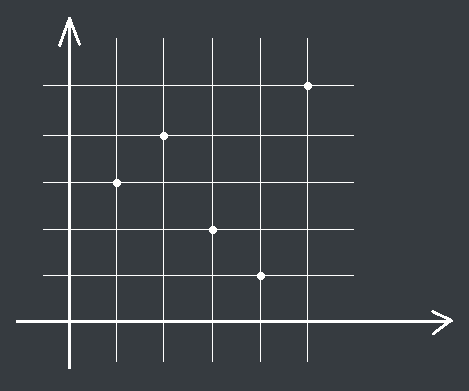
我們發現上面的有一個規律,對於第三個位置上的二,共參與了三個逆序對。分別為第一個數字,第二個數字和第四個數字。這三個數字對於第三個數字來說都有一個共同的性質,他們都在三號點的左上方和右下方,由於本題是$n$的全排列,且所有數字的編號都不能超過$n$,所以對於當前狀態下的數列中的$i$號點來說他參與的逆序對總數,就是由$(0,A_i)$和$(i,n)$圍成的矩形中的點數加上由$(i,0)$和$(n,A_i)$圍成的矩形中的點數。這樣我們就能統計出來每一個點當前參與的逆序對數,對於當前刪點後的答案,就是上一個狀態減去當前點所參與的逆序對數。
對於刪除操作來說,我們只需要進行賦值就可以了。開始的時候我們將所有的點都賦值成為1,刪除的時候就是將當前的賦值成為0。這樣矩形內數點就是矩形內統計權值和,這樣我們就完成了問題的轉化。顯然轉化成為的問題可以運用$KDtree$來完成,下面講解一下$cdq$做法。
對於對點賦值,我們可以轉化為對點加值,及加上$\Delta$。我們定義兩種操作,$oper=1$的操作中有三個值$x,y,z$,表示將位置為$(x,y)$的點的權值加上$z$。$oper=2$的操作中有四個值$x,y,z,id$,表示統計由$(0,0)$和$(x,y)$圍成的矩形中的權值和,並將這個權值和乘上係數$z$加到編號為$id$的答案陣列上。對於每一個操作我們都加上一個引數$ord$,表示這個操作的新增順序。(注:對於每一個矩形的詢問操作,我們都能轉化為$oper=2$的加減,運用容斥,即可。)
我們將這些操作進行排序,第一關鍵字是$x$,第二關鍵字是$y$。然後就是$solve$。因為更改操作會影響到查詢操作,所以$ord$小的點會影響到$ord$大的點,這樣的話我們的分治區間就是操作的$ord$編號。我們將$ord$小的點放在左面,$ord$大的放在右面,並且我們不要更改在$solve$之前排序後的相對位置,這樣我們的左右區間內依舊保證最開始的相對順序。
我們在分劃之後就可以遞迴了,我們先遞迴左區間,在遞迴完成之後我們就要處理左區間對於右區間的影響,影響主要在於左區間的修改和右區間的查詢。因為我們的左右區間在劃分之前是按照最開始的關鍵字進行的排序,並且最開始的排序方式我們可以用樹狀陣列進行統計答案,但是後來劃分的順序不能,所以本題的步驟順序有所改變,即先統計左區間對於右區間的影響,後進行左右兩個區間的遞迴處理。
下面是程式碼:可以結合程式碼和上面的描述進行理解。
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 100010
int n,m,idx,place[N],tmp[N];long long ans[N];
struct Oper {int kind,x,y,z,ord,id;}oper[N<<3],tmpx[N<<3];
bool cmp(const Oper &a,const Oper &b)
{return (a.x==b.x&&a.y==b.y)?(a.ord<b.ord):((a.x==b.x)?(a.y<b.y):(a.x<b.x));}
void add(int x,int y) {while(x<=n) tmp[x]+=y,x+=x&-x;}
int find(int x) {int tmp1=0;while(x) tmp1+=tmp[x],x-=x&-x;return tmp1;}
void solve(int l,int r)
{
if(l==r) return;
int mid=(l+r)>>1,tl=l-1,tr=mid;
for(int i=l;i<=r;i++)
{
if(oper[i].ord<=mid&&oper[i].kind==1) add(oper[i].y,oper[i].z);
if(oper[i].ord>mid&&oper[i].kind==2) ans[oper[i].id]+=find(oper[i].y)*oper[i].z;
}
for(int i=l;i<=r;i++)
if(oper[i].ord<=mid&&oper[i].kind==1) add(oper[i].y,-oper[i].z);
for(int i=l;i<=r;i++)
{
if(oper[i].ord<=mid) tmpx[++tl]=oper[i];
else tmpx[++tr]=oper[i];
}
for(int i=l;i<=r;i++) oper[i]=tmpx[i];
solve(l,mid),solve(mid+1,r);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1,a;i<=n;i++)
{
scanf("%d",&a),oper[++idx].kind=1,oper[idx].x=i;
oper[idx].y=a,oper[idx].z=1,oper[idx].ord=idx,place[a]=i;
add(a,1),ans[1]+=i-find(a);
}
for(int i=1;i<=n;i++) add(i,-1);
for(int i=1,a;scanf("%d",&a),i<=m;i++)
{
oper[++idx].kind=2,oper[idx].x=place[a],oper[idx].y=n;
oper[idx].z=-1,oper[idx].ord=idx,oper[idx].id=i+1;
oper[++idx].kind=2,oper[idx].x=n,oper[idx].y=a;
oper[idx].z=-1,oper[idx].ord=idx,oper[idx].id=i+1;
oper[++idx].kind=2,oper[idx].x=place[a],oper[idx].y=a;
oper[idx].z=2,oper[idx].ord=idx,oper[idx].id=i+1;
oper[++idx].kind=1,oper[idx].x=place[a],oper[idx].y=a,oper[idx].z=-1,oper[idx].ord=idx;
}sort(oper+1,oper+idx+1,cmp),solve(1,idx);
for(int i=2;i<=m;i++) ans[i]+=ans[i-1];
for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
}
題目描述:有n朵花,每朵花有三個屬性:花形$(s)$、顏色$(c)$、氣味$(m)$,用三個整數表示。現在要對每朵花評級,一朵花的級別是它擁有的美麗能超過的花的數量。定義一朵花A比另一朵花B要美麗,當且僅當$S_a\ge S_b$,$C_a\ge C_b$,$M_a\ge M_b$。顯然,兩朵花可能有同樣的屬性。現在需要統計出評出每個等級的花的數量。
輸入格式:第一行為$N,K (1 \le N \le 100,000, 1 \le K \le 200,000 )$, 分別表示花的數量和最大屬性值。以下$N$行,每行三個整數$s_i, c_i, m_i (1 \le s_i, c_i, m_i \le K)$,表示第$i$朵花的屬性。
輸出格式:包含$N$行,分別表示評級為$ 0 … N-1 $的每級花的數量。
思路:首先這道題就是三維偏序的題,我們考慮將每一朵花的三個屬性作為三維座標的第一位,第二維,第三維。例如:1朵花屬性分別為:$(3,3,3)$就可以變成下面的樣子。

顯然滿足花$A$比花$B$美麗的條件是在轉化完圖形之後點$B$要在點$A$和原點圍成的三維圖形裡面。這個問題顯然能用$KDtree$來解決。下面來講解cdq的做法。
因為這些花之間只有這三個性質來要求,所以我們就沒有必要來按照讀入順序來處理。我們將第一個屬性作為第一關鍵字,第二個屬性作為第二個關鍵字,第三個屬性作為第三個關鍵字進行排序。排序之後相同的花就在一起了,這時我們進行去重,由於我們按照第一關鍵字已經排序了,所以是不是就轉化成為上面那道題的思路了?只是查詢沒有那麼毒瘤而已。
上面兩到例題都是數點問題,同樣的型別題還有:bzoj1935[Shoi2007]Tree園丁的煩惱、bzoj2683簡單題、bzoj1176[Balkan2007]Mokia。
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 100010
int n,m,tmp[N<<1],ans[N];
struct Flower {int x,y,z,man,hav,id;}flower[N];
bool cmp(const Flower &a,const Flower &b)
{return (a.x!=b.x)?(a.x<b.x):((a.y!=b.y)?a.y<b.y:a.z<b.z);}
bool cmp2(const Flower &a,const Flower &b)
{return (a.y!=b.y)?(a.y<b.y):((a.z!=b.z)?a.z<b.z:a.x<b.x);}
void add(int x,int y) {while(x<=m) tmp[x]+=y,x+=x&-x;}
int find(int x) {int tmp1=0;while(x) tmp1+=tmp[x],x-=x&-x;return tmp1;}
void solve(int l,int r)
{
if(l==r) return;
int mid=(l+r)>>1;
solve(l,mid),solve(mid+1,r),sort(flower+l,flower+r+1,cmp2);
for(int i=l;i<=r;i++)
{
if(flower[i].id<=mid) add(flower[i].z,flower[i].hav);
else flower[i].man+=find(flower[i].z);
}
for(int i=l;i<=r;i++)
if(flower[i].id<=mid) add(flower[i].z,-flower[i].hav);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d%d",&flower[i].x,&flower[i].y,&flower[i].z);
sort(flower+1,flower+n+1,cmp);int cnt=0;
for(int i=1;i<=n;flower[cnt].hav++,i++)
if(flower[i].x!=flower[i-1].x||flower[i].y!=flower[i-1].y||flower[i].z!=flower[i-1].z)
flower[++cnt]=flower[i],flower[cnt].id=cnt,flower[i].hav=flower[i].man=0;
solve(1,cnt);
for(int i=1;i<=cnt;i++) ans[flower[i].man+flower[i].hav-1]+=flower[i].hav;
for(int i=0;i<=n-1;i++) printf("%d\n",ans[i]);
}
思路:首先,我們能想到這道題是一道$dp$題目,我們設$f[i]$表示第$i$天能得到的最大收益,這個最大收益也包括第$i$天不進行操作的情況下的收益,設$X[i]$表示第$i$天將所有的現金都兌換成為金券後能拿到的$A$券數,$Y[i]$同理。這是我們發現一個轉移式子:$f[i]=Max\{f[i-1],A[i]\times X[j]+B[i]\times Y[j]\}\ (1\le j \le i-1)$。我們發現這個式子能寫成斜率優化的樣子:$Y[j]=-\frac{A[i]}{B[i]}\times X[j]+\frac{f[i]}{B[i]}$。我們考慮一下能否運用斜率優化,好像可以,對於每一個點的斜率$k$為$-\frac{A[i]}{B[i]}$,橫座標為$X[i]$,縱座標為$Y[i]$。但是就是有兩個不太好的情況,就是每一點的$x$座標與斜率$k$都不單調,這個怎麼辦?顯然用平衡樹維護凸包就好了。我們考慮一下不用平衡樹能否實現,我們考慮$cdq$。
因為正常的要求最大值的斜率優化都是橫座標單調遞增,斜率單調遞減,所以我們考慮排序。因為每一個點的斜率都是不變的,即輸入之後就是定下來的,所以我們可以將這些所有的點都按照斜率遞減排序,但是這樣就不是按照天數遞增的順序了,所以我們就不能直接運用排序後的順序來處理這些點。我們將天數進行分治,這樣的話我們每一個點就需要再存一個引數,即天數的編號。
因為這是$dp$,所以我們在遞迴左區間之後顯然要先處理影響,再遞迴右區間。現在考慮怎麼處理影響。
因為我們每一次處理影響之前都已經處理好左區間了,所以我們現在可以不用理會左區間的具體順序了,這樣的話我們就能對其進行任意順序的處理,我們可以將左區間的這些點按照橫座標排序,這樣我們就能夠達到上面所提出的目的,也就是把點按照順序插入到凸包裡面。因為我們是用左區間來更新右區間,所以我們不用去管右區間,並且因為右區間的斜率是單調遞減的,所以我們可以按照右區間原本的順序來進行更新。
我們在遞迴出口的地方不能就是直接$return$,我們需要做一些小小的處理,因為我們在$return $之前這個點一定已經做完前面的點的所有更新了,但是沒有進行不作處理的更新,所以$f[i]=Max\{f[i],f[i-1]\}$。至此搜有的更新都完成了,這是就可以了處理當前點的橫縱座標。因為必然存在一種最優的買賣方案滿足:每次買進操作使用完所有的人民幣;每次賣出操作賣出所有的金券,所以當前點的橫縱座標就是$X[i]=\frac{f[i]}{A[i]*Rate[i]+B[i]}\times A[i]$,$Y[i]=\frac{f[i]}{A[i]*Rate[i]+B[i]}$。
對於橫座標排序,我們顯然沒有必要每一次都用$sort$,我們運用歸併排序的思想,直接排序即可,時間複雜度會降下$O(log_n)$。
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 100010
#define eps 1e-9
int n,que[N];double f[N];
struct Node {double a,b,rate,k,x,y;int id;}node[N],tmp[N];
bool cmp(const Node &a,const Node &b) {return a.k>b.k;}
double re_x(int i) {return node[i].x;}
double re_y(int i) {return node[i].y;}
double re_k(int i,int j)
{
if(fabs(node[i].x-node[j].x)<eps)return 1e20;
return (re_y(j)-re_y(i))/(re_x(j)-re_x(i));
}
void solve(int l,int r)
{
if(l==r)
{
f[l]=max(f[l],f[l-1]);
node[l].y=f[l]/(node[l].a*node[l].rate+node[l].b);
node[l].x=node[l].y*node[l].rate;return;
}
int mid=(l+r)>>1,tl=l-1,tr=mid;
for(int i=l;i<=r;i++) (node[i].id<=mid)?tmp[++tl]=node[i]:tmp[++tr]=node[i];
for(int i=l;i<=r;i++) node[i]=tmp[i];solve(l,mid);
int L=1,R=0;
for(int i=l;i<=mid;i++)
{while(R>1&&re_k(que[R],que[R-1])<re_k(que[R],i)+eps) R--;que[++R]=i;}
for(int i=mid+1;i<=r;i++)
{
while(L<R&&re_k(que[L],que[L+1])+eps>node[i].k) L++;
f[node[i].id]=max(f[node[i].id],node[que[L]].x*node[i].a+node[que[L]].y*node[i].b);
}solve(mid+1,r),tl=l,tr=mid+1;
for(int i=l;i<=r;i++)
{
if((node[tl].x<node[tr].x||tr>r||fabs(node[tl].x-node[tr].x)<eps)&&tl<=mid)
tmp[i]=node[tl++];
else tmp[i]=node[tr++];
}
for(int i=l;i<=r;i++) node[i]=tmp[i];
}
int main()
{
scanf("%d%lf",&n,&f[0]);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf%lf",&node[i].a,&node[i].b,&node[i].rate);
node[i].k=-node[i].a/node[i].b,node[i].id=i;
}sort(node+1,node+n+1,cmp),solve(1,n),printf("%.3lf\n",f[n]);
}
