[機器學習] 貝葉斯分類器1
阿新 • • 發佈:2019-01-11
貝葉斯分類的先導知識
條件概率
所謂條件概率,它是指某事件B發生的條件下,求另一事件A的概率,記為,它與是不同的兩類概率。
舉例: 考察有兩個小孩的家庭, 其樣本空間為, 其中b 代表男孩,g代表女孩,bg表示大的是男孩、小的是女孩,其它點可類似說明
在 中4個樣本點等可能的情況下,我們來討論一些事件的概率。
- 事件 A = “家中至少有一個女孩”發生的概率為
- 若已知事件 B = “家中至少有一個男孩” 發生, 再求事件 A 發生的概率為
這是因為事件B的發生,排除了gg發生的可能。這是樣本空間也隨之改為 , 而在中事件A中只含2個樣本點,故。這就是條件概率,它與無條件概率是不同的兩個概念。 - 若對上述條件概率的分子分母各除以4, 則可得
其中交事件AB = “家中既有男孩又有女孩”。這個關係具有一般性,也就是說,條件概率是兩個無條件概率之商。
全概率公式
全概率是概率論中一個重要的公式, 它提供了計算複雜事件概率的一條有效途徑,使一個複雜事件的概率計算問題化簡就繁。
性質:設為樣本空間的一個分割,即互補相容,且,如果, i = 1, 2, ..n, 對任一事件A有
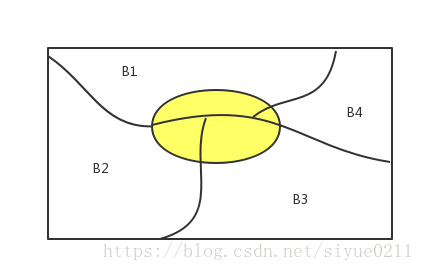
證明:因為
且互不相容,所以由可加得
