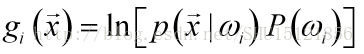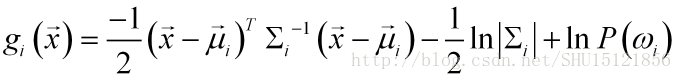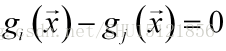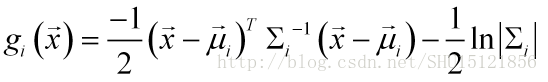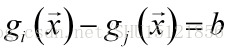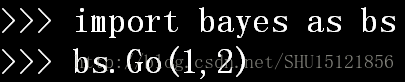【ML學習筆記】17:多元正態分佈下極大似然估計最小錯誤率貝葉斯決策
阿新 • • 發佈:2019-01-11
簡述多元正態分佈下的最小錯誤率貝葉斯
如果特徵的值向量服從d元正態分佈,即其概率密度函式為:
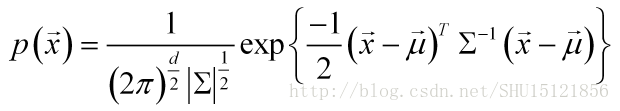
即其分佈可以由均值向量和對稱的協方差矩陣
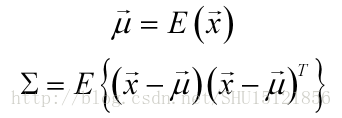
唯一確定。
如果認為樣本的特徵向量在類內服從多元正態分佈:
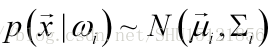
即對於每個類i,具有各自的類內的均值向量和協方差矩陣。
如之前所學,最小錯誤率貝葉斯的判別函式的原始形式是:
類條件概率密度服從多元正態分佈,帶入,得:
因為是比較大小用的,去掉與類號i無關的項:
而用於分類的決策面是:
在實際問題下的措施
①反向判別
這次要做的還是用[身高,體重,鞋碼]->[性別]的資料,認為類別男女出現的次數一樣,即先驗概率都是0.5,則可以在判別函式中去除這一項:
判別函式僅僅是比較大小用的,為了減少計算機計算量,改用反向判別的函式:
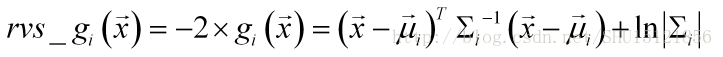
反向判別函式則要取函式值小的那一方作為預測的類別。
②分類面取樣以對ROC上取樣點做估計
對於多元正態分佈,用理論公式的方式(多重積分)去計算錯誤率是很困難的,所以繪製ROC曲線時,我採用改變分類面,獲得多個取樣分類面,在取樣分類面上用頻率估計錯誤率。
改變取樣分類面的方式可以改變分類面的常數閾值,即把0改成一定區間上的正負值b:
程式碼實現
#-*-coding:utf-8-*-
from numpy import *
import operator
from matplotlib import 測試
直接用封裝好的演示用的函式演示功能:
import bayes as bs
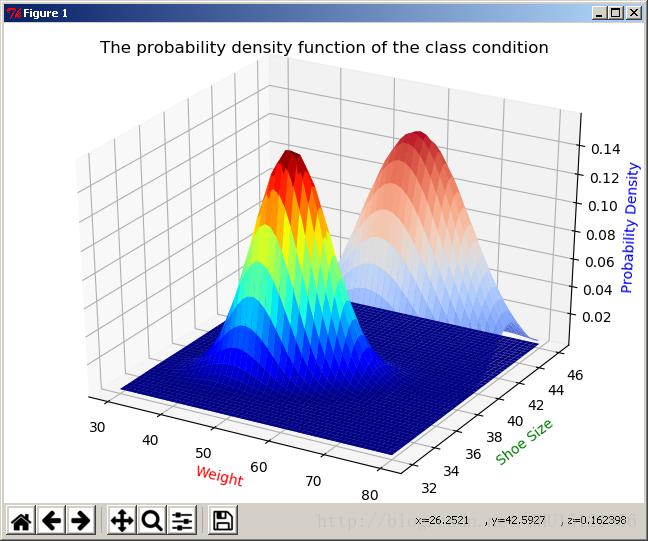
bs.Go(1,2)類條件概率密度函式圖:
關閉視窗後開始取樣繪製ROC:
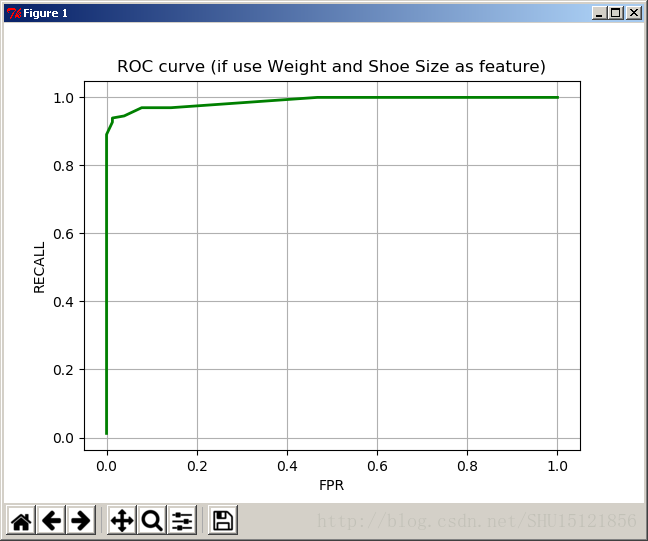
繪製好的ROC曲線:
與一元情況的比較
在上篇中,僅使用身高或者僅使用體重做判別,得到的分類器效果都很不好。從常理上也能解釋,身高或者體重都不是鑑別男女的有效手段。建立好這個分類器後,可以看看這兩個特徵聯合的分類效果如何。
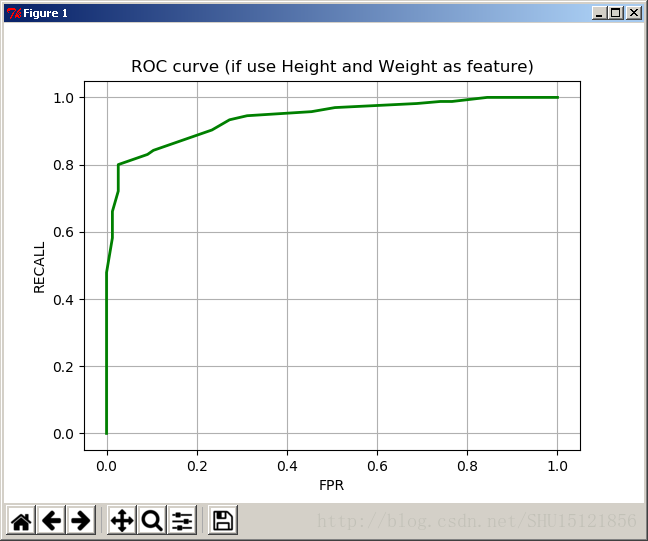
看似不那麼合適的兩個特徵,聯合後的分類效果好了很多。