opengl的GL_PROJECTION變換矩陣
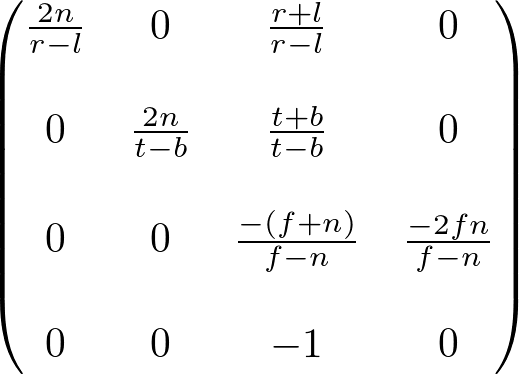
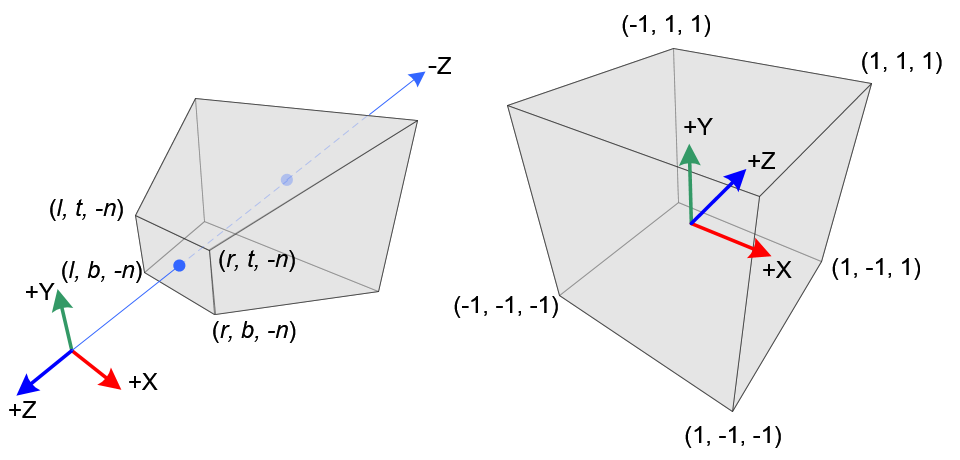
攝像頭座標系的形狀如下圖第一個, 是一個平截頭體。
x軸方向上定義 r: right , l: left, y軸方向上定義 t: top, b: bottom, z軸方向上定義 n: near, f: far。
每個攝像頭根據焦距的不同,對應的上面的值也會有差別。根據實際情況調整數值。
下圖的第二個座標系就是標準座標系:NDC(normalized device coordinates),是opengl初始的座標系。
計算該變換矩陣的原理如下:
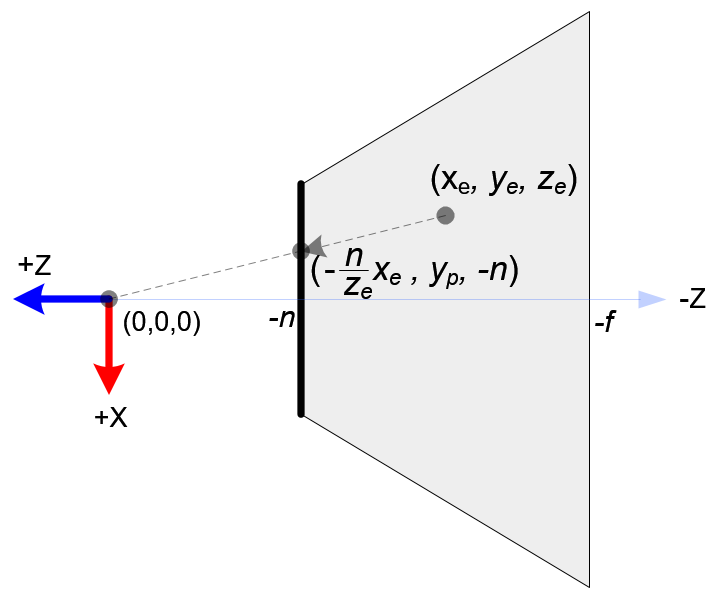
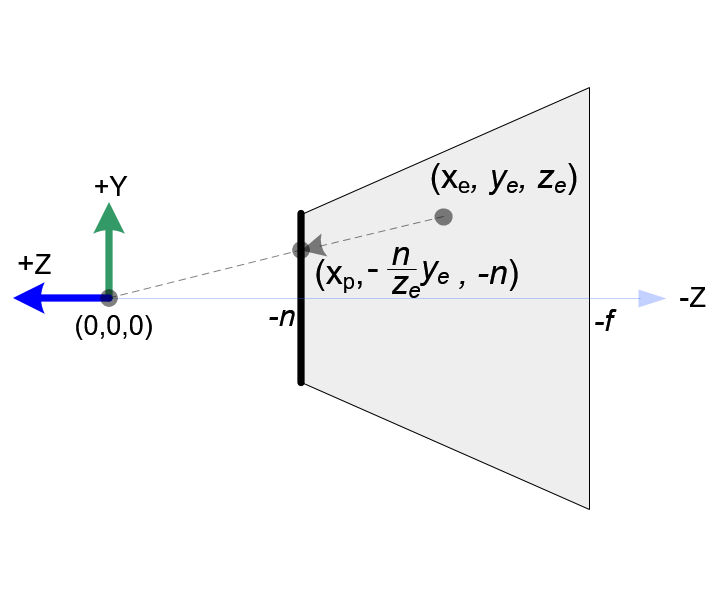
假設攝像頭座標系內有一個點(e),則該點在 -n 這個平面上的 X,Y 座標投影可以通過比例計算出來。
(攝像頭座標系,攝像頭所在座標為原點。這是opengl強制要求)
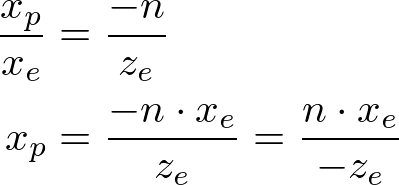
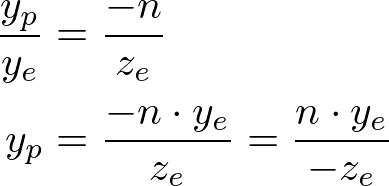
然後將 -n平面中X,Y 投影點 對映到 NDC 中,比如X 座標為: [l, r] ⇒ [-1, 1] ,通過線性關係,計算出在NDC的位置
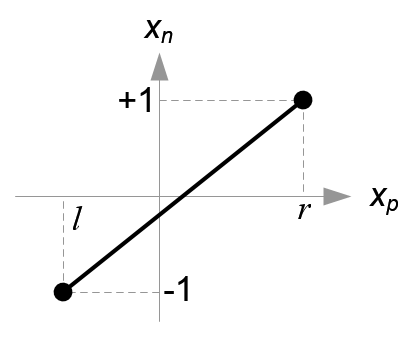
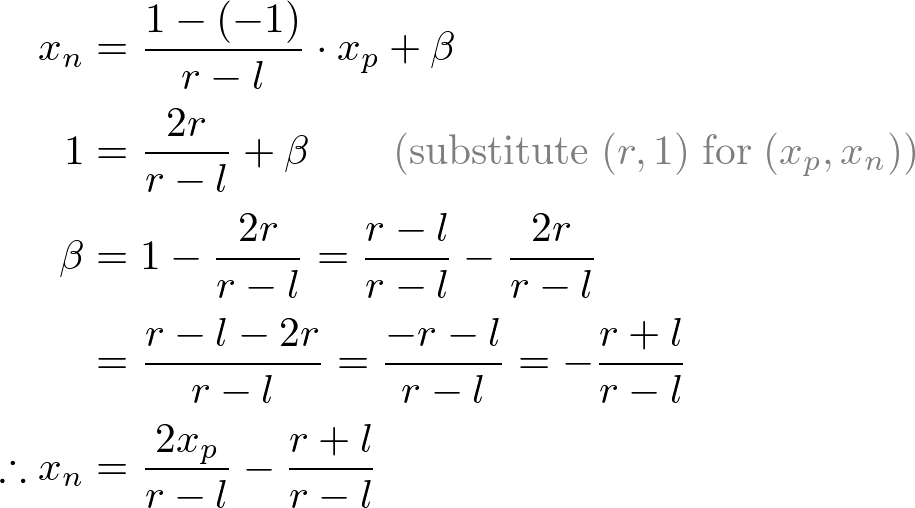
Y軸座標變換為:[b, t] ⇒ [-1, 1], 其 計算方式與X軸一樣,不再重複說明。
最終合併後,將 e 從 攝像頭座標系轉到 NDC的 表示式為:
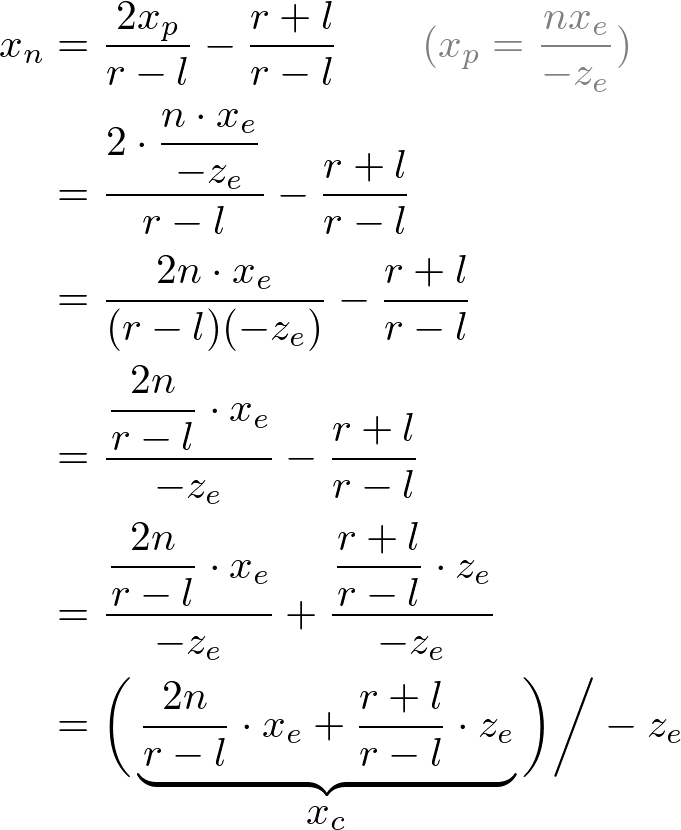
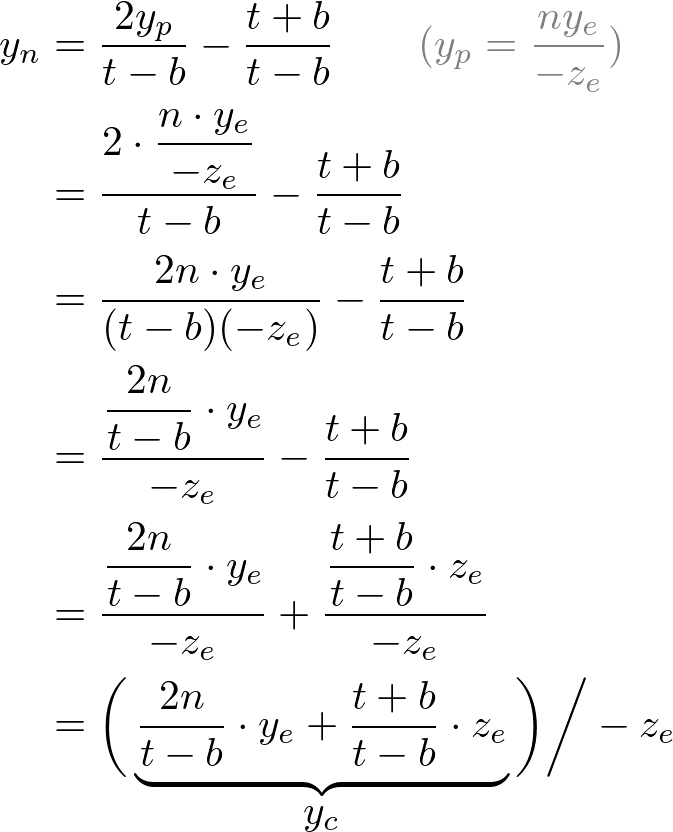
根據上面的公式,我們看到都需要 除以 -ze
我們可以將Wc 的值設為-ze。 (W 數值的作用: 如果W不為0, 那麼使用四維向量表示的3維座標是: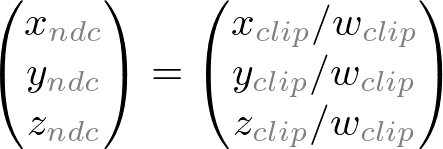 )
)
因此,我們就可以得到變換矩陣的部分數值。
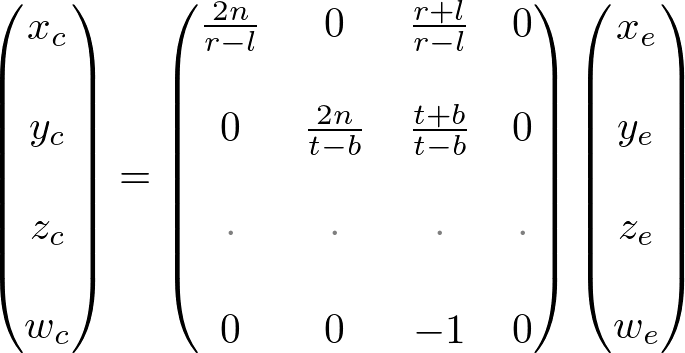
剩餘 Z 軸座標的變換,Z軸座標用於 裁剪 和 深度測試。 Z軸座標不依賴於 X,Y軸。因此假設Zn 與Ze 和 We相關,引數設為A,B
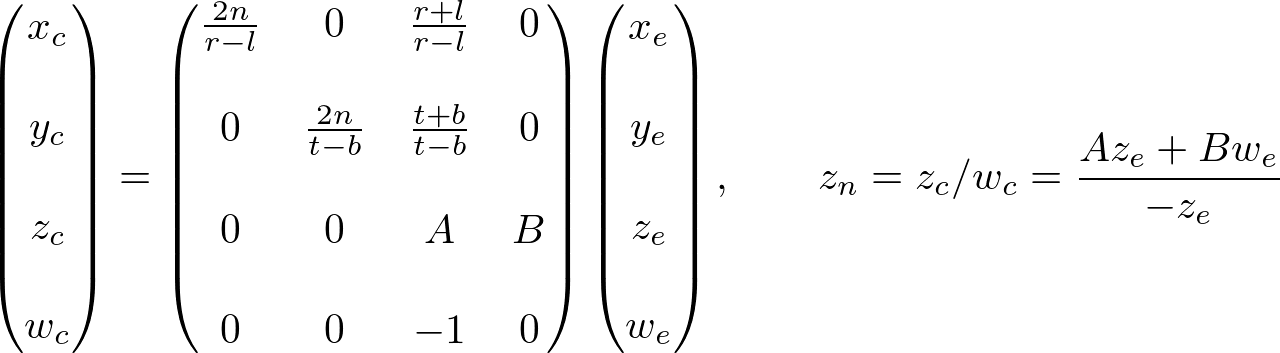
在 攝像頭座標系中 ,We 數值為1(X,Y, Z就是真正的座標位置)。
為了計算A和B 的值, 使用(ze, zn) 對映關係 (-n, -1) and (-f, 1)。
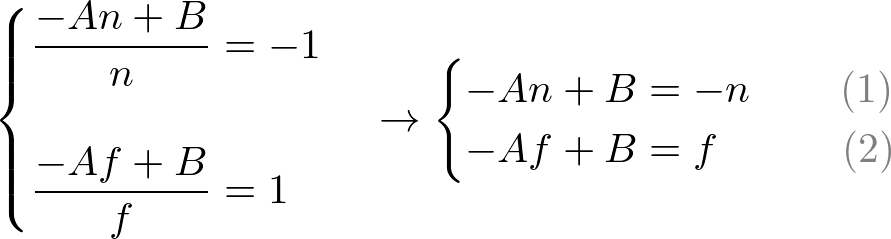
通過計算方程式,最終得到上面的變換矩陣。
(注: 此篇內容參考網頁: http://www.songho.ca/opengl/gl_projectionmatrix.html)
