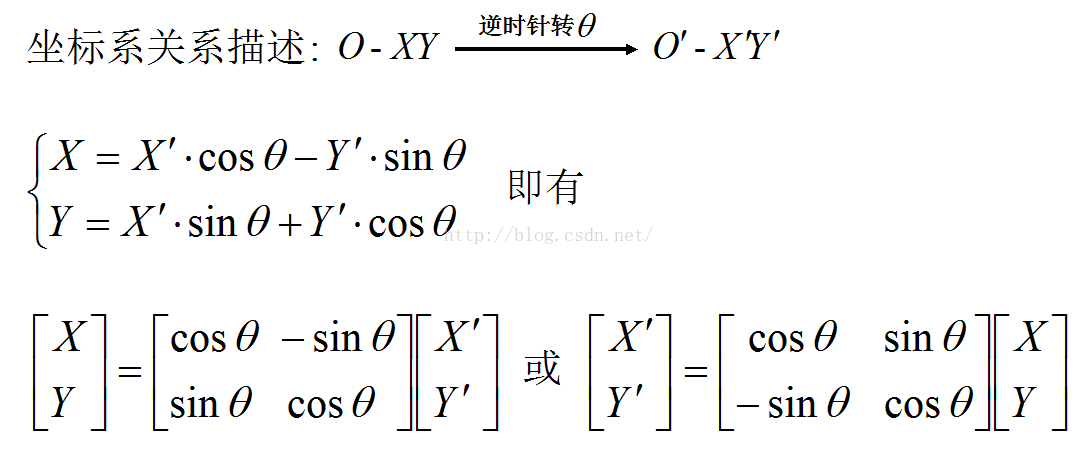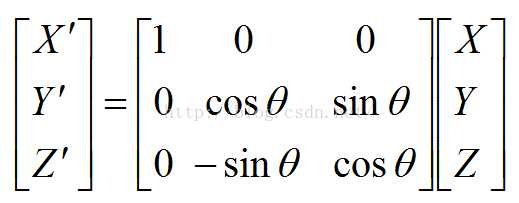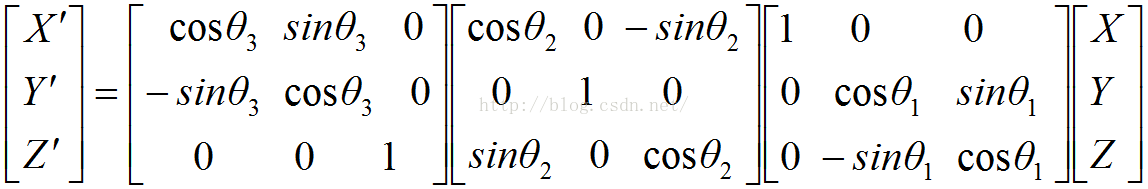在攝影測量和計算機視覺中，經常會遇到空間座標系之間的座標轉換問題，而兩個座標系之間的變換關係一般可以通過一個旋轉矩陣R和一個平移向量T（或C）描述。因此，理解清楚座標系之間旋轉平移的轉換過程與對應變換矩陣之間的關係十分重要。這個變換過程雖然簡單，但是其間涉及到的引數的表述存在多種形式，常常失之毫厘謬以千里，給我們的理解和使用帶來諸多不便，例如，旋轉角正方向的定義，不同座標軸的旋轉順序對應的旋轉矩陣的計算方法等等細節問題。本文將從基本的公式推導以及引數的準確描述出發，演算出我們常見的公式和結論。

一 僅存在旋轉關係

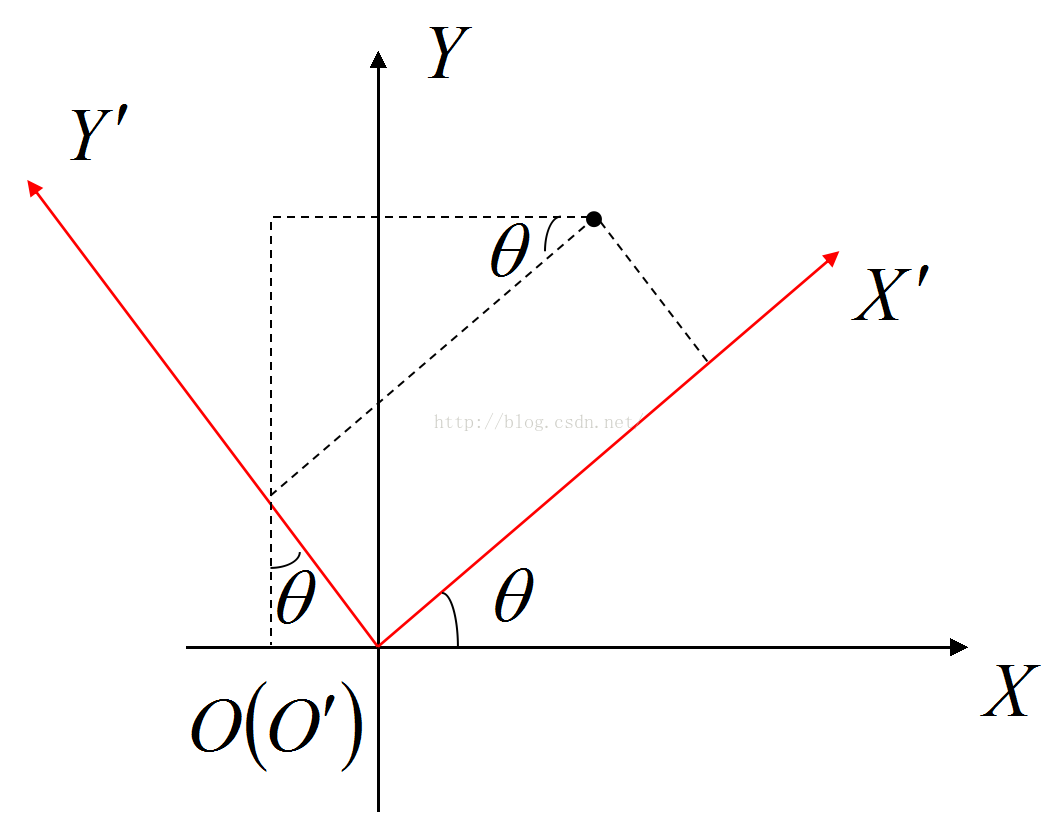
為了便於表述和分析，我們從平面直角座標系出發，座標系O-XY和座標系O'-X'Y'的關係如下圖所示：

對於以上座標關係，我們可以作如下描述：座標系O-XY逆時針旋轉theta（或順時針旋轉-theta）後與座標系O'-X'Y'重合，或者座標系O‘-X’Y‘順時針旋轉theta（或逆時針旋轉-theta）後與座標系O-XY重合。利用簡單的之間三角形的餘弦定理和正玄定理就可以得到以下公式（格式編輯不太熟，故以影象代替）：

至此，我們可以將2D平面的旋轉問題提升到3D空間的旋轉問題，即分別繞三個軸作類似2D的旋轉變換。需要額外注意的兩個的問題是：1）當繞某根軸旋轉時，其他兩軸建立的2D座標系應該保證旋轉軸的正方向垂直紙面向外（與旋轉角正方向定義相關）；2）空間座標系的旋轉關係與各座標軸的旋轉順序相關；假設兩個空間座標系O-XYZ與O'-X'Y'Z'之間只存在一個座標軸的旋轉，若座標系O-XYZ繞自身的X軸逆時針轉theta之後與座標系O’-X'Y'Z'重合，空間中某點M在座標系O-XYZ和O'-X'Y'Z'中的座標描述存在以下關係：

同理，若座標系O-XYZ繞自身的Y軸或Z軸逆時針轉theta之後與座標系O’-X'Y'Z'重合，則對應的座標關係如下：

我們注意到，與X和Z軸不同，當繞Y軸逆時針旋轉theta角時，對應的旋轉矩陣中帶負號元素變成了右上角的”sin“元素。原因在於根據上文提到的注意點1）建立的2D座標系縱軸是X軸，橫軸是Z軸，而座標向量的座標分量順序是X,Y,Z，所以得到的X和Z的座標關係需要調整一下順序，即可得到上面顯示的結果。

可以證明（具體證明過程可以查文獻）：對於存在任意旋轉變換的兩個空間座標系O-XYZ和O'-X'Y'Z'，可以通過依次繞三個座標軸旋轉一定角度實現兩個座標系對應座標軸的重合。這裡，我們假設座標系O-XYZ依次繞自身X軸、Y軸、Z軸分別逆時針轉theta1，theta2，theta3後可以與座標系O'-X'Y'Z'重合，則空間中某點M在這兩個座標系中的描述關係如下：

類似地，三個座標軸之間的其他旋轉順序組合可以進行類似的推導。

角度 無論正負，大小都能用。

https://blog.csdn.net/haiying2016/article/details/77685459

旋轉變換（一）旋轉矩陣

參考文獻：

Wiki Rotation (mathematics)
Euler’s rotation theorem