/刪除操作的BUG已經修復 /
最大堆、最小堆是一種用可用陣列儲存，並模擬實現二叉樹的資料結構。
最大（小）堆具有以下的顯著性質：
●最大（小）堆是一棵樹，且是完全二叉樹。
●最大（小）堆是每個根節點都一定大（小）於等於其子節點。
●在具體的儲存時陣列的[0]位置存放一個哨兵元素用於插入時防止越界，且由於這是 一棵完全二叉樹，位於[i]的節點其對應的父節點剛好是[i/2]。
●這裡討論的是二叉堆，以下程式碼對應二叉堆的性質。

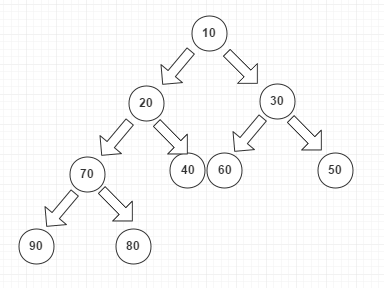
最大堆的例項

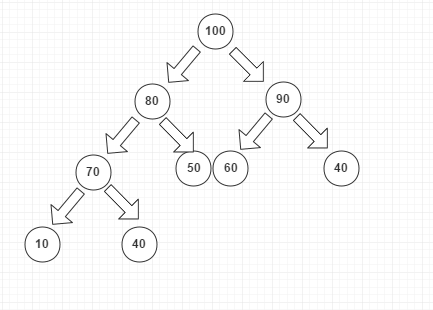
最小堆的例項

最大堆的刪除操作：

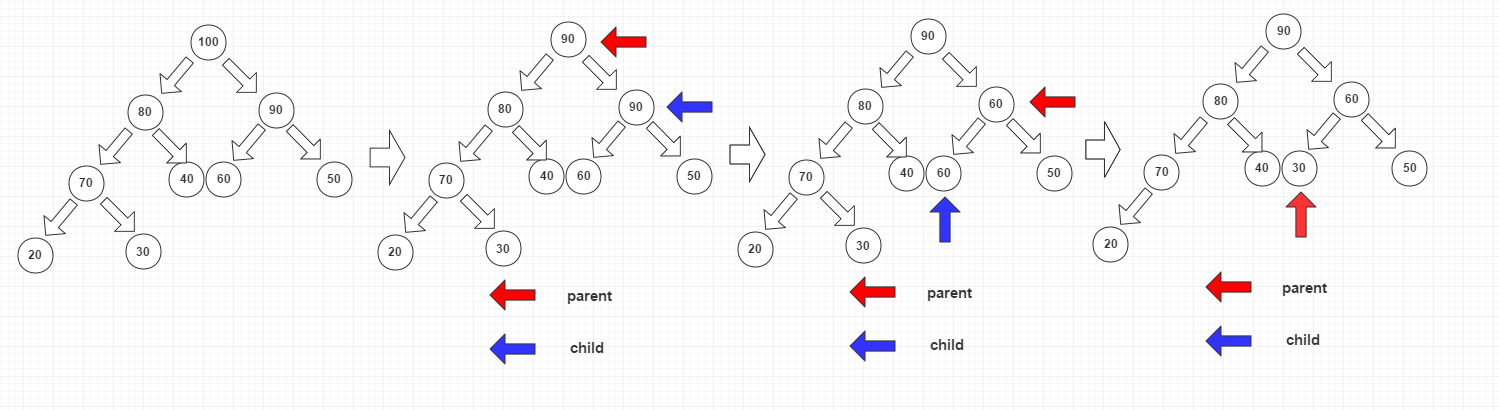
最大堆的刪除每次是從堆中刪除最大的元素，即堆頂
刪除的基本步驟：
1、堆的size減一，用變數儲存堆的末尾元素（本圖中是30）
2、刪除堆頂，並上浮兩個節點中的較大的子節點補位。
3、判斷child指向的節點是否越界，沒有的話，進入下一層，並重復第二步。
4、將末尾元素補位上浮到parent指向的節點。

最小堆的刪除操作：

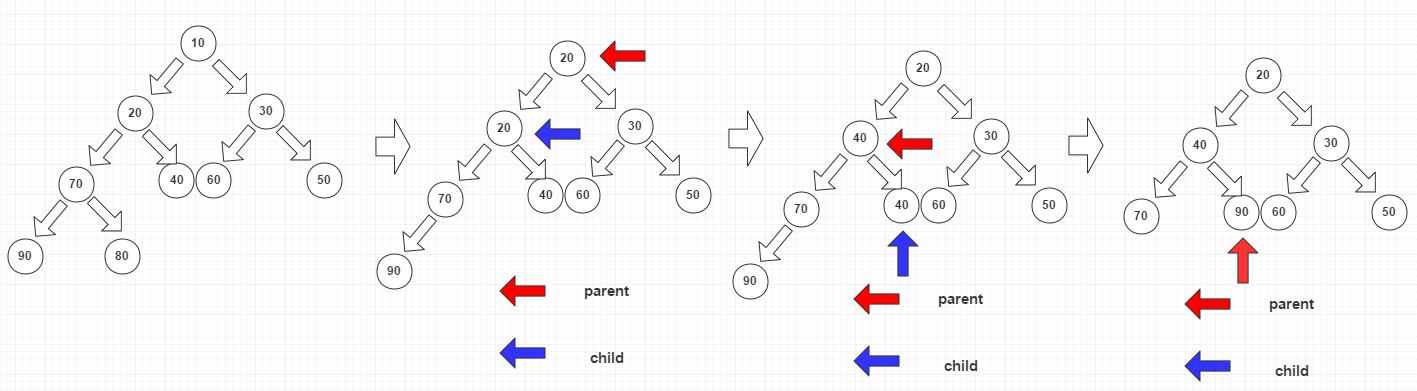
最大堆的刪除每次是從堆中刪除最小的元素，即堆頂
刪除的基本步驟：
1、堆的size減一，用變數儲存堆的末尾元素（本圖中是30）
2、刪除堆頂，並上浮兩個節點中的較小的子節點補位。
3、判斷child指向的節點是否越界，沒有的話，進入下一層，並重復第二步。
4、將末尾元素補位上浮到parent指向的節點。

最大堆的插入操作：

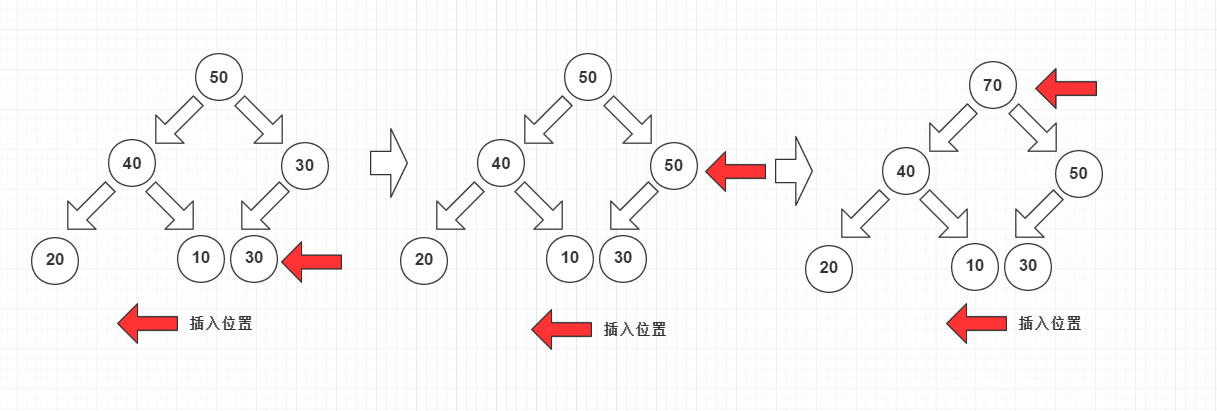
插入元素每次都從陣列末尾開始查詢查詢點：
1、若此時插入點不符合條件，則將插入點的父節點下沉。
2、判斷是否到頂（有哨兵在可以防住越界），沒有到頂繼續第一步。
3、找到插入點時插入。

最小堆的插入操作：

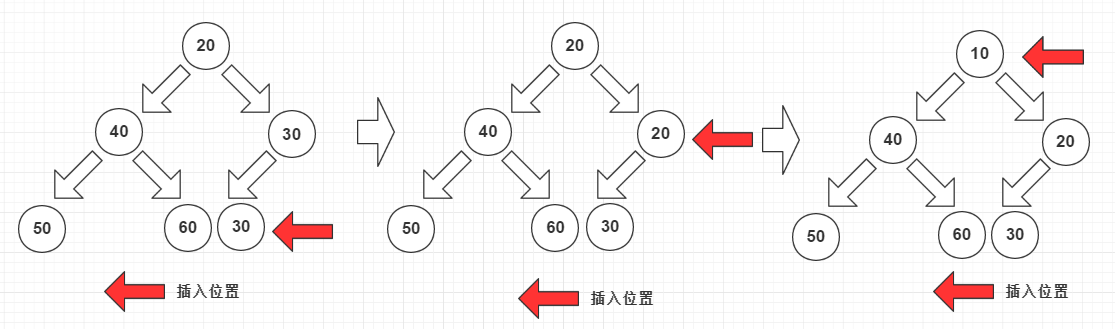
插入元素每次都從陣列末尾開始查詢查詢點：
1、若此時插入點不符合條件，則將插入點的父節點下沉。
2、判斷是否到頂（有哨兵在可以防住越界），沒有到頂繼續第一步。
3、找到插入點時插入。

具體的程式碼

/*
時間：2015.7.18
名稱：哈夫曼樹
操作：二叉堆的建立(建構函式)、最大最小堆的插入、最大最小堆的刪除、判斷堆空、判斷堆滿
簡述：
*/
#include<iostream>
using namespace std;
const int MAX_DATA=10000;//堆的可容納的最大元素，當做首位的哨兵用
const int MIN_DATA = -10000;//堆的可容納的最小元素，當做首位的哨兵用
enum Type{ Maximum, Minimum };//分別代表最大最小堆
class Heap
{
private:
    int *data;      //存放堆中元素
 

    int size;       //堆的目前大小
    int capacity;//堆的最大容量
    Type type;  //堆的具體型別
public:
    Heap()
    {
        int c, t;
        cout << "堆的最大容量為";
        cin >> c;
        cout << "堆的型別為(1為最大堆，0為最小堆):";
        cin >> t;
        size = c;//初始化是沒有元素
        capacity = MAX_DATA;//設定容量為最大
        if (t) type = Maximum;//設定堆的型別
        else type = Minimum;

        data = new int[capacity + 1];//動態申請記憶體
        if (type==Maximum) data[0] = MAX_DATA;//最大堆的0位置處放最大元素
        else data[0] = MIN_DATA;//最大堆的0位置處放最小元素

        //最大堆的元素輸入按照從大到小
        //最小堆的元素輸入按照從小到大
        for (int i = 1; i <= c; i++)
            cin >> data[i]; 
    };
    ~Heap()
    {
        delete[]data;
    };  

    //判斷堆是否滿
    int isFull()
    {
        if (size == capacity)
            return 1;
        else
            return 0;
    }

    //判斷堆是否空
    int isEmpty()
    {
        if (size == 0)
            return 1;
        else
            return 0;
    }

    //最大堆的插入
    void insertMaxHeap()
    {
        int i,item;
        cout << "輸入插入的元素";
        cin >> item;
        if (isFull())
        {
            cout << "堆已滿" << endl;
            return;
        }
        i = size + 1; size++;//先指向陣列的末尾，size增加1是因為插入時增加了一個元素    
        for (; data[i/2] < item; i /= 2)//找到第一個比item大的元素時結束
        {
            data[i] = data[i/2];//若沒有找到，則將上一層的元素挪到下一層
        }
        data[i] = item;//找到插入點，插入item
    }

    //最小堆的插入
    void insertMinHeap()
    {
        int i, item;
        cout << "輸入插入的元素";
        cin >> item;
        if (isFull())
        {
            cout << "堆已滿" << endl;
            return;
        }
        i = size + 1; size++;
        for (; data[i/2] > item; i /= 2)//找到第一個比item小的元素時結束
        {
            data[i] = data[i / 2];//沒有找到則將上一層元素挪到下一層
        }
        data[i] = item;//找到插入點，插入item
    }

    //最大堆的刪除
    int deleteMaxHeap()
    {
        //原理如下：記錄並刪除最大元素，然後自頂向下上浮其較大的子節點
        //上浮完畢後進入向下進入一層，最後將最小的元素補位上浮
        if (isEmpty())
        {
            size = 0;
            return MAX_DATA;//為空返回不可能的值
        }

        int child=1, parent=1;//指向父節點和子節點的遊標
        int max = data[1];//記錄最大值用於返回
        int last = data[size--];//記錄末尾最小值，並且size減1

        for (parent = 1; parent * 2 <= size; parent = child)//迴圈上浮子節點
        {
            child = parent * 2;//child指向其子節點
            if (child!=size)//有時只有一個子節點，這裡要防止越界
            if (data[child] < data[child + 1])//child指向的是較大的子節點
                child++;

            if (last<data[parent])//找到了min的插入點就代表上浮完畢，結束迴圈並插入
            if (last>data[child])
                break;
            else
                data[parent] = data[child];//沒有找到就繼續上浮
        }
        data[parent] = last;//將末尾的最小值補位上浮
        return max;
    }

    //最小堆的刪除
    int deleteMinHeap()
    {
        //原理如下：記錄並刪除最小元素，然後自頂向下上浮其較小的子節點
        //上浮完畢後進入向下進入一層，最後將最大的元素補位上浮
        if (isEmpty())
        {
            size = 0;
            return MIN_DATA;//為空返回不可能的值
        }
        int child=1, parent=1;//指向父節點和子節點的遊標
        int min = data[1];//記錄最小值用於返回
        int last= data[size--];//記錄末尾最後一個值

        for (parent=1; parent*2 <= size; parent = child)//迴圈上浮子節點
        {
            child = parent * 2;//child指向其子節點
            if (child!=size)
            if (data[child] > data[child + 1])//child指向的是較小的子節點
                ++child;

            if (last > data[parent])//找到了last的插入點就代表上浮完畢，結束迴圈並插入
            if (last < data[child])
                    break;
            else
                data[parent] = data[child];//沒有找到就繼續上浮
        }
        data[child] = last;//將末尾的最大值補位上浮
        return min;
    }

    //堆的檢視
    void show()
    {
        int change = 1,tota1 = 0;
        for (int i = 1; i <= size; i++)
        {
            if (change == i)
            {
                cout << endl;
                change *= 2;
            }
            cout << data[i] << ' ';
            tota1++;
        }
        cout << endl;
    }
};

int main()
{
    //主函式是測試程式碼
    Heap heap;
    heap.show();

    //heap.insertMaxHeap();
    heap.insertMinHeap();
    heap.show();

    //int i = heap.deleteMaxHeap();
    int i = heap.deleteMinHeap();
    heap.show();

    return 0;
}