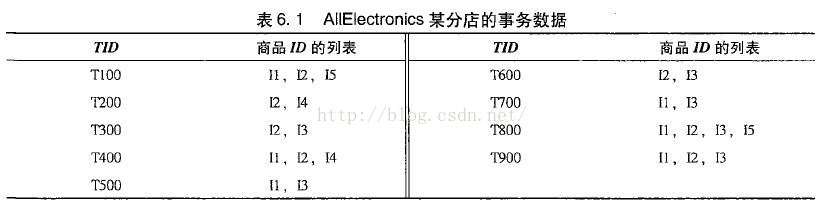
海量資料探勘MMDS week2: Association Rules關聯規則與頻繁項集挖掘
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記之association rules關聯規則與頻繁項集挖掘
{Frequent Itemsets: Often called "association rules," learn a number of techniques for finding items that appear unusually often together. The classical story of "beer and diapers" (people who buy diapers in a supermarket are unusually likely to buy beer) is an example of this data-mining technique.}
題外話: lz真的不建議看這個視訊,當你看了這個視訊後,你會發現,原本一個簡單的問題可以通過很優雅的方式簡單地解釋清楚的時候,主講人總是偏離方向,以一種相當繁瑣隱晦的形式講到另一個地方去,而讓人一下子就可以明白的解釋總是講不出來,讓人看不懂(說真的,那個比較老的主講人講解的是相當水),並且製作的ppt中的語句完全不是最好的,總是缺點什麼,總要加一點註釋在下面才能更好明白那是什麼意思。所以關於頻繁項集挖掘以及關聯規則,lz建議看看《資料探勘概念與技術》這本書中第六章 挖掘頻繁模式、關聯和相關性:基本概念與方法的內容,講的相當清晰易懂)
Frequent Itemsets頻繁項集
與相似性分析的區別:相似性分析,研究的物件是集合之間的相似性關係。而頻繁項集分析,研究的集合間重複性高的元素子集。
Market-Basket 模型及其應用
Note: 一個item可以看成是買的一個東西,其集合就是項集。一個basket就是買的東西的集合,也是一個項集,但一般看作是多個項集的集合。
頻繁項集的應用:真實超市購物籃的分析,文件或網頁的關聯程式分析,文件的抄襲分析,生物標誌物(疾病與某人生物生理資訊的關係)
應用一:人們會同時買什麼
Note:
1. Run a sale on diapers; raise price of beer.是一種營銷策略,但是反過來卻不是。這就要分析頻繁項集的原因。
2. 當然這種營銷策略只對實體店有效。超市購物籃的分析,主要是針對實體銷售商,而不是線上零售商,這是因為實體銷售可以找點頻繁項集合後,可以採取對一種頻繁項商品促銷,而擡高相關的頻繁項其他商品的價格來獲利,因為客戶一般不會去另外一家店購買其他的商品。而這種策略在線上銷售時,會忽略“長尾”客戶的需求。對於實體銷售,商品的數量和空間資源有限,所以只能針對一些暢銷商品進行關注和指定策略。而對於線上銷售,沒有資源限制,而且客戶切換商戶很方便,所以實體店銷售的策略不合適線上銷售,線上銷售更應該關注相似客戶群的分析,雖然他們的購買的產品不是最暢銷、頻繁的,但對客戶群的偏好分析,可以很容易做到對每個客戶進行定製化廣告推薦,所以,相似性分析對線上銷售更為重要。
應用二:抄襲plagiarism檢測
Note: the basket corresponding to a sentence contains all the documents in which that sentence appears.
應用三:詞關聯
關聯規則Association Rules、支援度與置信度
Support支援度

支援度: 包含頻繁項集F的集合的數目。項集的支援度就是項集應該在所有basket中出現的數目。>=項集的支援度的項集都是頻繁項集。
Confidence置信度

置信度:confidence(A=>B) = P(B|A) = support(A U B)/support(A) = support_count(A U B)/support_count(A),就是itemA存在時itemB也存在的條件概率,也是頻繁項A與某項B的並集的支援度 與 頻繁項集A的支援度的比值。
尋找關聯規則和頻繁項集
關聯規則挖掘兩個步驟
1. 尋找所有頻繁項集(滿足最小支援度的項集)
2. 由頻繁項集產生關聯規則(滿足最小支援度和最小可信度的項集)
Note: 確定頻繁項集,{i}只需要support,而{i,j}則需要support*confidence.
Note:
1. 這種尋找關聯規則的方法步驟是:先找到支援度>=cs的,然後去掉其中一個item j,找到支援度>=s的,這樣去掉j後的項集{i}->j的置信度>=c,{i}->j就是一個關聯規則。
2. 這種解釋完全沒有《資料探勘概念與技術》中的解釋清晰明瞭。
頻繁項集的計算模型
演算法瓶頸
尋找頻繁二項集的演算法
Naive Algorithm樸素演算法
頻繁項對{i, j}在記憶體中的存放方式
{用什麼資料結構來儲存頻繁二項集數對更有效}

Triangular Matrix三角陣方法
{採用一個數組來儲存這個三角陣中的元素,它可以節省二維陣列一半的空間}
Note: translate from an items name in the data to its integer.A hash table whose key is the original name of the item in the data will do just fine.
Note: 因為pairs存放在一個一維陣列中。則頻繁對(i, j)存放的位置就是上面這個公式。
Tabular三元組方法
{當頻繁項對的數目小於C(n, 2)的數目的1/3時,三元組的方式相對於三角陣比較有優勢}
Note: 連結串列實現需要指標指向下一個,這樣就是16p而不是12p了。
兩種方法的比較和取捨
如果有大於1/3的候選二項集是頻繁二項集,那麼使用Triangular結構儲存比較好。if more than one-third of possible pairs are present in at least one basket,you prefer the triangular matrix.
設頻繁一項集數目為N,頻繁二項集的數目為M,候選二項集自然就是N^2/2。則使用Triangular矩陣儲存頻繁二項集的空間為4*N^2/2, 使用Tabular結構儲存頻繁二項集的空間為12*M。當大於1/3的候選二項集是頻繁二項集,也就是1/3 * N^2/2 < M,這時4*N^2/2 < 12*M,使用Triangular矩陣儲存頻繁二項集的空間較小。
A-priori演算法
{通過限制候選產生來發現頻繁項集。Aprior有點類似廣度優先的演算法。}
頻繁項集的先驗性質:單調性和反單調性
Note: 尋找頻繁二項集是掃描兩次,頻繁k項集當然是k次。if you want to go pass pairs to larger item sets,then you need k passes, define frequent items that's of size up to K.
A-priori演算法步驟
頻繁二項集的挖掘

If there's still too many counts to maintain in main memory,we need to try something else,a different algorithm,splitting the task among different processors, or even buying more memory.
A-Priori演算法中使用Triangular Matrix

Note:
1. 也就是第一次掃描後,選出頻繁一項集並重新編號,組成Triangular Matrix。在Triangular Matrix中再選出頻繁二項集重新編號,並組成Triangular Matrix,再進行下一次Apriori演算法的計算。
2. There are better ways to organize the table that save space,if the fraction of items that are frequent is small.For example, we could use a hash table in which we stored only the frequent items with the key being the old number and the associated value being the new number.(也就是Tabular?)
頻繁K項集挖掘

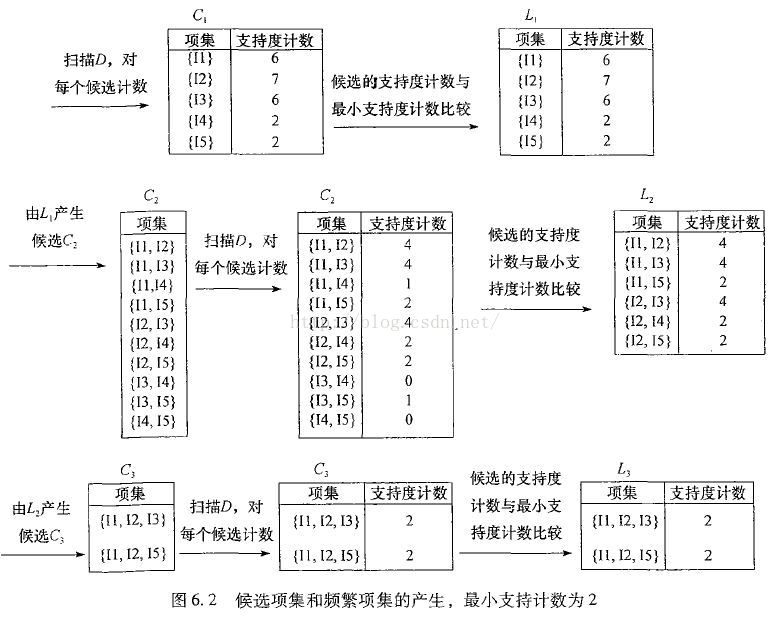
資料探勘概念與技術中對Apriori演算法的圖解
是不是簡單清晰得多!
Apriori演算法記憶體需求分析
每次計算一個頻繁k{k = 1-K}項集,都要掃描一次basket(transaction交易)
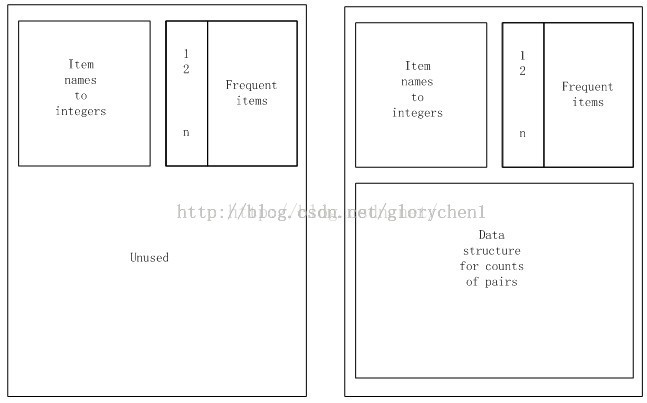
Apriori演算法的記憶體的使用情況,左邊為第一步時的記憶體情況,右圖為第二步時記憶體的使用情況
在第一步(對所有item掃描計數,並選出頻繁一項集)裡,我們只需要兩個表,一個用來儲存項的名字到一個整數的對映,用這些整數值代表項,一個數組來計數這些整數。
Reviews複習
Triangular Matrix和Tabular的選擇
Note: S是N和M的函式。
從上面分析可知:如果有大於1/3的候選二項集是頻繁二項集(也就是1/3 * N^2/2 < M <=> N^2 < 6M),那麼使用Triangular結構儲存比較好。並且使用Triangular矩陣儲存頻繁二項集的空間為4*N^2/2, 使用Tabular結構儲存頻繁二項集的空間為12*M。
N = 10,000, M=50,000,000,則N^2 = 10^8 < 6M=3*10^8,故使用Triangular矩陣來儲存頻繁二項集,空間為S = 4*N^2/2=2*10^8。(的確比12*M = 6*10^8小)
N = 100,000, M=40,000,000,則N^2 = 10^10 > 6M=2.4*10^8,故使用Tabular來儲存頻繁二項集,空間為S =12*M=4.8*10^8。(的確比4*N^2/2= 2*10^10小)
N = 100,000, M=100,000,000,則N^2 = 10^10 > 6M=6*10^8,故使用Tabular矩陣來儲存頻繁二項集,空間為S =12*M=12*10^8。(的確比4*N^2/2= 2*10^10小)
N = 30,000, M=100,000,000,則N^2 = 9*10^8 > 6M=6*10^8,故使用Tabular矩陣來儲存頻繁二項集,空間為S =12*M=18*10^8。(的確比4*N^2/2= 12*10^8小)
相關推薦
海量資料探勘MMDS week2: Association Rules關聯規則與頻繁項集挖掘
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記之association rules關聯規則與頻繁項集挖掘 {Frequent Itemsets: Often called "associatio
海量資料探勘MMDS week2: 頻繁項集挖掘 Apriori演算法的改進:基於hash的方法
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記之關聯規則Apriori演算法的改進:基於hash的方法:PCY演算法, Multistage演算法, Multihash演算法 Apriori演
海量資料探勘MMDS week2: 頻繁項集挖掘 Apriori演算法的改進:非hash方法
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記之關聯規則Apriori演算法的改進:非hash方法 - 大資料集下的頻繁項集:挖掘隨機取樣演算法、SON演算法、Toivonen演算法 Apri
資料探勘中的模式發現(一)頻繁項集、頻繁閉項集、最大頻繁項集
Frequent Itemset(頻繁項集) 稱I={i1,i2,...,im}I=\{i_1, i_2, ..., i_m\}I={i1,i2,...,im}為項(Item)的集合,D={T1,T2,...,Tn}D=\{T_1, T_2, ...,T_
海量資料探勘MMDS week4: 推薦系統之資料降維Dimensionality Reduction
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記 推薦系統Recommendation System之降維Dimensionality Reduction{部落格內容:推薦系統有一種推薦稱作隱語義模型
HAWQ + MADlib 玩轉資料探勘之(七)——關聯規則方法之Apriori演算法
一、關聯規則簡介 關聯規則挖掘的目標是發現數據項集之間的關聯關係,是資料挖據中一個重要的課題。關聯規則最初是針對購物籃分析(Market Basket Analysis)問題提出的。假設超市經理想更多地瞭解顧客的購物習慣,特別是想知道,哪些商品顧客可能會在一次購
DataMining學習1_資料探勘技術(三)——關聯分析
3、關聯分析 3.1、基本概念 (1)通常認為項在事物中出現比不出現更重要,因此項是非對稱二元變數。(2)關聯規則是形如X->Y的蘊涵表示式,其中X和Y是不相交的項集,即X交Y=空。(3)由關聯規則作出的推論並不必然蘊涵因果關係。它只表示規則前件和後件中的項明
資料探勘十大經典演算法--CART: 分類與迴歸樹
一、決策樹的型別 在資料探勘中,決策樹主要有兩種型別: 分類樹 的輸出是樣本的類標。 迴歸樹 的輸出是一個實數 (例如房子的價格,病人呆在醫院的時間等)。 術語分類和迴歸樹 (CART) 包含了上述兩種決策樹, 最先由Breiman 等提出.分類樹和迴歸樹有些共同點和不同
資料探勘—LDA,PCA特徵提取降維與SVM多分類在人臉識別中的應用-資料集ORL
@vision 3 @author:馬旭 @tel:13952522076 @email:[email protected] 執行:執行predict.m檔案; 結果:時間一般為0.2秒左右,正確率100%;(因為測試集比較少) 預處理資料preprocess
程式設計師面試、演算法研究、程式設計藝術、紅黑樹、資料探勘5大經典原創系列集錦與總結
作者:July--結構之法演算法之道blog之博主。 時間:2010年10月-2012年9月 (一直在收錄本blog最新updated文章)。 出處:http://blog.csdn.net/v_JULY_v 。 宣告:版權所有,侵犯必究。 前言 開博已過20個
資料探勘---頻繁項集挖掘Apriori演算法的C++實現
1 準備 2 作業粗糙翻譯內容 2.1 前言 程式設計作業可能比書面作業花費更多的時間,而這也算是你最後成績的10%,所以請提前開始; 這是個人作業,你可以與你的同學或者老師交流,但是不能夠共享程式碼和抄襲; 類似的庫或頻繁模式挖掘演算
資料探勘演算法之-關聯規則挖掘(Association Rule)
在資料探勘的知識模式中,關聯規則模式是比較重要的一種。關聯規則的概念由Agrawal、Imielinski、Swami 提出,是資料中一種簡單但很實用的規則。關聯規則模式屬於描述型模式,發現關聯規則的演算法屬於無監督學習的方法。 一、關聯規則的定義和屬性 考察一
資料探勘、資料分析、海量資料處理的面試題(總結july的部落格)
緣由 由於有面試通知,現在複習一下十道和海量資料處理相關的題。兩篇部落格已經講的非常完備了,但是我怕讀懂了並非真的懂,所以必須自己複述一遍。 面試歸類 下面6個方面覆蓋了大多數關於海量資料處理的面試題: 分而治之/hash對映 + hash統計 + 堆/快速/歸併排序
資料探勘領域中的分類和迴歸區別是什麼?
先簡單的說下吧,下面給出實際例子 類和迴歸的區別在於輸出變數的型別。定量輸出稱為迴歸,或者說是連續變數預測;定性輸出稱為分類,或者說是離散變數預測。舉個例子:預測明天的氣溫是多少度,這是一個迴歸任務;預測明天是陰、晴還是雨,就是一個分類任務。 拿支援向量機舉個例子,分類問題
大資料就業前景怎麼樣?hadoop工程師、資料探勘、資料分析師薪資多少?
近幾年來,大資料這個詞突然變得很火,不僅納入阿里巴巴、谷歌等網際網路公司的戰略規劃中,同時也在我國國務院和其他國家的政府報告中多次提及,大資料無疑成為當今網際網路世界中的新寵兒。 《大資料人才報告》顯示,目前全國的大資料人才僅46萬,未來3-5年內大資料人才的缺口將高達150萬,越來越多
利用Python學習資料探勘【0】
相信看到這篇文章的你一定是對資料分析,資料探勘有興趣,或者想從事和方面。本文不再累述python對資料分析的重要,資料分析這門的由來之類的。 在這裡,我單刀直入,已我學習資料探勘3年來的經歷告訴大家怎麼去學,以讓大家少走彎路。純個人見解,如有不對,還請各位留言指教。 話不多說,直接放圖。
利用Python學習資料探勘【2】
本文結合程式碼例項待你上手python資料探勘和機器學習技術。 本文包含了五個知識點: 1. 資料探勘與機器學習技術簡介 2. Python資料預處理實戰 3. 常見分類演算法介紹
利用 Python學習資料探勘【1】
覆蓋使用Python進行資料探勘查詢和描述資料結構模式的實踐工具。 第一節 介紹 資料探勘是一個隱式提取以前未知的潛在有用的資料資訊提取方式。它使用廣泛,並且是眾多應用的技術基礎。 本文介紹那些使用Python資料探勘實踐用於發現和描述結構模式資料的工具。近些年來,Python在
《資料探勘核心技術揭祕》筆記
原先我對於資料探勘只停留在了爬蟲獲取資料,使用工具對資料進行清洗,然後整理彙總出需要的資訊的這個層次。看完這本書之後才發現了之前使用爬蟲得到資料只能叫做資料獲取,真正的資料探勘遠遠複雜,在資料探勘中有著那麼多的magic的演算法,其中每個單元的知識都需要一本書去好好學習,這裡只是簡單的介
python 資料分析 資料探勘 人工智慧 教程
python 資料分析 資料探勘 人工智慧 教程 python 資料分析 資料探勘 人工智慧 教程 資料分析 pyhon程式碼 資料分析英文教程 上百g資料,用於資料分析,大資料 新聞資料 產業資料 谷歌資料 維基百科等等 資料 統一解壓密碼 qq92313271