相關背景

• NN的簡單含義
  簡單地說，最近鄰檢索就是根據資料的相似性，從資料庫中尋找與目標資料最相似的專案，而這種相似性通常會被量化到空間上資料之間的距離，可以認為資料在空間中的距離越近，則資料之間的相似性越高。當需要查詢離目標資料最近的前k個數據項時，就是k最近鄰檢索（K-NN)。

• 最近鄰檢索的應用領域
  在當今這個移動網際網路時代，我們的日常生活每天都面臨著海量資料地衝擊，諸如像個人資訊、視訊
  記錄、影象採集、地理資訊、日誌文件等，面對如此龐大且日益增長的資料資訊，如何對我們需要的資訊有效的儲存及索引與查詢是目前國內外研究的熱點。
  最近鄰檢索起初作為具有查詢相似性文件資訊的方法被應用於文件檢索系統，隨後在地理資訊系統中，最近鄰檢索也被廣泛應用於位置資訊，空間資料關係的查詢、分析與統計，如今在影象檢索、資料壓縮、模式識別以及機器學習等領域都有非常重要的作用，而在這些領域中大多會涉及到海量的多媒體資料資訊的處理，其中包括大量影象、視訊資訊。在影象處理與檢索的研究中，基於內容的影象檢索方法（CBIR）是目前的主流，這裡的“內容”指的是影象中包含的主要物件的幾何形狀、顏色強度、表面紋理等外在特性，以及前景與後景的對比程度等整體特徵。為了獲得影象中這些特定的資訊或方便後續處理，我們通常會利用多種不同的描述方式來表示影象，包括區域性特徵描述子（SIFT、SURF、BRIEF） ，全域性特徵描述子（GIST），特徵頻率直方圖，紋理資訊，顯著性區域等。最近鄰檢索的引入將影象檢索轉化到特徵向量空間，通過查詢與目標特徵向量距離最近的向量來獲得相應影象之間的關係。這種特徵向量之間的距離通常被定義為歐幾里得距離（Euclidean distance)，即是空間中兩點之間的直線距離。

最近鄰檢索的發展

最近鄰檢索作為資料檢索中使用最為廣泛的技術一直以來都是國內外學者研究的熱點。在近些年的研究中湧現出大量以最近鄰檢索或近似最近鄰檢索為基本思想的方法，其中一類是基於提升檢索結構效能的方法，主要方法大多基於樹形結構。另一類主要基於對資料本身的處理，包括雜湊演算法、向量量化方法等。

• 精確檢索
  精確檢索中資料維度一般較低。所以會採用簡單的蠻力方法，也就是平常所說的窮舉搜尋，在資料庫中依次計算其中樣本與所查詢資料之間的距離，抽取出所計算出來的距離最小的樣本即為所要查詢的最近鄰。這樣做的缺點是當資料量非常大的時候，搜尋效率急劇下降。因為實際資料會呈現出簇狀的聚類形態，所以可以考慮對資料庫中的樣本資料構建資料索引，索引樹就是最常見的方法。其基本思想是對搜尋空間進行層次劃分，再進行快速匹配。比如當d=1時，只要採用傳統的二分查詢法或者各類平衡樹就能找到最近鄰；當d=2時，情況稍稍複雜點，一般則將最近鄰檢索問題轉化為求解查詢點究竟落在哪個區域的Voronoi圖問題，再通過二分查詢樹就能很好的解決，空間複雜度和查詢複雜度分別為0(n)，O(log n)。當資料維度不太高（如d< 20)，通常採用樹型索引結構對資料進行分割槽以實現高效索引，如最經典的KD樹演算法 、R樹、M樹等等，它們的時間和空間複雜度都是以d為指數的指數級別的，在實際搜尋時也取得了良好的效果。
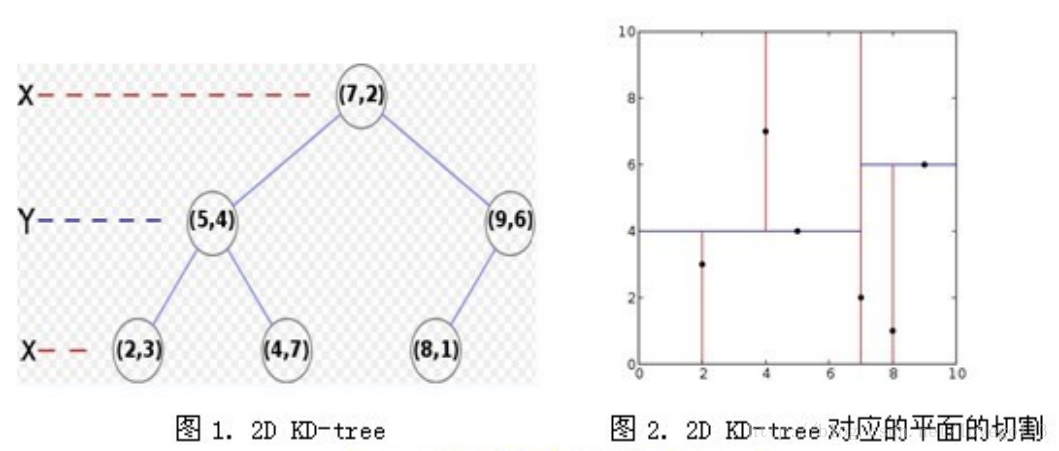
  KD-Tree 是由 Finkel 和 Bentley 共同設計提出的對二叉搜尋樹的推廣，利用KD-Tree 我們可以對一個由 K 維資料組成的資料集合進行劃分，劃分時在樹的每一層上根據設定好的分辨器（discriminator）選取資料的某一維，比較待分配資料與節點資料在這一維度上數值的大小，根據結果將資料劃分到左右子樹中。比如X= {（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}這樣的一個由6個點構成的二維點集，我們首先對它的第一維X進行劃分，根據二分將（7,2）作為根節點，那麼資料點的x軸小於7的劃分到左子樹，大於7的劃分到右子樹；再對第二維Y進行劃分時，則根據資料點的y軸的大小進行左右劃分。
  
  
  那麼對於k維的點集，我們只需要依照上面的方法進行k層這樣的劃分就可以構成一棵KD-Tree 。然而在做最近鄰檢索時雖然從根節點到葉子節點自上而下的檢索較線性查詢節省了時間，但為了找到“最近鄰”還需要進行回溯查詢比較那些不在已訪問分支中的節點，所以當 K 很大即資料維度很高時演算法複雜度將大大提高。
• 近似檢索
  面對龐大的資料量以及資料庫中高維的資料資訊，現有的基於 NN 的檢索方法無法獲得理想的檢索效果與可接受的檢索時間。進而有研究人員開始關注近似最近鄰檢索（Approximate Nearest Neighbor，ANN），近似最近鄰檢索利用了資料量增大後資料之間會形成簇狀聚集分佈的特性，通過對資料分析聚類的方法對資料庫中的資料進行分類或編碼，對於目標資料根據其資料特徵預測其所屬的資料類別，返回類別中的部分或全部作為檢索結果。近似最近鄰檢索的核心思想是搜尋可能是近鄰的資料項而不再只侷限於返回最可能的專案，在犧牲可接受範圍內的精度的情況下提高檢索效率。主要分為兩種辦法，一種是採用雜湊雜湊的辦法，另一種則是向量量化。
  區域性敏感雜湊（LSH）最早由 P. Indyk and R. Motwani 提出，其核心思想是：在高維空間相鄰的資料經過雜湊函式的對映投影轉化到低維空間後，他們落入同一個吊桶的概率很大而不相鄰的資料對映到同一個吊桶的概率則很小。在檢索時將歐式空間的距離計算轉化到漢明（Hamming）空間，並將全域性檢索轉化為對對映到同一個吊桶中的資料進行檢索，從而提高了檢索速度。這種方法的主要難點在於如何尋找適合的雜湊函式，它的雜湊函式必須滿足以下兩個條件：
  1）如果d(x,y) ≤ d1， 則h(x) = h(y)的概率至少為p1；
  2）如果d(x,y) ≥ d2， 則h(x) = h(y)的概率至多為p2；
  其中d(x,y)表示x和y之間的距離，d1 < d2， h(x)和h(y)分別表示對x和y進行hash變換。後續的研究中有許多尋找雜湊函式的方法。
  
  
  向量量化的代表就是乘積量化（PQ），PQ的主要思想是將特徵向量進行正交分解，在分解後的低維正交子空間上進行量化，由於低維空間可以採用較小的碼本進行編碼，因此可以降低資料儲存空間 。PQ方法採用基於查詢表的非對稱距離計算(Asymmetric Distance Computation，ADC)快速求取特徵向量之間的距離，在壓縮比相同的情況下，與採用漢明距離的二值編碼方法，採用ADC的PQ方法的檢索精度更高。然而，PQ方法假設各子空間的資料分佈相互獨立，當子空間資料的相互依賴較強時檢索精度下降
  嚴重。針對這點就有通過旋轉矩陣來調整資料空間的OPQ（Optimized Product Quantization）演算法，如下圖，原本按照1234維排列的資料空間通過與正交矩陣R相乘，其維度排列變成了3214，那麼我們就可以尋找一個合適的正交矩陣重新排列向量的維度，使得其劃分的各子空間之間的依賴性達到最小。
  
  另外還有一個AQ（Additive Quantization）演算法，它與PQ演算法一樣，也是將d維向量劃分為m個子向量，對應m個碼本，每個碼本包含k個碼字，然而，PQ中碼字長度為d／m，而AQ 中碼字長度為d，與待編碼特徵向量長度一致。
  

注：文中部分例圖來自於網路和相關文章。
展望：以後的資料基本都是大資料量且高維度的，另外雜湊雜湊方法基於二進位制編碼的近似最近鄰查詢雖然大大提高了檢索效率，但其檢索的準確度始終不高，因此以乘積量化為代表的向量量化方法可能將是一個可行的辦法。