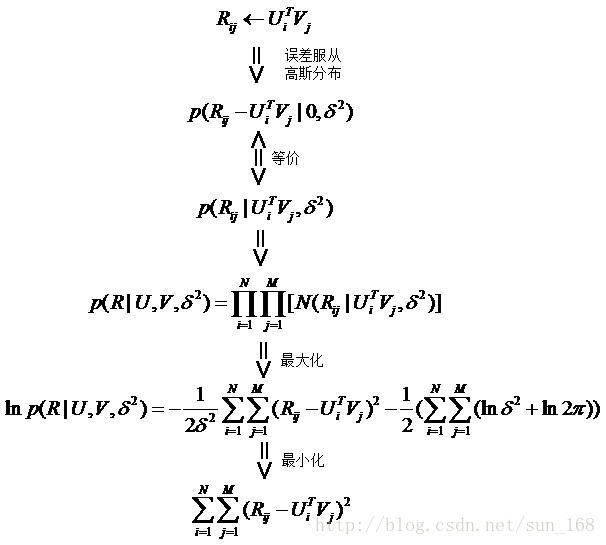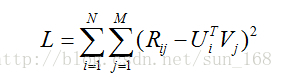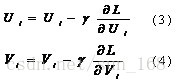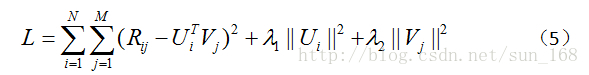資料探勘基礎知識-矩陣(分解)
1. 矩陣知識:
//特徵值,行列式,秩,對稱矩陣,單位矩陣,正定半正定,雅可比等等!!
正交矩陣:
如果:AA'=E(E為單位矩陣,A'表示“矩陣A的轉置矩陣”。)或A′A=E,則n階實矩陣A稱為正交矩陣, 若A為正交陣,則滿足以下條件: 1) AT是正交矩陣 2)(E為單位矩陣) 3) A的各行是單位向量且兩兩正交 4) A的各列是單位向量且兩兩正交 5) (Ax,Ay)=(x,y) x,y∈R 6) |A| = 1或-1 2. 矩陣分解(推薦系統)基本思想: 矩陣分解的思想簡單來說就是每一個使用者和每一個物品都會有自己的一些特性,用矩陣分解的方法可以從評分矩陣中分解出使用者——特性矩陣,特性——物品矩陣,這樣做的好處一是得到了使用者的偏好和每件物品的特性,二是見底了矩陣的維度。圖示如下: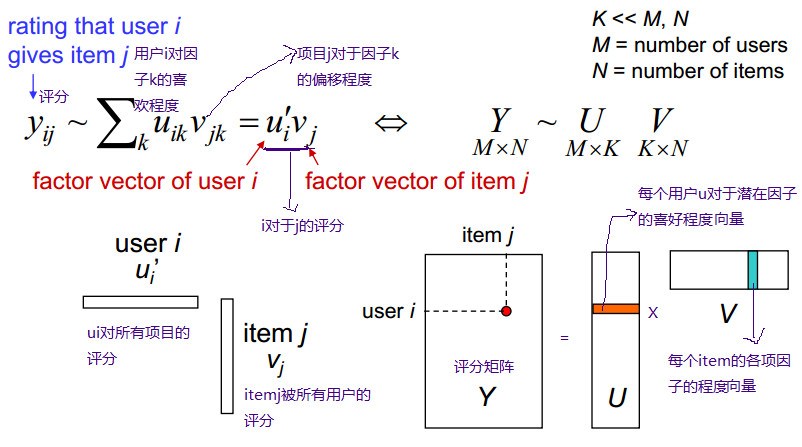
用使用者對電影來舉例子就是:每個使用者看電影的時候都有偏好,這些偏好可以直觀理解成:恐怖,喜劇,動作,愛情等。使用者——特性矩陣表示的就是使用者對這些因素的喜歡程度。同樣,每一部電影也可以用這些因素描述,因此特性——物品矩陣表示的就是每一部電影這些因素的含量,也就是電影的型別。這樣子兩個矩陣相乘就會得到使用者對這個電影的喜歡程度。 ---------------------------------------------------------------------------------------------------------------------------
SVD分解:
假設M是一個m×n階矩陣,其中的元素全部屬於域 K,也就是 實數域或複數域。如此則存在一個分解使得 M = UΣV*, 其中U是m×m階酉矩陣;Σ是半正定m×n階對角矩陣;而V*,即V的共軛轉置,是n×n階酉矩陣。這樣的分解就稱作M的奇異值分解。Σ對角線上的元素Σi,i即為M的奇異值。 在矩陣M的奇異值分解中 M = UΣV* ·U的列(columns)組成一套對M的正交"輸入"或"分析"的基向量。這些向量是MM*的特徵向量。 ·V的列(columns)組成一套對M的正交"輸出"的基向量。這些向量是M*M的特徵向量。 ·Σ對角線上的元素是奇異值,可視為是在輸入與輸出間進行的標量的"膨脹控制"。這些是M*M及MM*的奇異值,並與U和V的行向量相對應matlab code:
>> A
A =
1 2 3 4 5
4 3 2 1 4
>> [u,s,v] = svd(A);
>> u
u =
-0.7456 -0.6664
-0.6664 0.7456
>> s
s =
9.5264 0 0 0 0
0 3.2012 0 0 0
>> v
v =
-0.3581 0.7235 -0.2591 -0.1658 -0.5038
-0.3664 0.2824 0.2663 0.8031 0.2647
-0.3747 -0.1587 0.8170 -0.2919 -0.2858
-0.3830 -0.5998 -0.3560 0.3230 -0.5123
-0.6711 -0.1092 -0.2602 -0.3714 0.5762
-------------------------------------------------------------------------------------
直觀地說:
假設我們有一個矩陣,該矩陣每一列代表一個user,每一行代表一個item。

如上圖,ben,tom....代表user,season n代表item。
矩陣值代表評分(0代表未評分):
如 ben對season1評分為5,tom對season1 評分為5,tom對season2未評分。
機器學習和資訊檢索:
機器學習的一個最根本也是最有趣的特性是資料壓縮概念的相關性。
如果我們能夠從資料中抽取某些有意義的感念,則我們能用更少的位元位來表述這個資料。
從資訊理論的角度則是資料之間存在相關性,則有可壓縮性。
SVD就是用來將一個大的矩陣以降低維數的方式進行有損地壓縮。
降維:
下面我們將用一個具體的例子展示svd的具體過程。
首先是A矩陣。
A =
5 5 0 5
5 0 3 4
3 4 0 3
0 0 5 3
5 4 4 5
5 4 5 5
(代表上圖的評分矩陣)
使用matlab呼叫svd函式:
[U,S,Vtranspose]=svd(A)
U =
-0.4472 -0.5373 -0.0064 -0.5037 -0.3857 -0.3298
-0.3586 0.2461 0.8622 -0.1458 0.0780 0.2002
-0.2925 -0.4033 -0.2275 -0.1038 0.4360 0.7065
-0.2078 0.6700 -0.3951 -0.5888 0.0260 0.0667
-0.5099 0.0597 -0.1097 0.2869 0.5946 -0.5371
-0.5316 0.1887 -0.1914 0.5341 -0.5485 0.2429
S =
17.7139 0 0 0
0 6.3917 0 0
0 0 3.0980 0
0 0 0 1.3290
0 0 0 0
0 0 0 0
Vtranspose =
-0.5710 -0.2228 0.6749 0.4109
-0.4275 -0.5172 -0.6929 0.2637
-0.3846 0.8246 -0.2532 0.3286
-0.5859 0.0532 0.0140 -0.8085
分解矩陣之後我們首先需要明白S的意義。
可以看到S很特別,是個對角線矩陣。
每個元素非負,而且依次減小,具體要講明白元素值的意思大概和線性代數的特徵向量,特徵值有關。
但是可以大致理解如下:
線上性空間裡,每個向量代表一個方向。
所以特徵值是代表該矩陣向著該特徵值對應的特徵向量的方向的變化權重。
所以可以取S對角線上前k個元素。
當k=2時候即將S(6*4)降維成S(2*2),
同時U(6*6),Vtranspose(4*4)相應地變為 U(6*2),Vtranspose(4*2).
如下圖(圖片裡的usv矩陣元素值和我自己matlab算出的usv矩陣元素值有些正負不一致,但是本質是相同的):

此時我們用降維後的U,S,V來相乘得到A2
A2=U(1:6,1:2)*S(1:2,1:2)*(V(1:4,1:2))' //matlab語句
A2 =
5.2885 5.1627 0.2149 4.4591
3.2768 1.9021 3.7400 3.8058
3.5324 3.5479 -0.1332 2.8984
1.1475 -0.6417 4.9472 2.3846
5.0727 3.6640 3.7887 5.3130
5.1086 3.4019 4.6166 5.5822
此時我們可以很直觀地看出,A2和A很接近,這就是之前說的降維可以看成一種資料的有失真壓縮。
接下來我們開始分析該矩陣中資料的相關性。
我們將u的第一列當成x值,第二列當成y值。即u的每一行用一個二維向量表示,同理v的每一行也用一個二維向量表示。
如下圖:

從圖中可以看出:
Season5,Season6特別靠近。Ben和Fred也特別靠近。
同時我們仔細看一下A矩陣可以發現,A矩陣的第5行向量和第6行向量特別相似,Ben所在的列向量和Fred所在的列向量也特別相似。
所以從直觀上我們發現U矩陣和V矩陣可以近似來代表A矩陣,換據話說就是將A矩陣壓縮成U矩陣和V矩陣,至於壓縮比例得看當時對S矩陣取前k個數的k值是多少。
到這裡,我們已經完成了一半。
尋找相似使用者:
依然用例項來說明:
我們假設,現在有個名字叫Bob的新使用者,並且已知這個使用者對season n的評分向量為:[5 5 0 0 0 5]。(此向量為列向量)
我們的任務是要對他做出個性化的推薦。
我們的思路首先是利用新使用者的評分向量找出該使用者的相似使用者。

如上圖(圖中第二行式子有錯誤,Bob的轉置應為行向量)。
對圖中公式不做證明,只需要知道結論,結論是得到一個Bob的二維向量,即知道Bob的座標。
將Bob座標新增進原來的圖中:

然後從圖中找出和Bob最相似的使用者。
注意,最相似並不是距離最近的使用者,這裡的相似用餘弦相似度計算。(關於相似度還有很多種計算方法,各有優缺點)
即夾角與Bob最小的使用者座標。
可以計算出最相似的使用者是ben。
接下來的推薦策略就完全取決於個人選擇了。
這裡介紹一個非常簡單的推薦策略:
找出最相似的使用者,即ben。
觀察ben的評分向量為:【5 5 3 0 5 5】。
對比Bob的評分向量:【5 5 0 0 0 5】。
然後找出ben評分過而Bob未評分的item並排序,即【season 5:5,season 3:5】。
即推薦給Bob的item依次為 season5 和 season3。
最後還有一些關於整個推薦思路的可改進的地方:
1.
svd本身就是時間複雜度高的計算過程,如果資料量大的情況恐怕時間消耗無法忍受。
不過可以使用梯度下降等機器學習的相關方法來進行近似計算,以減少時間消耗。
2.
相似度計算方法的選擇,有多種相似度計算方法,每種都有對應優缺點,對針對不同場景使用最適合的相似度計算方法。
3.
推薦策略:首先是相似使用者可以多個,每個由相似度作為權重來共同影響推薦的item的評分。
-----------------------------------------------------------------------------------------------------------------------------------------------------
3. FMF 概率矩陣分解:
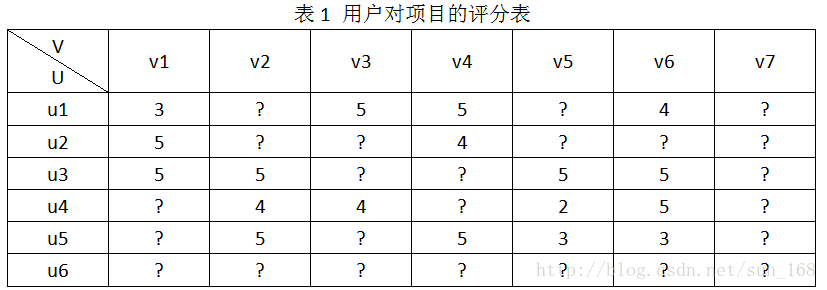
為了方便介紹,假設推薦系統中有使用者集合有6個使用者,即U={u1,u2,u3,u4,u5,u6},專案(物品)集合有7個專案,即V={v1,v2,v3,v4,v5,v6,v7},使用者對專案的評分結合為R,使用者對專案的評分範圍是[0, 5]。R具體表示如下:
推薦系統的目標就是預測出符號“?”對應位置的分值。推薦系統基於這樣一個假設:使用者對專案的打分越高,表明使用者越喜歡。因此,預測出使用者對未評分專案的評分後,根據分值大小排序,把分值高的專案推薦給使用者。怎麼預測這些評分呢,方法大體上可以分為基於內容的推薦、協同過濾推薦和混合推薦三類,協同過濾演算法進一步劃分又可分為基於基於記憶體的推薦(memory-based)和基於模型的推薦(model-based),本文介紹的矩陣分解演算法屬於基於模型的推薦。
矩陣分解演算法的數學理論基礎是矩陣的行列變換。在《線性代數》中,我們知道矩陣A進行行變換相當於A左乘一個矩陣,矩陣A進行列變換等價於矩陣A右乘一個矩陣,因此矩陣A可以表示為A=PEQ=PQ(E是標準陣)。
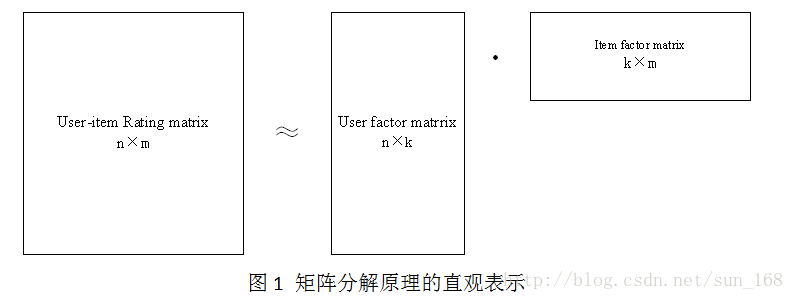
矩陣分解目標就是把使用者-專案評分矩陣R分解成使用者因子矩陣和專案因子矩陣乘的形式,即R=UV,這裡R是n×m, n =6, m =7,U是n×k,V是k×m。直觀地表示如下:
高維的使用者-專案評分矩陣分解成為兩個低維的使用者因子矩陣和專案因子矩陣,因此矩陣分解和PCA不同,不是為了降維。使用者i對專案j的評分r_ij =innerproduct(u_i, v_j),更一般的情況是r_ij =f(U_i, V_j),這裡為了介紹方便就是用u_i和v_j內積的形式。下面介紹評估低維矩陣乘積擬合評分矩陣的方法。
首先假設,使用者對專案的真實評分和預測評分之間的差服從高斯分佈,基於這一假設,可推匯出目標函式如下:
最後得到矩陣分解的目標函式如下:
從最終得到得目標函式可以直觀地理解,預測的分值就是儘量逼近真實的已知評分值。有了目標函式之後,下面就開始談優化方法了,通常的優化方法分為兩種:交叉最小二乘法(alternative least squares)和隨機梯度下降法(stochastic gradient descent)。
首先介紹交叉最小二乘法,之所以交叉最小二乘法能夠應用到這個目標函式主要是因為L對U和V都是凸函式。首先分別對使用者因子向量和專案因子向量求偏導,令偏導等於0求駐點,具體解法如下:
上面就是使用者因子向量和專案因子向量的更新公式,迭代更新公式即可找到可接受的區域性最優解。迭代終止的條件下面會講到。
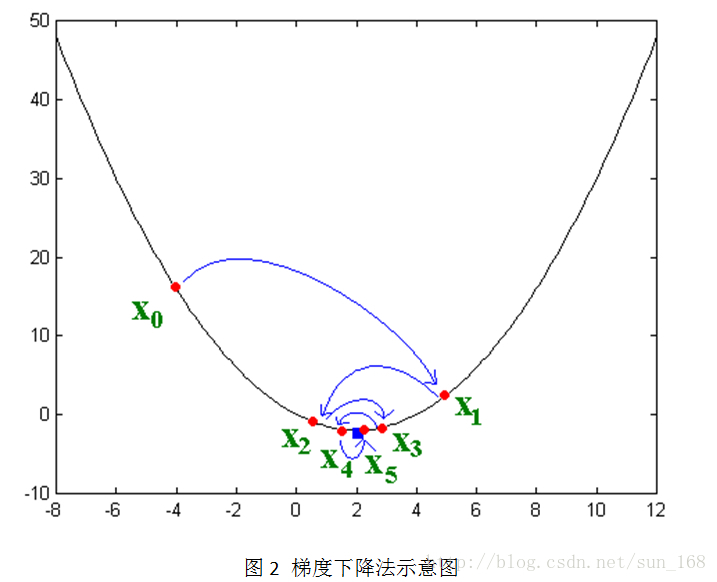
接下來講解隨機梯度下降法,這個方法應用的最多。大致思想是讓變數沿著目標函式負梯度的方向移動,直到移動到極小值點。直觀的表示如下:
其實負梯度的負方向,當函式是凸函式時是函式值減小的方向走;當函式是凹函式時是往函式值增大的方向移動。而矩陣分解的目標函式L是凸函式,因此,通過梯度下降法我們能夠得到目標函式L的極小值(理想情況是最小值)。
言歸正傳,通過上面的講解,我們可以獲取梯度下降演算法的因子矩陣更新公式,具體如下:
(3)和(4)中的γ指的是步長,也即是學習速率,它是一個超引數,需要調參確定。對於梯度見(1)和(2)。
下面說下迭代終止的條件。迭代終止的條件有很多種,就目前我瞭解的主要有
1) 設定一個閾值,當L函式值小於閾值時就停止迭代,不常用
2) 設定一個閾值,當前後兩次函式值變化絕對值小於閾值時,停止迭代
3) 設定固定迭代次數
另外還有一個問題,當用戶-專案評分矩陣R非常稀疏時,就會出現過擬合(overfitting)的問題,過擬合問題的解決方法就是正則化(regularization)。正則化其實就是在目標函式中加上使用者因子向量和專案因子向量的二範數,當然也可以加上一範數。至於加上一範數還是二範數要看具體情況,一範數會使很多因子為0,從而減小模型大小,而二範數則不會它只能使因子接近於0,而不能使其為0,關於這個的介紹可參考論文Regression Shrinkage and Selection via the Lasso。引入正則化項後目標函式變為:
(5)中λ_1和λ_2是指正則項的權重,這兩個值可以取一樣,具體取值也需要根據資料集調參得到。優化方法和前面一樣,只是梯度公式需要更新一下。
矩陣分解演算法目前在推薦系統中應用非常廣泛,對於使用RMSE作為評價指標的系統尤為明顯,因為矩陣分解的目標就是使RMSE取值最小。但矩陣分解有其弱點,就是解釋性差,不能很好為推薦結果做出解釋。
----------------------------------------------------------------------
概率的角度來預測使用者的評分,本文假設使用者和商品的特徵向量矩陣都符合高斯分佈,基於這個假設,使用者對商品的喜好程度就是一系列概率的組合問題,例如
為期望為μ,方差為σ的高斯分佈。Iij=1,如果使用者i選擇了商品j,否則為0。在此基礎上,本文通過對使用者的特徵向量加以限制,提出了一種新的演算法,並且該演算法要好於上述提到的演算法。
方法:
首先,本文假設預測使用者的喜好是一個概率組合問題:
其中使用者和商品的特徵向量都符合高斯分佈:
對上述的預測公式取對數,我們可以得到
優化公式(3)等同於直接優化下列的公式
為了把評分(例如1-5的評分)轉換為0-1,本文采用瞭如下辦法:
因此對應的預測公式變為
另外本文通過對使用者的特徵向量加以限制,即
那麼對應的評分預測函式為
其中W為某種權重矩陣,例如可以是相似度矩陣等等,同樣的,W也符合高斯分佈
實驗結果:
上圖是本文演算法與Netflix系統推薦演算法,SVD演算法的對比結果。首先,SVD演算法overfit比較嚴重,當epoch超過10時,SVD演算法就開始overfit了,其次constrained PMF要好於PMF演算法,而且該演算法比Netflix系統推薦演算法精度高7%左右。
另外本文也對比了,不同評分數目的RMSE的精度,如下圖所示:
可以看出,當評分比較少的時候,constrained PMF演算法的準確性就更加明顯,另外,如果採用電影的平均分來作為使用者的預測分值,當評分比較少的情況,這種演算法跟PMF和constrained PMF演算法差別不大,但是當評分比較多時,演算法的準確性差異就很明顯了
________________________________________________________________________________________________
4. 其他情況:
由於評分矩陣的稀疏性(因為每一個人只會對少數的物品進行評分),因此傳統的矩陣分解技術不能完成矩陣的分解,即使能分解,那樣計算複雜度太高,不現實。因此通常的方法是使用已存在評分計算出出預測誤差,然後使用梯度下降調整引數使得誤差最小。
首先說明一些符號的含義:戴帽子的rui表示預測u對i的打分,qi表示物品i每個特性的歸屬度向量,pu表示使用者u對每個特性的喜歡程度的向量。因此,物品的預測得分為:
下面我們就需要根據已有的資料計算誤差並修正q和p使得誤差最小,誤差的表示方式如下: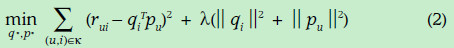
(2)式子可以利用評分矩陣中存在的評分資料,使用隨機梯度下降方法進行引數的優化,在此不做介紹。注意第二項是正則式,是為了防止過擬合,具體原理也不太清楚。
計算完闡述後們對於未知的專案就可以使用(1)式子評分。
上面的式子是最基本的矩陣分解思想,但實際情況下,卻並不是很好的衡量標準,比如有的網站中的使用者偏向評價高分;有一些使用者偏向評價高分(有的人比較寬容);有的物品被評價的分數偏高(也許由於等口碑原因)。因此在上面的式子中一般都會加入偏置項,u,bi,bu。綜合用下面的式子表示
結果預測式子變成如下:
誤差預測變成如下形式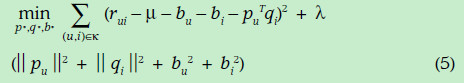
由於現實的評分矩陣特別稀疏,因此,為了使得資料更加稠密,下面加入了歷史的引述反饋資料(比如使用者瀏覽過瀏覽過某個電影就可以當做一定成的喜愛的正反饋),隱式反饋表現出來的偏好用下面的式子表示,其中xi表示歷史資料所表現出的偏好的向量,跟前面的向量維度相同。前面的權重表示這一項的可信任程度。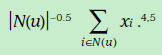
同樣,我們也可以使用使用者的標籤(比如年齡,性別,職業)推測使用者對每個因素的喜愛程度,形式化如下,ya表示標籤所表現出的偏好向量。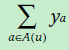
加入上面因素後的評分估計表示如下: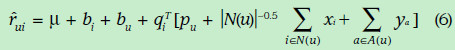
帶有時間因素的矩陣分解
現實生活中,我們每個人的愛好可能隨著時間的改變而改變,每個專案的平均評分也會改變。因此,專案的偏差(即專案高於平均分還是低於平均分)bi,使用者的評分習慣(即偏向於高分還是低分)bu,以及使用者的喜好矩陣pu都是時間的函式。為了更加準確的表達評分,都需要表示成為時間的函式形式,如下(這裡沒有考慮歷史標籤等資料):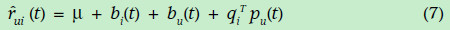
相關推薦
資料探勘基礎知識-矩陣(分解)
1. 矩陣知識: //特徵值,行列式,秩,對稱矩陣,單位矩陣,正定半正定,雅可比等等!! 正交矩陣: 如果:AA'=E(E為單位矩陣,A'表示“矩陣A的轉置矩陣”。)或A′A=E,則n階實矩陣A稱為正交矩陣, 若A為正交陣,則滿足以下條件: 1) AT是正交矩陣 2)(
NLP&資料探勘基礎知識
Basis(基礎): SSE(Sum of Squared Error, 平方誤差和) SAE(Sum of Absolute Error, 絕對誤差和) SRE(Sum of Relative Error, 相對誤差和) MSE(Mean Squared Error, 均方誤差) RMSE(R
資料探勘基本知識
背景 資料探勘解決的商業問題 客戶流失分析 交叉銷售 欺詐檢測 風險管理 客戶細分 廣告定位 銷售預測 資料探勘的任務 分類 基於一個可預測屬性把事例分成多個類別。有目標的資料探勘演算法稱為有監督
資料探勘基礎之統計學的分佈函式
本部落格根據非常好的excel資料而編寫,使用python語言操作,預計使用一週的時間更新完成。需要《非常好的excel資料》word文件,歡迎發郵件給[email protected],免費發放。 1、幾種常見的統計函式 2、分佈函式 ① ② ,求P{X=5
資料探勘基礎-2.中文分詞
一、中文分詞基礎 • 切開的開始位置對應位是1,否則對應位是0,來表示“有/意見/分歧”的bit內容是:11010,通過識別1後面幾個0,就可以知道有幾個字切在一塊。 • 還可以用一個分詞節點序列來表示切分方案,例如“有/意見/分歧”的分詞節點序列是{0,1,3,5}
資料探勘基礎之統計學的假設檢驗實驗
本部落格根據非常好的excel資料而編寫,使用python語言操作,預計使用一週的時間更新完成。需要《非常好的excel資料》word文件,歡迎發郵件給[email protected],免費發放。這篇部落格對應《非常好的excel資料》裡的第3章節。 1.假設檢驗實驗 1
資料探勘基礎導論學習筆記(五)
第五章 分類 其他分類 貝葉斯分類器 貝葉斯定理:把類的先驗知識和從資料中收集的新證據相結合的統計原理。 公式: P(Y|X)=P(X|Y)*P(Y)/P(X) X是屬性集,Y是類變數 把X和Y看成隨機變數,用P(Y|X)以概率的方式捕捉二者之間的關係,這個條件
《Python資料分析與挖掘實戰》筆記(一):資料探勘基礎
一、資料探勘的基本任務 利用分類與預測、聚類分析、關聯規則、時序模式、偏差檢測、智慧推薦等方法,幫助企業提取資料中蘊含的商業價值,提升企業的競爭力。 二、資料探勘建模過程 定義挖掘目標:任務目標和完
資料探勘基礎-1.文字相似度
一、文字相似度 相似度度量指的是計算個體間相似程度,一般使用距離來度量,相似度值越小,距離越大,相似度值越大,距離越小。在說明文字相似度概念和計算方式之前,先回顧下餘弦相似度。 1.餘弦相似度 衡量文字相似度最常用的方法是使用餘弦相似度。 – 空間中,兩個向量夾角的
python 資料探勘基礎 入門
一. 基於Python的資料探勘 基本架構 1. matplotlib, 圖形化 2. pandas,資料探勘的關鍵, 提供各種挖掘分析的演算法 3. numpy, 提供基本的統計 scipy, 提供各種數學公式 4. python common lib,py
【摘錄】大資料探勘與知識發現的應用領域
應用 資料探勘技術可以為決策、過程控制、資訊管理和查詢處理等任務提供服務,一個有趣的應用範例是“尿布與啤酒”的故事。為了分析哪些商品顧客最有可能一起購買,一家名叫 WalMart的公司利用自動資料探勘工具,對資料庫中的大量資料進行分析後,意外發現,跟尿布一起購買最多的商品
資料探勘工程師知識集錦
資料探勘的技術過程: 資料清理(消除噪音或不一致資料) 資料整合(多種資料來源可以組合在一起) 資料選擇(從資料庫中提取與分析任務相關的資料) 資料變換(資料變換或統一成適合挖掘的形式;如,通過彙總或聚集操作) 資料探勘(基本步驟,使用智慧方法提
【Mark Schmidt課件】機器學習與資料探勘——稀疏矩陣分解
本課件主要內容包括: 上次課程回顧:基於正交/序貫基的PCA 人眼的顏色對立 顏色對立表示法 應用:人臉檢測 特徵臉 VQ vs. PCA vs. NMF 面部表示 非負最小二乘法 稀疏性與非負最小
Python資料探勘課程 六.Numpy、Pandas和Matplotlib包基礎知識
前面幾篇文章採用的案例的方法進行介紹的,這篇文章主要介紹Python常用的擴充套件包,同時結合資料探勘相關知識介紹該包具體的用法,主要介紹Numpy、Pandas和Matplotlib三個包。目錄: 一.Python常用擴充套件包
資料探勘必備基礎知識
資料探勘,從字面上理解,就是在資料中找到有用的東西,哪些東西有用就要看具體的業務目標了。最簡單的就是統計應用了,比如電商資料,如淘寶統計過哪個省購買泳衣最多、哪個省的女生胸罩最大等,進一步,可以基於使用者的瀏覽、點選、收藏、購買等行為推斷使用者的年齡、性別、購買能力、愛好等能表示一個人的畫像,就相當於用這
【Python資料探勘課程】六.Numpy、Pandas和Matplotlib包基礎知識
前面幾篇文章採用的案例的方法進行介紹的,這篇文章主要介紹Python常用的擴充套件包,同時結合資料探勘相關知識介紹該包具體的用法,主要介紹Numpy、Pandas和Matplotlib三
寫給演算法/資料探勘面試小白的指南--計算機基礎知識
首先,關於計算機基礎知識,無非是考一些我們曾經學過的概念知識: 例如: 1.執行緒與程序的概念及區別 2.java的垃圾回收處理機制 3.hash表的原理 4.JVM的原理 下面來具體介紹一下具
零基礎學習大資料探勘的33個知識點整理
摘要: 下面是一些關於大資料探勘的知識點,今天和大家一起來學習一下。1. 資料、資訊和知識是廣義資料表現的不同形式。2. 主要知識模式型別有:廣義知識,關聯知識,類知識,預測型知識,特異型知識3. web挖掘研究的主要流派有:Web結構挖掘、Web使用挖掘、Web內容挖掘4. 一般地說,KD
資料探勘方面的研究必須用的那些知識!!!
關於資料探勘方面的研究,我原來也走過一些彎路。其實從資料探勘的起源可以發現,它並不是一門嶄新的科學,而是綜合了統計分析、機器學習、人工智慧、資料庫等諸多方面的研究成果而成,同時與專家系統、知識管理等研究方向不同的是,資料探勘更側重於應用的層面。 因此來說,資料探勘融合了相
零基礎入門大資料探勘之spark中的幾種map
今天再來說一下spark裡面的幾種map方法。前面的文章介紹過單純的map,但是spark還有幾種map值得對比一下,主要是下面幾種: map:普通的map flatMap:在普通map的基礎上多了一個操作,扁平化操作; mapPartitions:相對於分割槽P