漫步數學分析十八——緊集上連續函式的有界性

現在我們證明連續實值函式的一個重要性質，即有界定理。有界定理表明連續函式在緊集上是有界的並且在集合上的某些點取得最大值與最小值，準確的描述放到定理5中。

為了理解上面的結論，我們考慮非緊集上函式會發生什麼情況。首先，連續函式不一定是有界的，圖??? 給出的是開區間(0,1) 上的函式f(x)=1/x，隨著x越來越靠近0，函式變得任意大，但是不管怎樣f是連續的，因為f 是1 與連續函式x↦x 的商，而這個連續函式在(0,1) 上不等於0。

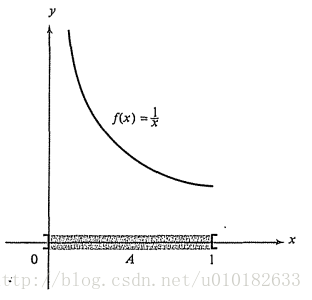
圖1

接下來，我們將說明即便函式是有界且連續的，在其定義域內也可能沒有最大值。圖???給出的是開區間[0,1)上的函式f(x)=x，這個函式沒有最大值，因為即便有無限個點靠近1，但是沒有任何一個點x

滿足f(x)=1。從這些例子中可以看出，對於緊集上的連續函式，這些情況都是不會發生的。

現在我們形式化成定理。

圖2

定理5 令A⊂Rn,f:A→R是連續函式，令K⊂A是緊集，那麼f在K上是有界的，即B={f(x)|x∈K}⊂R是有界集。進一步，存在點x0,x1∈K使得f(x0)=inf(B),f(x1)=sup(B)，我們稱sup(B)是f在K上的最大值，inf(B)是f在K上的最小值。

相比我們在微積分中學到的利用求導來定位極大值與極小值，這個結論要更近一步。例如R上的一些處處不可導的連續函式；這樣的函式我們無法用光滑曲線畫出來，所以直觀上不很明顯。

例1：給出一個緊集上不連續函式的例項，且這個函式無界。

解：將f:[0,1]→R定義成：如果x>0,f(x)=1/x，如果x=0,f(0)=0，很明顯這個函式與(0,1]上的函式1/x具有同樣的無界性。

例2：對[0,1]上的函式f(x)=x/(x2+1)，驗證定理5。

解：f(0)=0,f(1)=1/2，我們將驗證它的最大值在x=1處，最小值在x=0處。首先，因為x≥0,x2+1≥1，所以x/(x2+1)≥0，對於0≤x≤1,f(x)≥f(0)，因此0是最小值。接下來，注意到0≤(x−1)2=x2−2x+1，所以x2+1≥2x，故當≠0時，

xx2+1≤x2x=12

所以f(x)≤f(1)=12，即x=1是最大值點。

例3：說明定理5中的x0,