一種異常檢測演算法很難滿足所有的業務型別曲線。若想提高智慧告警的準確度，有必要對不同 曲線進行分類，以便於針對不同曲線，應用不同的異常檢測演算法。那麼一條曲線，到底包含了哪些資訊，可以幫助我們進行特徵提取呢？

資料描述

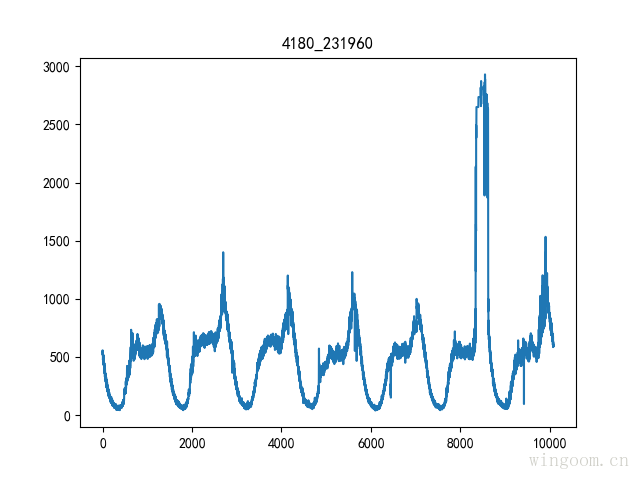
資料每分鐘一個點，一天1440個數據點，每天為一個週期，共7天資料。
測試資料為monitor資料，檢視4180,屬性231960.

資料去噪

常用的去噪方法有：3-σ去噪、移動中位數去噪。

3-σ去噪

資料點與均值相差超過3個標準差，則認為為噪點

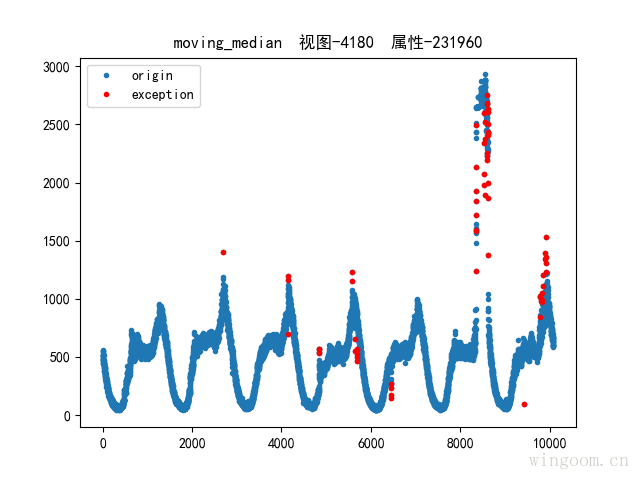
移動中位數去噪

用中位數代替均值，用中位數偏差代替標準差，避免極端異常值的影響。通過移動分段中位數，增強區域性異常點的探測。

import numpy as np
import pandas as pd
def median_noise_filter(df_data, threshold=15,rolling_median_window=50):
    exceptions = pd.Series()
    df_data['median'] = df_data['value'].rolling(window=rolling_median_window, center=True).median().fillna(method='bfill').fillna(
        method='ffill')
    difference = np.abs(df_data['value'
 
] - df_data['median'])
    median_difference = np.median(difference)
    if median_difference != 0:
        s = difference / float(median_difference)
        exceptions = s[s > threshold]
    return exceptions

移動中位數去噪需要選擇合適的滑動視窗和偏差閾值引數。3-σ簡單直接，但會受到極端值的影響

噪點填充

噪點填充為前一個和後一個正常點的均值

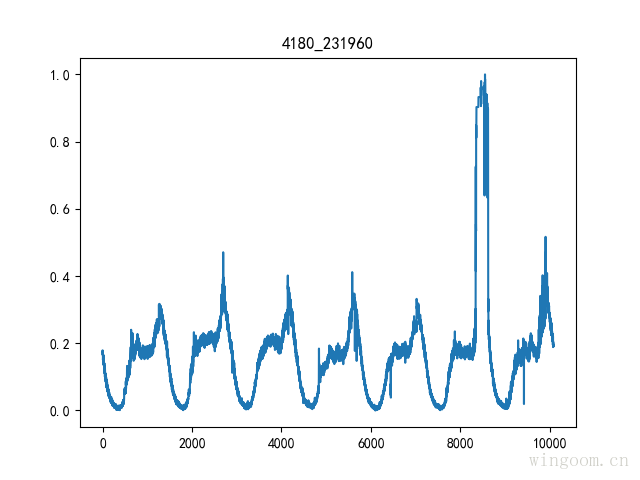
資料標準化(歸一化)

將資料按比例縮放，去除資料的單位限制，將其轉化為無量綱的純數值，專注於曲線的形狀識別，而不關心曲線上點數值的大小。

max-min標準化

對原始資料的一種線性變換，使原始資料對映到[0-1]之間，指將原始資料的最大值對映成1，是最大值歸一化

z-score標準化

根據原始資料的均值和標準差進行標準化,經過處理後的資料符合標準正態分佈，即均值為0，標準差為1.本質上是指將原始資料的標準差對映成1，是標準差歸一化。曲線數值表示該點與均值相差的標準差的資料量：

曲線值反映了資料點與均值相差的標準差個數。

統計特徵

中心位置

藉由中心位置，可以知道資料的一個平均情況。資料的中心位置可分為均值（Mean），中位數（Median），眾數（Mode）

• 均值：表示統計資料的一般水平。受到極端值影響
• 中位數：在 n 個數據由大到小排序後，位在中間的數字，不受極端值影響
• 眾數：一組資料中出現次數最多的資料值，不受極端值影響、非數值性資料同樣適用

發散程度

資料的發散程度可用極差或全距（R）、方差（Var）、標準差（STD）、變異係數（CV）來衡量.

零值率

零值所佔的比率，需要在max-min標準化前提前該特徵

波動率

波動率定義為7天波動率的中位數。
每天的波動率定義為該天資料標準化後的90分位值-10分位值：

或者可以直接採用wave_rate=quantile(x,0.9)−quantile(x,0.1)+1quantile(x,0.1)+1$wave\mathrm{\_}rate=\frac{quantile(x,0.9)-quantile(x,0.1)+1}{quantile(x,0.1)+1}$

偏度（Skewness）

偏度（偏態）是不對稱性的衡量。正態分佈的偏度是0，表示左右完美對稱。右偏度為正，左偏度為負.
Skewness 定義為：

峰度（kurtosis）

峰度（Kurtosis）衡量資料分佈相對於正態分佈，是否更尖或平坦。高峰度資料在均值附近有明顯峰值，下降很快並且有重尾（heavy tails）。低峰度在均值附近往往為平坦的頂部。
峰度（Kurtosis）定義為：