1設計目的、要求

   對龍格函式在區間[-1,1]上取的等距節點，分別作多項式插值、三次樣條插值和三次曲線擬合，畫出及各逼近函式的圖形，比較各結果。

2設計原理

（1）   多項式插值：利用拉格朗日多項式插值的方法，其主要原理是拉格朗日多項式，即：

表示待插值函式的個節點，

，其中；

（2）   三次樣條插值：三次樣條插值有三種方法，在本例中，我們選擇第一邊界條件下的樣條插值，即兩端一階導數已知的插值方法：

（3）三次曲線擬合：本題中採用最小二乘法的三次多項式擬合。最小二乘擬合是利用已知的資料得出一條直線或者曲線，使之在座標系上與已知資料之間的距離的平方和最小。在本題中，n= 10，故有11個點，以這11個點的和值為已知資料，進行三次多項式擬合，設該多項式為，該擬合曲線只需的值最小即可。

3採用軟體、裝置

   計算機、matlab軟體

4設計內容

1、多項式插值：

在區間上取的等距節點，帶入拉格朗日插值多項式中，求出各個節點的插值，並利用matlab軟體建立m函式，畫出其圖形。

在matlab中建立一個lagrange.m檔案，裡面程式碼如下：

%lagrange 函式

functiony=lagrange(x0,y0,x)

n=length(x0);m=length(x);

for i=1:m

    z=x(i);

    s=0.0;

    for k=1:n

        p=1.0;

        for j=1:n

            if j~=k

                p=p*(z-x0(j))/(x0(k)-x0(j));

            end

        end

        s=p*y0(k)+s;

    end

    y(i)=s;

end

建立一個polynomial.m檔案，用於多項式插值的實現，程式碼如下：

%lagrange插值

x=[-1:0.2:1];

y=1./(1+25*x.^2);

x0=[-1:0.02:1];

y0=lagrange(x,y,x0);

y1=1./(1+25*x0.^2);

plot(x0,y0,'--r')

%插值曲線

hold on

%原曲線

plot(x0,y1,'-b')

執行duoxiangshi.m檔案，得到如下圖形：

2、三次樣條插值：

所謂三次樣條插值多項式是一種分段函式，它在節點分成的每個小區間上是3次多項式，其在此區間上的表示式如下：

因此，只要確定了的值，就確定了整個表示式，的計算方法如下：

令：

則滿足如下個方程：

對於第一種邊界條件下有

如果令那麼解就可以為

求函式的二階導數：

>> syms x

>> f=sym(1/(1+25*x^2))

f =

1/(1+25*x^2)

>> diff(f)

ans =

-(50*x)/(25*x^2 + 1)^2

將函式的兩個端點，代入上面的式子中：

f’(-1)= 0.0740

f’(1)=-0.0740

求出從-1到1的n=10的等距節點，對應的x，y值

 對應m檔案程式碼如下：

for x=-1:0.2:1

   y=1/(1+25*x^2)

end

y =

得出

x=-1 -0.8  -0.6  -0.4 -0.2  0  0.2 0.4  0.6  0.8  1

y=0.0385 0.0588  0.1  0.2 0.5  1  0.5 0.2  0.1  0.0588 0.0385

編寫m檔案Three_Spline.m

x=linspace(-1,1,11);

y=1./(1+25*x.^2);

[m,p]=scyt1(x,y,0.0740,-0.0740);

hold on

x0=-1:0.01:1;

y0=1./(1+25*x0.^2);

plot(x0,y0,'--b')

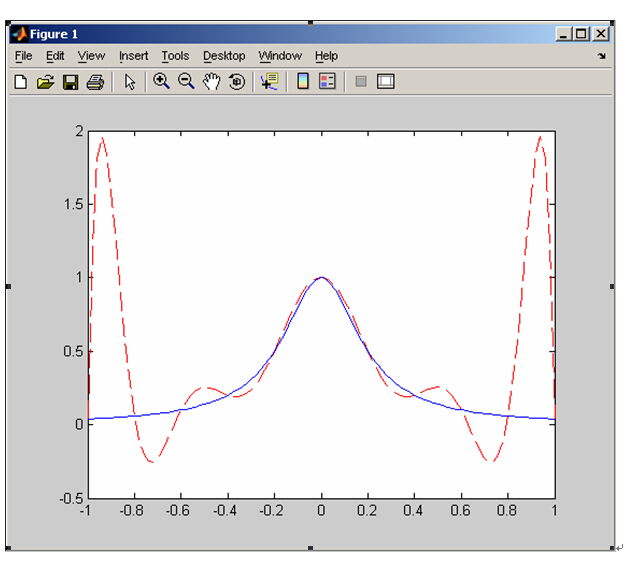
得到如下影象：

.

其中藍色曲線為原圖，紅色曲線為擬合後的影象。

3、三次曲線擬合：

這裡我們使用最小二乘法的3次擬合

建立一個Three_fitting .m檔案，程式碼如下：

%主要程式碼

x=[-1-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1];

y=[0.03850.0588 0.1 0.2 0.5 1 0.5 0.2 0.1 0.0588 0.0385];

a=polyfit(x,y,3);

x1=[-1:0.01:1];

y1=a(4)+a(3)*x1+a(2)*x1.^2+a(1)*x1.^3;

x0=[-1:0.01:1];

y0=1./(1+25*x0.^2)

%原曲線

plot(x0,y0,'-r')

holdon

%三次擬合曲線

plot(x1,y1,'-b')

上圖中，藍色部分為三次擬合曲線，紅色部分為原曲線

6結果分析

拉格朗日插值的優點是對於某一區域，不限於被估計點周圍，公式簡單易實施。一般認為n的次數越高，逼近的精度就越好，但在本題中，對龍格函式，中間部分插值效果比較好，而對於兩端，插值結果是非常不理想的，即龍格現象。樣條函式可以給出光滑的插值曲線，從本題中就能體現出來。從以上圖形可以看出，三次樣條插值的圖形是比較逼近於原圖的，收斂性相對而言是非常好的，但在本題中，僅將原區間分成10個等距區間，因此，逼近效果還不是特別理想，當我們將n增大時，插值後的曲線越逼近於原曲線。總的來說，三次樣條插值的穩定性比較好，收斂性比較強。

在這三種方法中，三次曲線擬合的效果是最差的，所得的圖形與原曲線差距甚遠。最小二乘法中，並不要求擬合後的曲線經過所有已知的點，只需要擬合多項式上的點在某種標準上與定點之間的差距最小即可，因此與原曲線的逼近程度是最差的。最小二乘法的多項式擬合只適用於多項式，而本題中的函式並不是一個多項式，因此，不建議使用最小二乘法擬合。

參考文獻:

[1] 李慶揚 王能超等.數值分析[M].清華大學出版社

[2] 吳振遠.科學計算實驗指導書 基於MATLAB數值分析[M]. 中國地質大學出版社

[3] 宋葉志. MATLAB數值分析與應用[M].機械工業出版社 , 2009.07

附錄

三次樣條插值主要程式碼：

function [m,p]=scyt1(x,y,df0,dfn)

n=length(x);

r=ones(n-1,1);

u=ones(n-1,1);

d=ones(n,1);

r(1)=1;

d(1)=6*((y(2)-y(1))/(x(2)-x(1))-df0)/(x(2)-x(1));

u(n-1)=1;

d(n)=6*(dfn-(y(n)-y(n-1))/(x(n)-x(n-1)))/(x(n)-x(n-1));

for k=2:n-1                  

   u(k-1)=(x(k)-x(k-1))/(x(k+1)-x(k-1)); r(k)=(x(k+1)-x(k))/(x(k+1)-x(k-1));

   d(k)=6*((y(k+1)-y(k))/(x(k+1)-x(k))-(y(k)-y(k-1))/(x(k)-x(k-1)))/(x(k+1)-x(k-1));

end

A=eye(n,n)*2;

for k=1:n-1

   A(k,k+1)=r(k);

   A(k+1,k)=u(k);

end

m=A\d;

ft=d(1);

syms t

for k=1:n-1           %求s(x)即插值多項式

   p(k,1)=m(k)/(6*(x(k+1)-x(k)));

   p(k,2)=m(k+1)/(6*(x(k+1)-x(k)));

   p(k,3)=(y(k)-m(k)*(x(k+1)-x(k))^2/6)/(x(k+1)-x(k));

   p(k,4)=(y(k+1)-m(k+1)*(x(k+1)-x(k))^2/6)/(x(k+1)-x(k));

 sx(k)=p(k,1)*(x(k+1)-t)^3+p(k,2)*(t-x(k))^3+p(k,3)*(x(k+1)-t)+p(k,4)*(t-x(k));

end

kmax=1000;

xt=linspace(x(1),x(n),kmax);

for i=1:n-1                   %出點xt對應的y值

   for k=1:kmax

     if x(i)<=xt(k)&xt(k)<=x(i+1)

        fx(k)=subs(sx(i),xt(k));

   end

end

end

plot(xt,fx,'r');  xlabel('x');

ylabel('y');  title('f');

text(x(fix(n/2)),y(fix(n/2)),'f')

hold on

plot(x,y,'*')

hold off