宣告：

Triplet Loss

在人臉識別中，Triplet loss被用來進行人臉嵌入的訓練。如果你對triplet loss很陌生，可以看一下吳恩達關於這一塊的課程。Triplet loss實現起來並不容易，特別是想要將它加到tensorflow的計算圖中。

通過本文，你講學到如何定義triplet loss，和進行triplets取樣的幾種策略。然後我將解釋如何在TensorFlow中使用線上triplets挖掘來實現Triplet loss。

Triplet loss和triplets挖掘

為什麼不用softmax

在監督學習中，我們通常都有一個有限大小的樣本類別集合，因此可以使用softmax和交叉熵來訓練網路。但是，有些情況下，我們的樣本類別集合很大，比如在人臉識別中，標籤集很大，而我們的任務僅僅是判斷兩個未見過的人臉是否來自同一個人。

Triplet loss就是專為上述任務設計的。它可以幫我們學習一種人臉嵌入，使得同一個人的人臉在嵌入空間中儘量接近，不同人的人臉在嵌入空間中儘量遠離。

定義損失

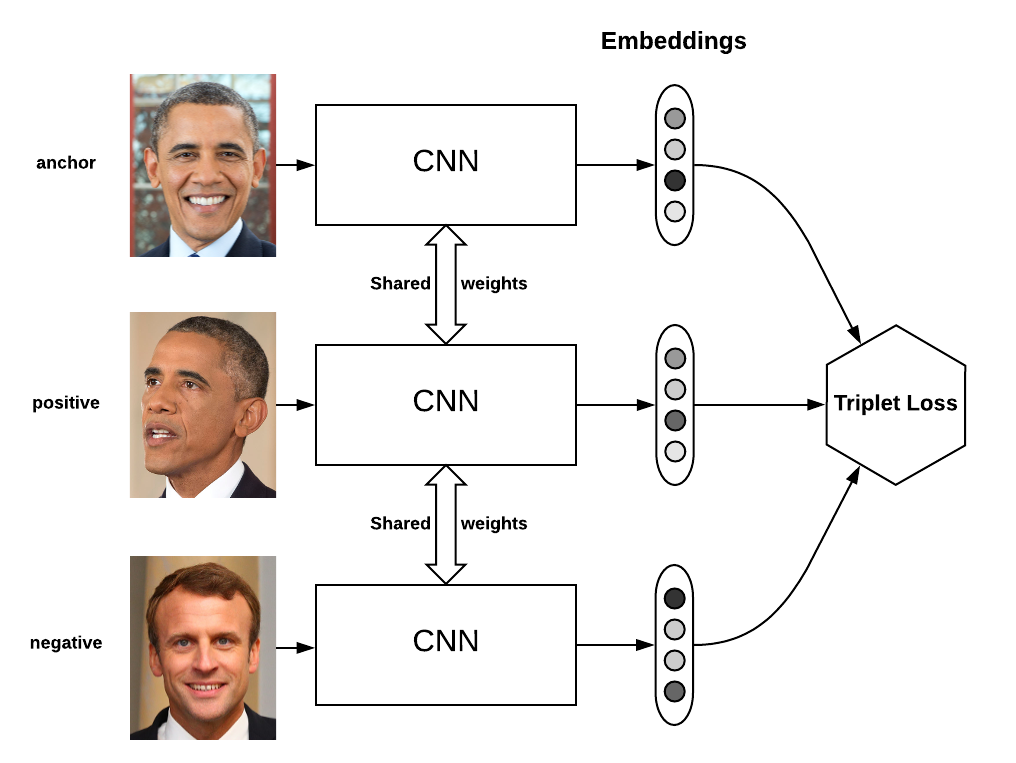
Triplet loss的目標：

• 使具有相同標籤的樣本在嵌入空間中儘量接近
• 使具有不同標籤的樣本在嵌入空間中儘量遠離

值得注意的一點是，如果只遵循以上兩點，最後嵌入空間中相同類別的樣本可能collapse到一個很小的圈子裡，即同一類別的樣本簇中樣本間的距離很小，不同類別的樣本簇之間也會偏小。因此，我們加入間隔(margin)的概念——跟SVM中的間隔意思差不多。只要不同類別樣本簇簡單距離大於這個間隔就闊以了。

Triplet可以理解為一個三元組，它由三部分組成：

• anchor在這裡我們翻譯為原點
• positive同類樣本點（與原點同類）
• negative異類樣本點

我們要求，在嵌入空間d$d$中，三元組(a,p,n)$(a,p,n)$滿足一下關係：

L=max(d(a,p)−d(a,n)+margin,0)$$L=max(d(a,p)-d(a,n)+margin,0)$$最小化該L$L$，則d(a,p)→0,d(a,n)>margin$d(a,p)\to 0,d(a,n)>margin$。

Triplets挖掘

基於前文定義的Triplet loss，可以將三元組分為一下三個類別：

• easy triplets：可以使loss = 0的三元組，即容易分辨的三元組
• hard triplets：d(a,n)<d(a,p)$d(a,n)<d(a,p)$的三元組，即一定會誤識別的三元組
• semi-hard triplets：d(a,p)<d(a,n)<d(a,p)+margin$d(a,p)<d(a,n)<d(a,p)+margin$的三元組，即處在模糊區域（關鍵區域）的三元組

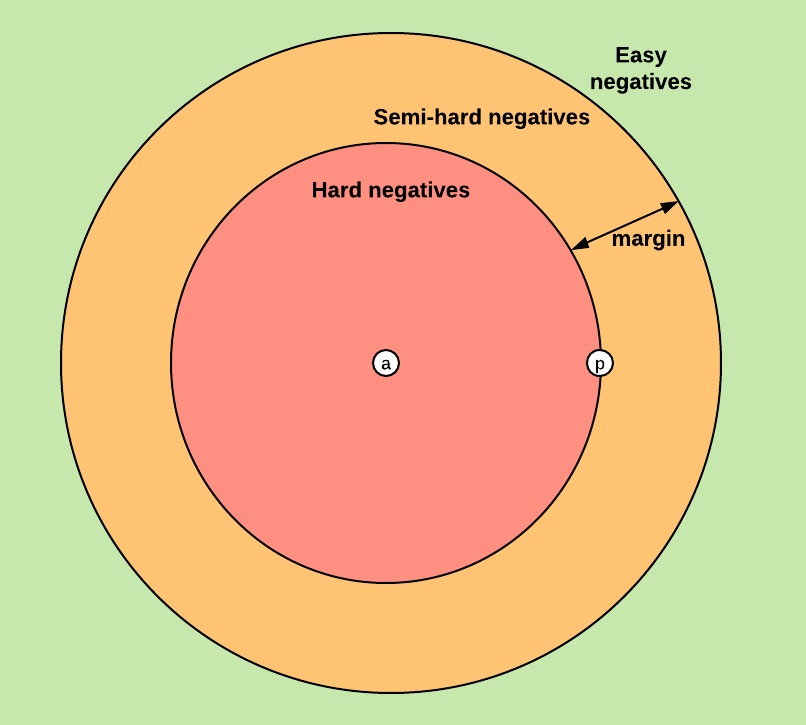
圖中，a為原點位置，p為同類樣本例子，不同顏色表示的區域表示異類樣本分佈於三元組類別的關係

顯然，中間的Semi-hard negatives樣本對我們網路模型的訓練至關重要。

離線和線上triplets挖掘

在網路訓練中，應儘可能使用Semi-hard negatives樣本，這一節將介紹如何選擇這些樣本。

離線

可以在每輪迭代之前從所有triplet中選擇semi-hard Triplet。也就是先對所有的訓練集計算嵌入表達(feature)，然後只選擇semi-hard triplets並以此為輸入訓練一次網路。

因為每輪訓練迭代之前都要遍歷所有triplet，計算它們的嵌入，所以offline挖掘triplet效率很低。

線上

假設有B個圖片（不是Triplet），也就是可以生成B個嵌入表達，那麼我們最多以此生成B3$B^3$個Triplet，當然大多數Triplet都不符合要求（不滿足一個同類一個異類的條件）。

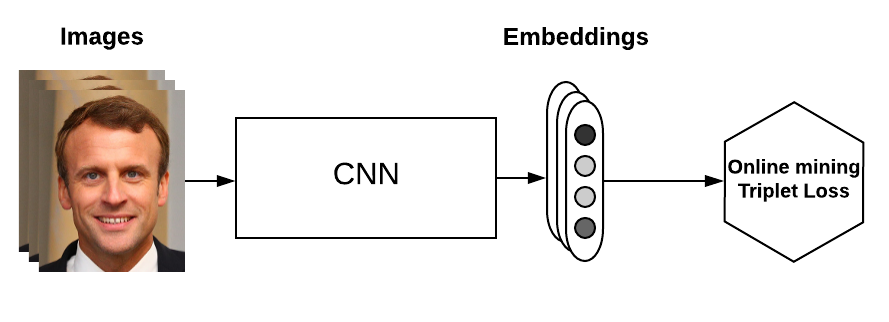
如上圖所示，網路輸入B個圖片，經過CNN得到embedding向量，在從中挑選semi-hard triplet。與離線挖掘相比，線上的方式有兩個優點：

• 只遍歷一個batch的圖片
• 在tansorflow計算圖中尋找semi-hard樣本

線上挖掘策略

線上挖掘實際上是從圖片的嵌入表示中生成Triplet。

對於包含B個圖片的banch，設i,j,k∈[1,B]$i,j,k\in [1,B]$，一個合格的Triplet要求：

• 樣本i， j不是同一個圖片且類別相同
• 樣本i, k類別不同

現在的問題就是如何從合格的Triplet中挑選semi-hard Triplet。

假設包含B個圖片的banch有P個不同的人組成，沒人有K個圖片，即B=PK$B=PK$。以K=4為例，有兩種線上挖掘策略：

• batch all：選擇所有合格的Triplet，對其中的hard和semi-hard Triplet的損失取均值
  
  • 這裡的關鍵在於消除easy Triplet的影響，因為easy Triplet的loss = 0，會拉低平均值
  • 合格的Triplet的數目為PK(K−1)(PK−K)$PK(K-1)(PK-K)$，即PK個原點，K-1個同類樣本，PK-K個異類樣本
• batch hard：遍歷所有原點(也就是banch中的所有樣本），選擇hardest同類樣本(d(a,p)$d(a,p)$最大的樣本)，選擇hardest異類樣本(d(a,n)$d(a,n)$最小的樣本）
  
  • 一共有PK個Triplet

雖然論文中說這種Triplet的選擇策略會大大提高模型的識別效果，但具體結果好壞還是取決於你的資料集。

簡單實現triplet loss

使用離線挖掘的策略，簡單實現以下Triplet loss如下：

anchor_output = ...  # shape [None, 128]
positive_output = ...  # shape [None, 128]
negative_output = ...  # shape [None, 128]

d_pos = tf.reduce_sum(tf.square(anchor_output - positive_output), 1)
d_neg = tf.reduce_sum(tf.square(anchor_output - negative_output), 1)

loss = tf.maximum(0.0, margin + d_pos - dneg)
loss = tf.reduce_mean(loss)

進階實現triplet loss

值得一提的是，在TensorFlow中有可以直接滴啊用的Triplet loss實現tf.contrib.losses.metric_learning.triplet_semihard_loss()。在本文中我們不用這個。

計算距離矩陣

計算距離的例子：
輸入的嵌入空間向量banch為：
⎡⎣⎢e1e2e3⎤⎦⎥$$\left[\begin{array}{c}{e}^1\\ e^2\\ e^3\end{array}\right]$$其中，e1$e^1$表示第一個嵌入向量，e2$e^2$表示第二個嵌入向量，e3$e^3$表示第三個嵌入向量，這些向量的特徵維度設為4，即e1=[e11,e12,e13,e14]$e^1=[e_1^1,e_2^1,e_3^1,e_4^1]$

根據||ei−ej||2$||e^i-e^j|{|}^2$計算嵌入向量之間的距離為：
⎡⎣⎢<e1,