假如我們有個這樣的網路：

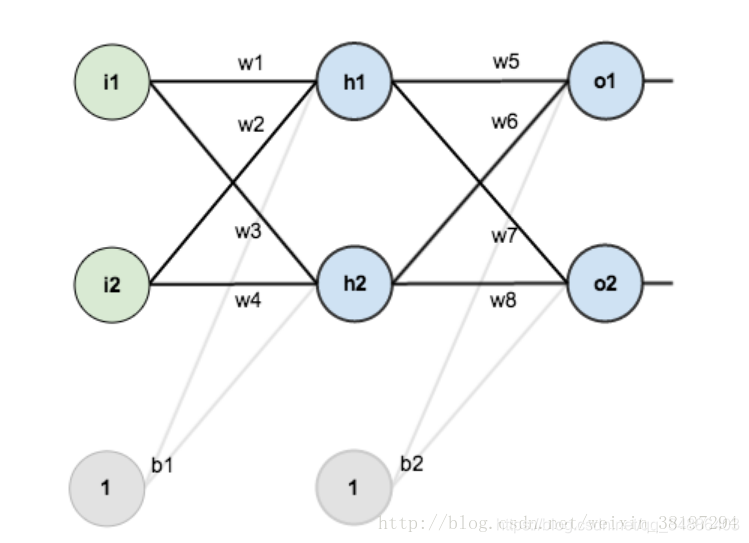
第一層是輸入層，包含兩個神經元i1，i2，和截距項b1；第二層是隱含層，包含兩個神經元h1,h2和截距項b2，第三層是輸出o1,o2，每條線上標的wi是層與層之間連線的權重，啟用函式我們預設為sigmoid函式。

其中，
輸入資料 i1=0.05，i2=0.10;
輸出資料 o1=0.01,o2=0.99;
初始權重 w1=0.15,w2=0.20,w3=0.25,w4=0.30，w5=0.40,w6=0.45,w7=0.50,w8=0.88

目標：給出輸入資料i1,i2(0.05和0.10)，使輸出儘可能與原始輸出o1,o2(0.01和0.99)接近。

Step 1：前向傳播
1.輸入層——>隱含層
$h$

1 = w 1 ∗ i 1 + w

2 ∗ I 2 + b 1 h1=w_1*i_1+w_2*I_2+b_1
$h1=0.15*0.05+0.2*0.1+0.35$

神經元h1的啟用：（此處用到啟用函式為sigmoid）
$active_{h1}=\frac{1}{e^{-h1}}=\frac{1}{1+e^{-0.3775}}=0.59326992$

同理，可計算出 $active_{h2}=0.596884378$

2.隱藏層——>輸出層
計算出o1和o2
$o_1=w_5*h_1+w_6*h_2+b_2$
$o_1=0.4*0.59326992+0.45*0.596884378+0.6=1.105905967$
啟用後
$active_{o1}=\frac{1}{1+e^{-1.105905967}}=0.75136507$

同理計算出o2
$active_{o2}=0.772928465$

這樣前向傳播的過程就結束了，我們得到輸出值為[0.75136079 , 0.772928465]，與實際值[0.01 , 0.99]相差還很遠，現在我們對誤差進行反向傳播，更新權值，重新計算輸出。

step 2 反向傳播
1.計算總誤差
$E_{total}=\sum\frac{1}{2}(target-output)^2$
但是有兩個輸出，所以分別計算o1和o2的誤差，總誤差為兩者之和：
$E_{active_{o1}}=\frac{1}{2}(0.01-0.75136507)^2$=0.274811083
KaTeX parse error: Expected '}', got 'EOF' at end of input: …2}}=0.023560026
$E_{tatol}=E_{active_{o1}}+E_{active_{o2}}=0.298371109$

2.反向傳播
我們使用反向傳播的目標是更新網路中的每個權重，使它們使實際輸出更接近目標輸出，從而最大限度地減少每個輸出神經元和整個網路的誤差。

考慮一下， 我們想知道 $w_5$的變化對總誤差的影響有多大，也就是（也就是 $w_5$的偏導數或者說是梯度）

通過鏈式求導：
$\frac{\partial E_{tatal}}{\partial w_5}=\frac{\partial E_{total}}{\partial active_{o1}}*\frac{\partial active_{o1}}{\partial o_1}*\frac{\partial o_1}{\partial w_5}$

相關推薦