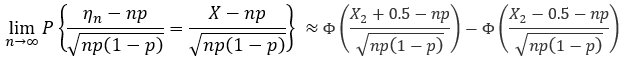二維隨機變數的條件分佈：

        定義：

              在兩個隨機變數 X,Y的情況下，給定Y 取某些值的情況下， 稱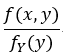：  是Y =y 的條件下X的條件概率密度；

         離散型隨機變數的條件分佈：

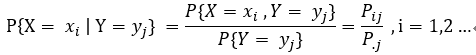                為在  Y =  條件下隨機變數 f(x,y) 的條件分佈律；

                 即  離散型隨機變數的條件分佈 = 聯合分佈 概率  /  邊緣分佈 概率（注意，可能會用到級數）；

         連續型隨機變數的條件分佈：

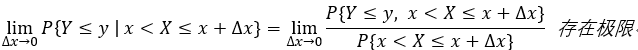                    稱 它為 極限 X= x的條件下，y的條件分佈函式；   記為： P{Y<= y | X = x} 或者

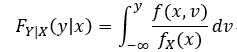：   且有：   即： 對條件概率密度 積分  可求得 條件分佈； 

           聯合分佈 可求 邊緣分佈 以及條件分佈；  邊緣分佈 與 條件分佈 也可求 聯合分佈； 

相互獨立的隨機變數：

       判定：   1. 變數間互不影響（離散型）；

                     2. 它們的兩個邊緣分佈 概率的乘積  等於聯合分佈 概率（連續型）

；

          即 對連續性隨機變數，若：  成立，則 這兩個隨機變數相互獨立；

數學期望：

     理解： 即 加權平均， 也即： 隨機變數可能取到的值與其概率之積 的累加；

     離散型隨機變數的數學期望： 

                設 X 分佈律  為： 

                 若 級數：  絕對收斂，則 稱 級數 的和 為 隨機變數X 的數學期望，記為： E(X);

                    E(x) =

     連續型隨機變數的數學期望：

           設連續型隨機變數 X 的概率密度 為 f(x) , 若積分 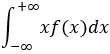  絕對收斂，則稱 積分  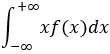為X 的數學期望，記為：E(X);   

             E(x) =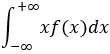

常見隨機變數的數學期望：

                   指數分佈:                       方差：   數學期望：θ;

                   均勻分佈：                    方差：     數學期望： 

                   二項分佈：   方差： np(1-p)        數學期望：  np

                   泊松分佈：                           方差： λ                  數學期望：λ

                   正態分佈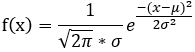：    方差： σ^2            數學期望： μ

數學期望的性質：

         1.   E(C)  =c;

         2.   E(2C) = 2E(C);

         3.   E(X+Y) = E(X)+E(Y);

         4.   若 X與 Y 相互獨立，則E(X*Y) = E(X)E(Y);

二維隨機變數的數學期望：

         E(XY) =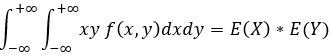

隨機變數的函式   的數學期望：

       離散型：  概率（權值）不變，相應的隨機量變化；

       連續型：  E( g(x) ) =    (大寫變小寫)

隨機變數的方差：

        常用來體現隨機變數取值 分散程度的量；

        定義：

              若X 是 一個隨機變數，有：   存在，稱： 為 X 的方差，記為 D(X);

             D(X) = E(X^2) - E^2(X),   即：方差  等於 隨機變數的平方 的期望 - 隨機變數的期望 的平方；

              為標準差  或 均方差，記為 ：σ(X);

        離散型隨機變數的方差計算：

              

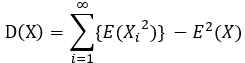
         連續型隨機變數的方差計算：

                  

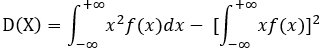
                或者：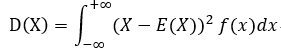  

         性質：

                1.  D(C)=0;   C 為常數；

                2.  若X,Y相互獨立， 則： D(X+- Y) = D(X) +- D(Y);

                3.  D(CX) =C^2 * D(X);

                4.  D(aX+b) = a^2 * D(X);

                5.  D(-X) = D(X);

        標準化變數：   的期望為 0， 方差為 1；

切比雪夫不等式:

        若隨機變數 X  具有  E(X) = μ，  方差 D(X) = σ^2 ,  則 對於任意  ε， 有不等式：

                

                 

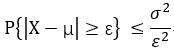
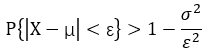
協方差:

        定義：

                Cov(X,Y) = E[ ( X-E(X) )*(Y-E(Y) ) ] ;

         計算公式:

                  若 X,Y 相互獨立， Cov(X,Y) = E[ X-E(X)] * E[Y-E(Y)] =0；

                  Cov(X,Y) = E(XY) - E(X)E(Y);

                  D(X+Y) = D(X) + D(Y) + 2 Cov(X,Y);

                  D(X-Y)  = D(X) + D(Y) -  2 Cov(X,Y);

          性質：

                  Cov(X,Y) = Cov(Y,X);

                  Cov(aX,bY) = ab Cov(X,Y);

                  Cov(X1+X2,Y) = Cov(X1,Y) + Cov(X2,Y);

                   若 X,Y相互獨立，則 E(X,Y) = E(X)*E(Y);

相關係數:

         定義:   

                  設 (X,Y) 為 二維隨機變數， D(X),D(Y) Cov(X,Y)  滿足： , 稱  為相關係數，  它反映了 X與 Y 相關關係的無量綱的關係；

                   當  =0 時， X 與 Y 不相關；

                 注意： 相互獨立 ==> ρ=0；   ρ=0  =/=>相互獨立；

         性質：

                -1 <=  <= 1;

             |  | =1 的充要條件:   存在 a,b ,使得 P(Y = a+bX) =1,即 X與 Y 幾乎處處有線性關係；

              >0  稱為 正相關；   <0  稱為 負相關；

              當 =1時，線性關係最強；

大數定理：

           伯努利大數定理：  包含 切比雪夫弱大數定理；  辛欽弱大數定理；

              概率是頻率的穩定值；

           拋硬幣實驗的數學意義：

                  

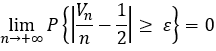
                它表示 頻率不一定 為 1/2， 但與  1/2 的偏差 >= ε的概率為0；

          切比雪夫弱大數定理：

                 設 x1,x2 ...  為獨立隨機變數序列，它們具有共同的數學期望μ， 並且 D(xi) <= C,  i=1,2 ...

                  且 對任意的 ε >0 ， 有 D(xi):

                       

           辛欽弱大數定理：

                   設  x1,x2  ... 相互獨立，服從同一分佈， 具有數學期望：  E(xi)  = μ，i=1,2, ...   , 且 對任意的 ε >0, 有：

                        

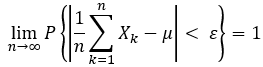
中心極限定理：

          作用:   用於研究正態分佈；   用於研究 獨立的隨機變數；

          定義：

                   把 隨機變數的和  的分佈 收斂於 正態分佈 這一類 定理  稱為  中心極限定理；

                   求和的標準化公式:    

          定理一：

                  隨機變數序列  獨立 且服從同一分佈時， 有：

                     

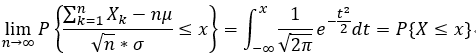
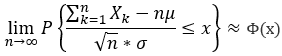                       ： 求概率的方法

            定理二（德莫佛-拉普拉斯方程）：

                      設隨機變數   (n=1,2,...)  服從引數為 n,p的二項分佈， 則對於任意x  ，恆有：

                  

                 它的修正方程：