一、例子

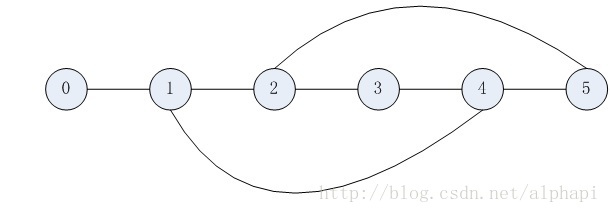
如上圖，節點0到節點5的最短路徑長度為3，有兩條最短路徑：

路徑1：0 — 1 — 4— 5

路徑2：0 — 1 — 2— 5

二、相關名稱

tempLadder：             儲存當前正在計算的路徑
canditStack：              儲存備選結點的棧
shortestLength：        最短路徑長度
startNode：                開始節點
endNode：                 終止節點
allShortestPath：    儲存startNod與endNode之間的所有的最短路徑。

三、約束條件：
1、如果節點node_a在路徑tempLadder中，從startNode起，node_a之前的各節點與node_a的距離分別是i,i-1,i-2....1，node_a與終結點的距離為shortestLength-i。

2、遍歷與node_a相鄰的各個節點，如果結點node_i已經在當前路徑tempLadder或者在canditStack中，或者與endNode的距離大於node_a與endNode的距離，則應該過濾掉node_i。

四：演算法過程：
step1、使用floyd計算結點間的最短距離

step2、輸入起點和終點的結點序號

step3、計算起點到終點間的所有最短距離

step3.1
 將startNode加入到tempLadder中，再將所有與startNode距離為1，與終結點距離為shortestLength-1的結點加入canditStack中，然後進入step3.2。

step3.2
當canditStack為空時，進入step4。

當canditStack不為空時，從canditStack中取出棧頂元素node，然後進入step3.3。

step3.3

如果node滿足條件1，則加入到tempLadder中，如果node與endNode距離為1，則同時將tempLadder加入到allShortestPath，tempLadder進行出棧，然後進入step3.4。

如果node不滿足條件1，tempLadder出棧，直到node滿足條件1為止，然後將node壓入tempLadder中，然後進入step3.4。

step3.4

遍歷與node距離為1的節點，如果滿足條件2，則過濾掉，否則，加入到canditStack中，進入step3.2。

step4

演算法終止。

五、程式

////////////////////////allshortpath.h////////////////////////////////
#ifndef H_FLOYD
#define H_FLOYD


#include <vector>


using namespace std;


#define MAX 1000
#define NODECOUNT 6  //結點數


typedef char VexType;


struct GraphMatrix
{
int n; //圖的頂點個數
VexType *vexs;//頂點資訊
int arcs[NODECOUNT][NODECOUNT];//邊資訊
};


struct ShortPath
{
int a[NODECOUNT][NODECOUNT];
int nextvex[NODECOUNT][NODECOUNT];
};


void floyd(GraphMatrix * pgraph, ShortPath * ppath);


void show_GraphMatirx(GraphMatrix * pgraph, int nodeCount);


void show_path(ShortPath * ppath, int nodeCount);


int shortestPath_2Nodes(int startNode, int endNode, ShortPath *ppath);


//判斷結點是否已經存在當前路徑中
int inVector(int nodeNum, vector<int> & tempvector, ShortPath *ppath);


int isPostNode(int nodeNum, int endNode, vector<int> & tempvector, ShortPath *ppath);


vector<vector<int>> getAllShortestPath(int startNode, int endNode, ShortPath *ppath, int nodeCount);


#endif

/////////////////////////////////////////allshortpath.cpp//////////////////////////////////////////////
#include <stdio.h>
#include <malloc.h>
#include <iostream>
#include <string>


#include "allshortpath.h"


void floyd(GraphMatrix * pgraph, ShortPath * ppath)
{
int i,j,k;
for ( i=0; i<pgraph->n; i++ )
{
for ( j=0; j<pgraph->n; j++ )
{
ppath->a[i][j] = pgraph->arcs[i][j];
}
}


for ( k=0; k<pgraph->n; k++ )
{
for ( i=0; i<pgraph->n; i++ )
{
for ( j=0; j<pgraph->n; j++ )
{
if ( (ppath->a[i][k]>=MAX)||(ppath->a[k][j]>=MAX) )
continue;


if ( ppath->a[i][j] > (ppath->a[i][k] + ppath->a[k][j]) )
{
ppath->a[i][j] = ppath->a[i][k] + ppath->a[k][j];
}
}
}
}
}


void show_GraphMatirx(GraphMatrix *pgraph, int nodeCount)
{
int i,j;


for ( i=0; i<nodeCount; i++ )
{
for ( j=0; j<nodeCount; j++ )
{
printf("%5d  ",pgraph->arcs[i][j]);
}
printf("\n");
}
printf("\n");
}


void show_path(ShortPath *ppath, int nodeCount)
{
int i, j;


for ( i=0; i<nodeCount; i++ )
{
for ( j=0; j<nodeCount; j++ )
{
printf("%5d ", ppath->a[i][j]);
}
printf("\n");
}
printf("\n");
}


int shortestPath_2Nodes(int startNode, int endNode, ShortPath *ppath)
{
int distance = ppath->a[startNode][endNode];
return distance;
}


vector<vector<int>> getAllShortestPath(int startNode, int endNode, ShortPath *ppath, int nodeCount)
{
int nodeNum = 0;
int tempFromStack;
int tempFromLadder;
int shortestLength;


vector<int> canditNodeStack;
vector<int> tempLadder;
vector<vector<int>> resultvector;


if ( startNode == endNode )
{
return resultvector;
}

tempLadder.push_back(startNode);
if ( ppath->a[startNode][endNode] == 1 )
{
tempLadder.push_back(endNode);
resultvector.push_back(tempLadder);
return resultvector;
}

shortestLength = shortestPath_2Nodes(startNode, endNode, ppath);


for ( nodeNum = 0; nodeNum < nodeCount; nodeNum++ )
{
if ( shortestPath_2Nodes(nodeNum, startNode, ppath) == 1 )
{
canditNodeStack.push_back(nodeNum);
}
}


while ( canditNodeStack.size() > 0 )
{
tempFromStack = canditNodeStack.back(); 
canditNodeStack.pop_back();

int d_temp_end = shortestPath_2Nodes(tempFromStack, endNode, ppath);

if ( d_temp_end == 0 && tempLadder.size() == shortestLength )
{
tempLadder.push_back(tempFromStack);
resultvector.push_back(tempLadder);
tempLadder.pop_back();
}
else
{
if ( isPostNode(tempFromStack, endNode, tempLadder, ppath) == 1 )
{
if ( tempLadder.size() <= shortestLength )
{
tempLadder.push_back(tempFromStack);
}
}
else
{
while ( tempLadder.size() > 0 && tempLadder.back() != startNode )
{
tempLadder.pop_back();


if ( isPostNode(tempFromStack, endNode, tempLadder, ppath) == 1 )
{
tempLadder.push_back(tempFromStack);
break;
}


}
}
}


for ( nodeNum = 0; nodeNum < nodeCount; nodeNum++ )
{
int i2 = shortestPath_2Nodes(tempFromStack, nodeNum, ppath); 
int i3 = shortestPath_2Nodes(endNode, nodeNum, ppath);
if ( i2 == 1 && d_temp_end > i3 && !inVector(nodeNum, canditNodeStack, ppath) && !inVector(nodeNum, tempLadder, ppath))
{
canditNodeStack.push_back(nodeNum);
}
}
}


return resultvector;


}


int inVector(int nodeNum, vector<int> & tempvector, ShortPath *ppath)
{
int exist = 0;
vector<int>::iterator it;
for ( it=tempvector.begin(); it!=tempvector.end(); it++ )
{


if(shortestPath_2Nodes(*it, nodeNum, ppath)==0)
{
exist = 1;
break;
}
}


return exist;


}


int isPostNode(int nodeNum, int endNode, vector<int> & tempvector, ShortPath *ppath)
{
if ( nodeNum == tempvector.back() )
{
return 0;
}


int flag = 1;
int d_temp_end = shortestPath_2Nodes(nodeNum, endNode, ppath);
int d_back_end = shortestPath_2Nodes(tempvector.back(), endNode, ppath);


if ( d_temp_end >= d_back_end )
{
return 0;
}


for ( int i = tempvector.size() - 1; i >= 0; i-- )
{
if ( shortestPath_2Nodes(nodeNum, tempvector.at(i), ppath) != (tempvector.size() - i) )
{
flag = 0;
}


}


return flag;


}

////////////////////////main.cpp////////////////////////////////////
#include <set>
#include <iostream>
#include <vector>


#include "allshortpath.h"


using namespace std;


void CalAllShortestPath()
{
int i=0;
int j=0;


GraphMatrix *pgraph = (GraphMatrix *)malloc(sizeof(struct GraphMatrix));
ShortPath   *ppath  = (ShortPath *)malloc(sizeof(struct ShortPath));


if ( pgraph==NULL || ppath==NULL )
{
return;
}


pgraph->n = NODECOUNT;


////////////////////初始化無向無權圖的鄰接矩陣///////////////////////////
int arcs[NODECOUNT][NODECOUNT]={0,1,MAX,MAX,MAX,MAX,  1,0,1,MAX,1,MAX,  MAX,1,0,1,MAX,1,  MAX,MAX,1,0,1,MAX,  MAX,1,MAX,1,0,1,  MAX,MAX,1,MAX,1,0};
//int arcs[POINTNUM][POINTNUM]={0,1,1,MAX,1,MAX,MAX,MAX,  1,0,1,1,MAX,MAX,MAX,MAX,  1,1,0,1,MAX,MAX,MAX,MAX,  MAX,1,1,0,MAX,1,MAX,MAX,  1,MAX,MAX,MAX,0,MAX,1,1,  MAX,MAX,MAX,1,MAX,0,1,1, MAX,MAX,MAX,MAX,1,1,0,1, MAX,MAX,MAX,MAX,1,1,1,0};

for ( i = 0; i < NODECOUNT; i++ )
{
for ( j = 0; j < NODECOUNT; j++ )
{
pgraph->arcs[i][j] = arcs[i][j];
}
}


show_GraphMatirx(pgraph, NODECOUNT);


floyd(pgraph, ppath);


show_path(ppath, NODECOUNT);
int startNode = 5;
int endNod = 0;
vector<vector<int>> result = getAllShortestPath(startNode, endNod, ppath, NODECOUNT);
vector<int> eachone;
vector<int>::iterator eachI;
set<int>::iterator it;
vector<vector<int>>::iterator resultIt;


for ( resultIt=result.begin(); resultIt!=result.end(); resultIt++ )
{
eachone = *resultIt;


for ( eachI=eachone.begin(); eachI!=eachone.end(); eachI++ )
{
cout<<*eachI<<" ";
}


cout<<endl;
}


}


int main()
{
CalAllShortestPath();

system("pause");


return 0;
}