社群發現(Community Detection)演算法
作者: peghoty
出處: http://blog.csdn.net/peghoty/article/details/9286905
社群發現(Community Detection)演算法用來發現網路中的社群結構,也可以看做是一種聚類演算法。
以下是我的一個 PPT 報告,分享給大家。
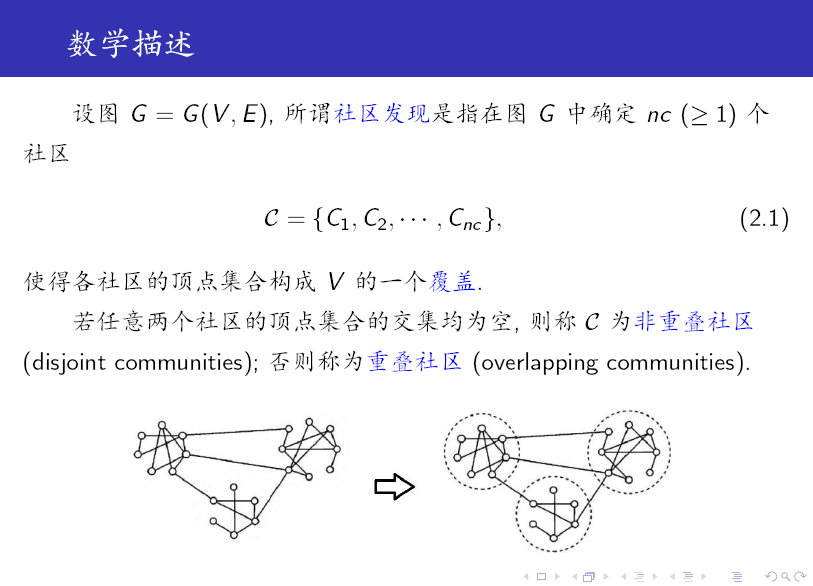
從上述定義可以看出:社群是一個比較含糊的概念,只給出了一個定性的刻畫。
另外需要注意的是,社群是一個子圖,包含頂點和邊。
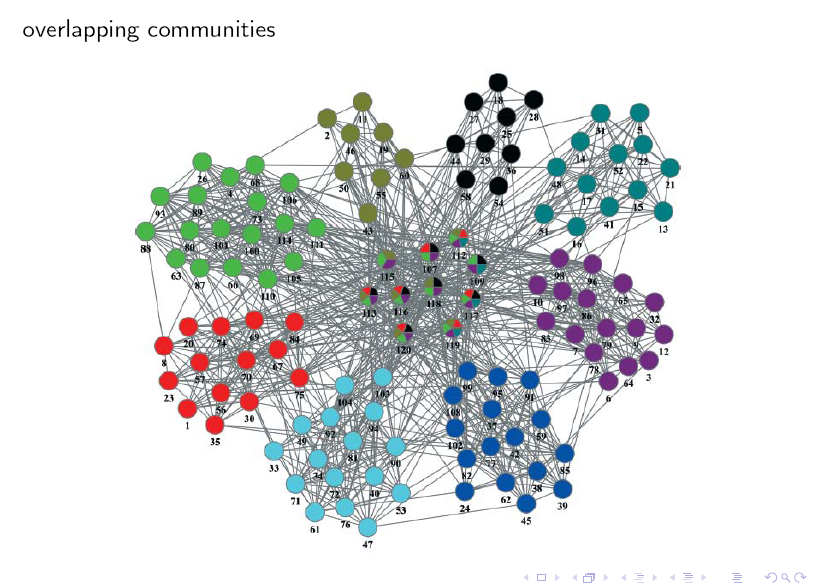
下面我們以新浪微博使用者對應的網路圖為例,來介紹相應的社群發現演算法。
這裡在相互關注的使用者之間建立連線關係,主要是為了簡化模型,此時對應的圖為無向圖。
當然,我們也可以採用單向關注來建邊,此時將對應有向圖。
這個定義看起來很拗口,但通過層層推導,可以得到如下 (4.2)的數學表示式。定義中的隨機網路也稱為Null Model
the null model used has so far been a random graph with the same number of nodes, the same number of edges and the same degree distribution as in the original graph, but with links among nodes randomly placed.
注意,(4.2) 是針對無向圖的,因此這裡的 m 表示無向邊的條數,即若節點 i 和節點 j 有邊相連,則節點 (i, j) 對 m 只貢獻一條邊。
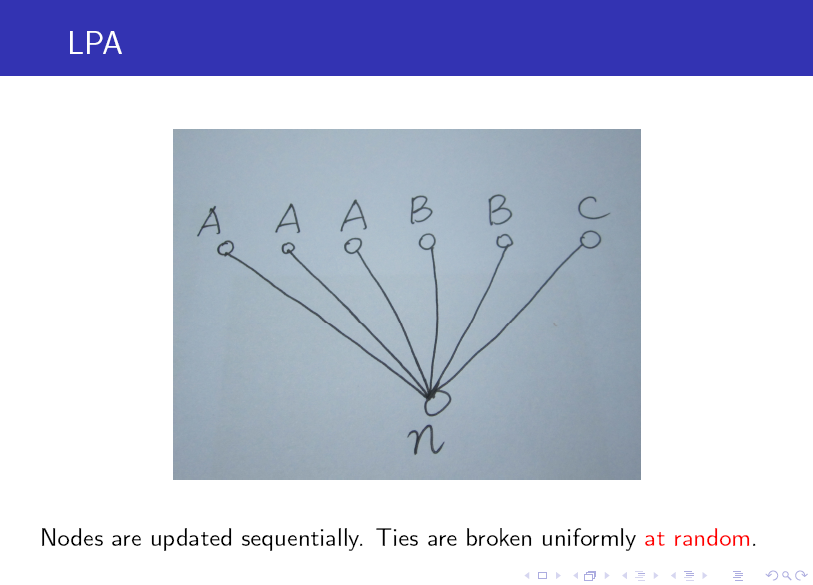
標籤傳播演算法(LPA)的做法比較簡單:
第一步: 為所有節點指定一個唯一的標籤;
第二步: 逐輪重新整理所有節點的標籤,直到達到收斂要求為止。對於每一輪重新整理,節點標籤重新整理的規則如下:
對於某一個節點,考察其所有鄰居節點的標籤,並進行統計,將出現個數最多的那個標籤賦給當前節點。當個數最多的標籤不唯一時,隨機選一個。
注:演算法中的記號 N_n^k 表示節點 n 的鄰居中標籤為 k 的所有節點構成的集合。
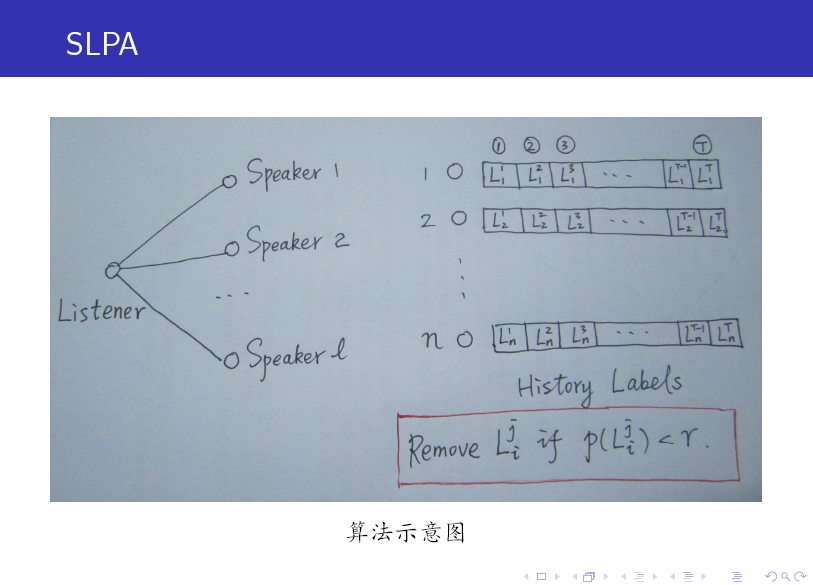
SLPA 中引入了 Listener 和 Speaker 兩個比較形象的概念,你可以這麼來理解:在重新整理節點標籤的過程中,任意選取一個節點作為 listener,則其所有鄰居節點就是它的 speaker 了,speaker 通常不止一個,一大群 speaker 在七嘴八舌時,listener 到底該聽誰的呢?這時我們就需要制定一個規則。
在 LPA 中,我們以出現次數最多的標籤來做決斷,其實這就是一種規則。只不過在 SLPA 框架裡,規則的選取比較多罷了(可以由使用者指定)。
當然,與 LPA 相比,SLPA 最大的特點在於:它會記錄每一個節點在重新整理迭代過程中的歷史標籤序列(例如迭代 T 次,則每個節點將儲存一個長度為 T 的序列,如上圖所示),當迭代停止後,對每一個節點歷史標籤序列中各(互異)標籤出現的頻率做統計,按照某一給定的閥值過濾掉那些出現頻率小的標籤,剩下的即為該節點的標籤(通常有多個)。
SLPA 後來被作者改名為 GANXiS,且軟體包仍在不斷更新中......
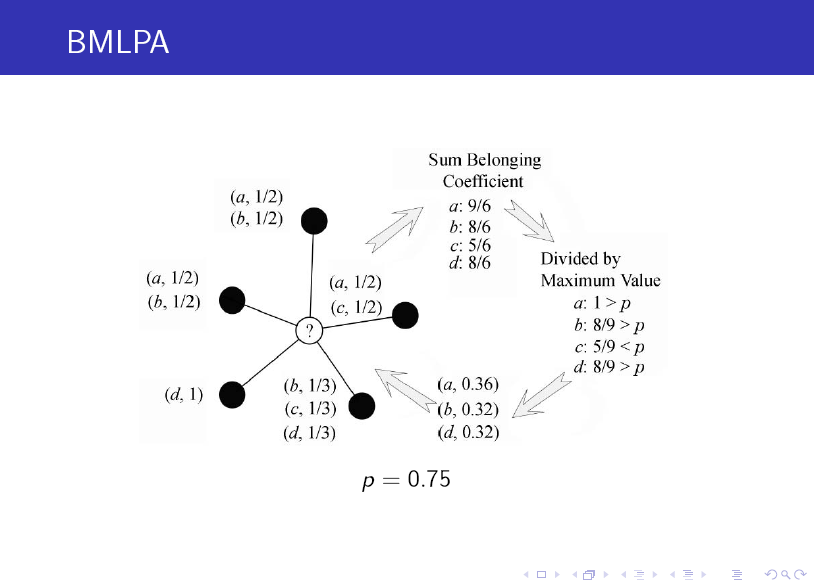
這裡對上面的圖做個簡單介紹:帶問號的節點是待確定標籤的節點,黑色實心點為其鄰居節點,它們的標籤是已知的,注意標籤均是由二元數對的序列構成的,序列中每一個元素的第一個分量表示其標籤,第二個分量表示該節點屬於該標籤對應社群的可能性(或者說概率,叫做 belonging coefficent),因此對於每個節點,其概率之和等於 1。
我們按照以下步驟來確定帶問號節點的標籤:
1. 獲取鄰居節點中所有的互異(distinct) 標籤列表,並累加相應的 belonging coefficent 值。
2. 對 belonging coefficent 值列表做歸一化,即將列表中每個標籤的 belonging coefficent 值除以 C1 (C1 為列表中 belonging coefficent 值的最大值)。
3. 過濾。若列表中歸一化後的 belonging coefficent 值(已經介於 0,1 之間)小於某一閥值 p (事先指定的引數),則將對應的二元組從列表中刪除。
4. 再一次做歸一化。由於過濾後,剩餘列表中的各 belonging coefficent 值之和不一定等於 1,因此,需要將每個 belonging coefficent 值除以 C2 (C2 表示各 belonging coefficent 值之和)。
經過上述四步,列表中的標籤即確定為帶問號節點的標籤。
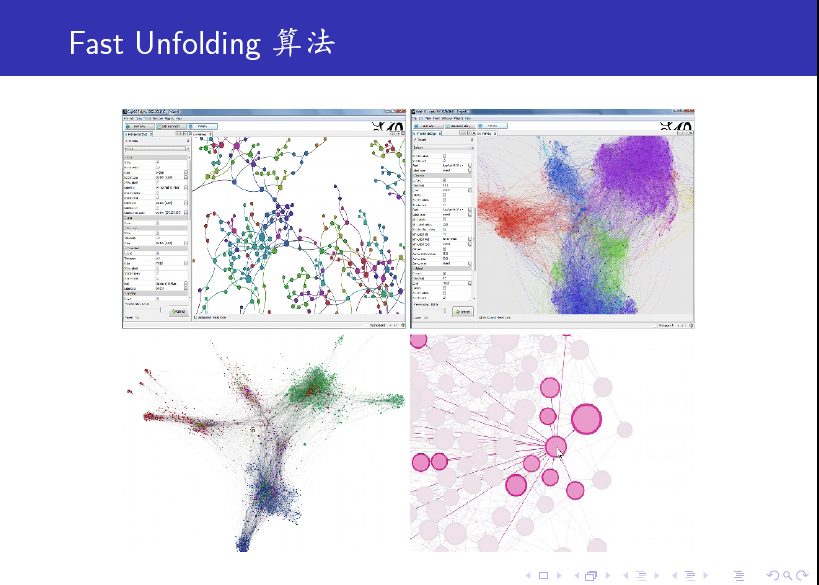
這裡,我們對 Fast Unfolding 演算法做一個簡要介紹,它分為以下兩個階段:
第一個階段:首先將每個節點指定到唯一的一個社群,然後按順序將節點在這些社群間進行移動。怎麼移動呢?以上圖中的節點 i 為例,它有三個鄰居節點 j1, j2, j3,我們分別嘗試將節點 i 移動到 j1, j2, j3 所在的社群,並計算相應的 modularity 變化值,哪個變化值最大就將節點 i 移動到相應的社群中去(當然,這裡我們要求最大的 modularity 變化值要為正,如果變化值均為負,則節點 i 保持不動)。按照這個方法反覆迭代,直到網路中任何節點的移動都不能再改善總的 modularity 值為止。
第二個階段:將第一個階段得到的社群視為新的“節點”(一個社群對應一個),重新構造子圖,兩個新“節點”之間邊的權值為相應兩個社群之間各邊的權值的總和。
我們將上述兩個階段合起來稱為一個 pass,顯然,這個 pass 可以繼續下去。
從上述描述我們可以看出,這種演算法包含了一種 hierarchy 結構,正如對一個學校的所有初中生進行聚合一樣,首先我們可以將他們按照班級來聚合,進一步還可以在此基礎上按照年級來聚合,兩次聚合都可以看做是一個社群發現結果,就看你想要聚合到什麼層次與程度。
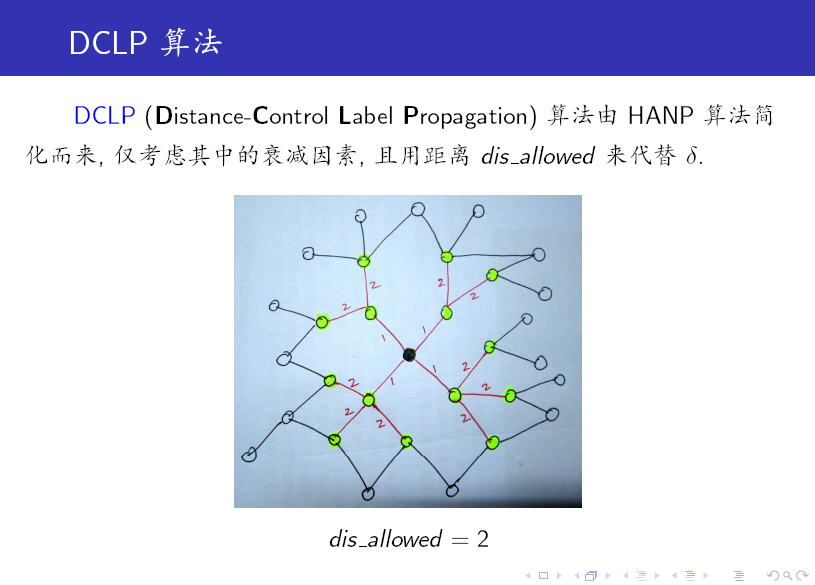
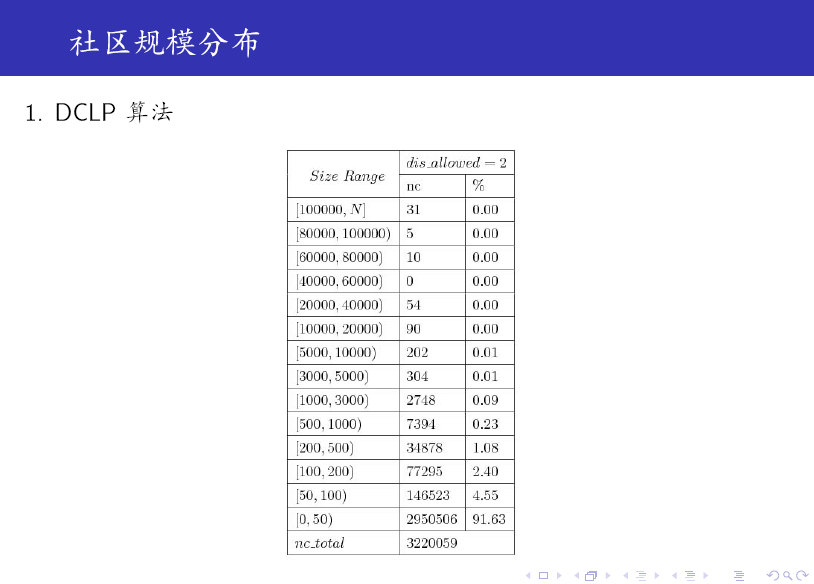
DCLP 演算法是 LPA 的一個變種,它引入了一個引數來限制每一個標籤的傳播範圍,這樣可有效控制 Monster (非常大的 community,遠大於其他 community)的產生。
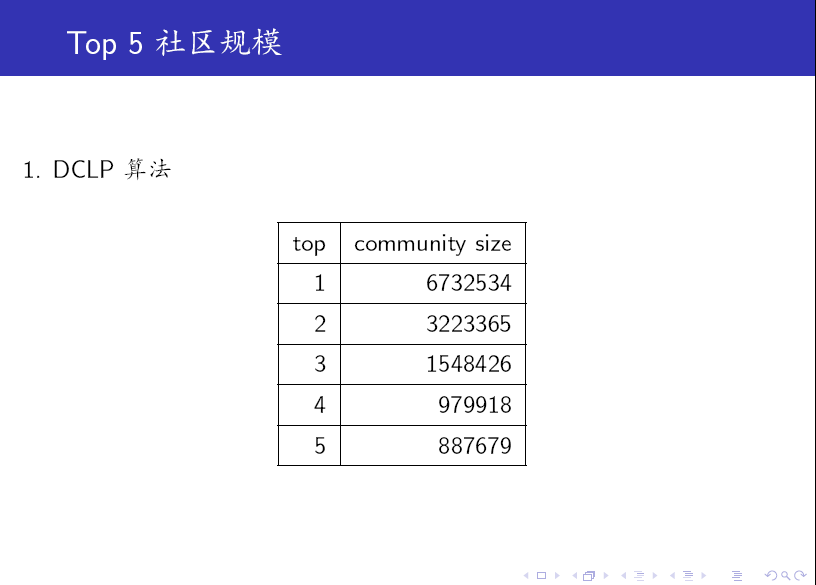
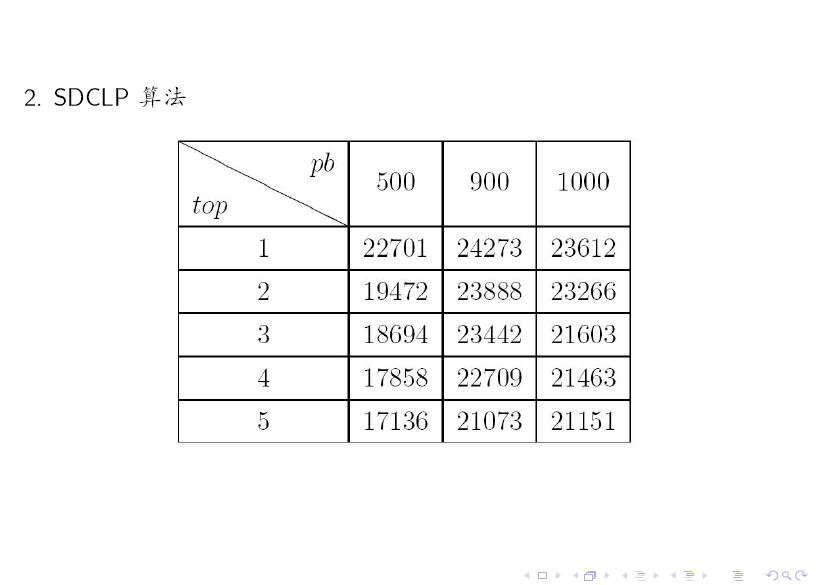
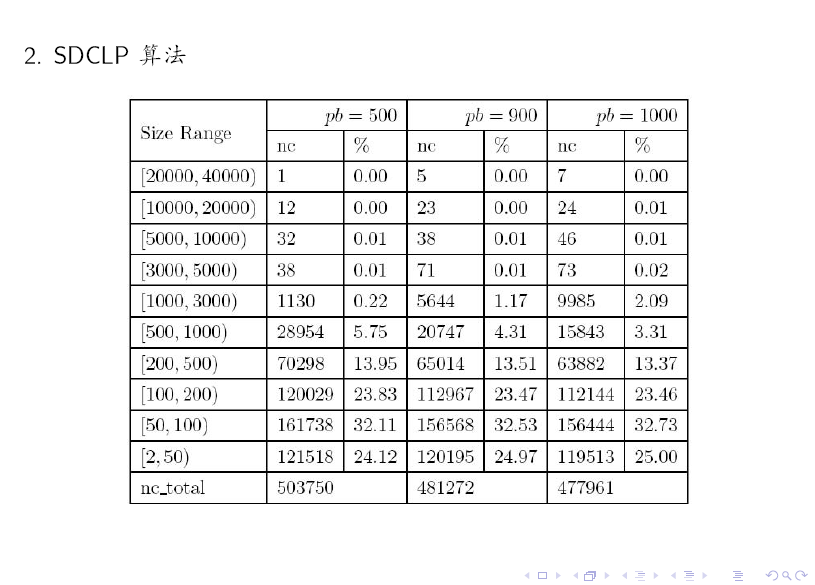
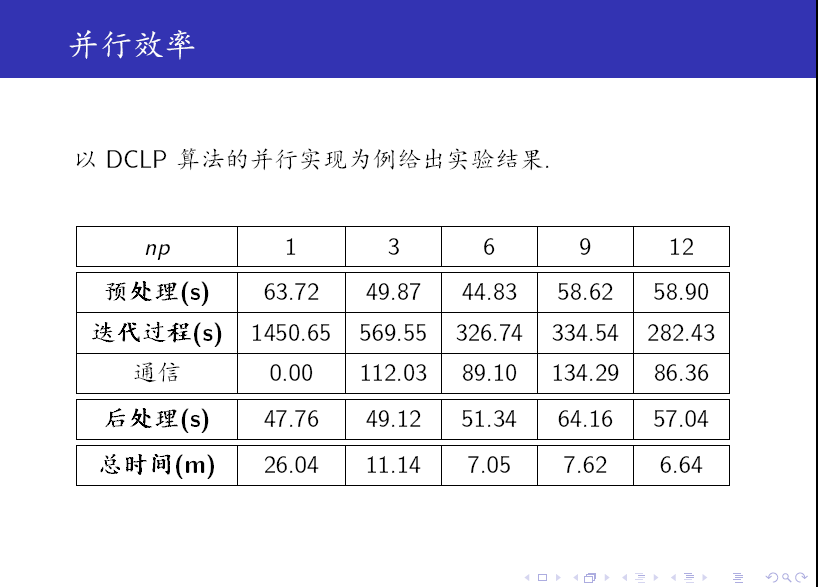
最後,我們給出一些實驗結果。
對比上述兩個表格可知:SDCLP 演算法得到的 top 5 社群更為均勻。