簡單易懂的迷宮走法--棧應用(c++)
哈嘍~小夥伴們,你們帥氣的阿俊又回來啦,他有好東西和你們分享哦,那就是困擾了他好久的迷宮問題。感覺自己走迷宮時簡單得很,可讓計算機走咋這麼難哩,我明白了,一定是因為計算機太笨了,真是笨死了,啥都要人家一步步教他咋做,還想取代人?路漫漫其修遠兮哦,嘿嘿嘿,那我們看看咋教他走迷宮吧!
如果學習過資料結構或圖論的小夥伴應該聽過深度/廣度優先搜尋演算法,這兩個演算法可是圖論中大多數演算法的基礎,非常重要哦。
圖可以用線代利器–鄰接矩陣儲存,而迷宮地圖也是可以用矩陣儲存喲,1表示牆,0表示通路。這樣迷宮求解問題就等價於指定深搜起點(迷宮入口),在深搜搜索過程中遇到指定終點(迷宮出口)就立即停止,因為它找到一條通路啦
深搜思想比較簡單,就一句話,當前點只要有鄰接點,就走下去;無鄰接點,往回退。重複判斷,直到遍歷完所有點。
這是典型的遞迴,不過遞迴雖然寫起來簡潔明瞭,但是卻不是太好寫,而且出錯時難以除錯,效率也不是太高,於是我們想到了用棧來實現深搜,彌補了遞迴的三個缺點,但可能程式碼量大一些,不過沒關係,黑貓,白貓,抓到老鼠就是好貓,那咱們看看如何用棧實現迷宮求解吧
先給你們看看區域性效果圖,饞哭你們,嘿嘿嘿
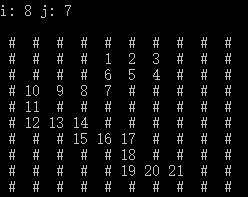
演算法描述
多說無益,咱們直接上圖吧
核心處理流程圖
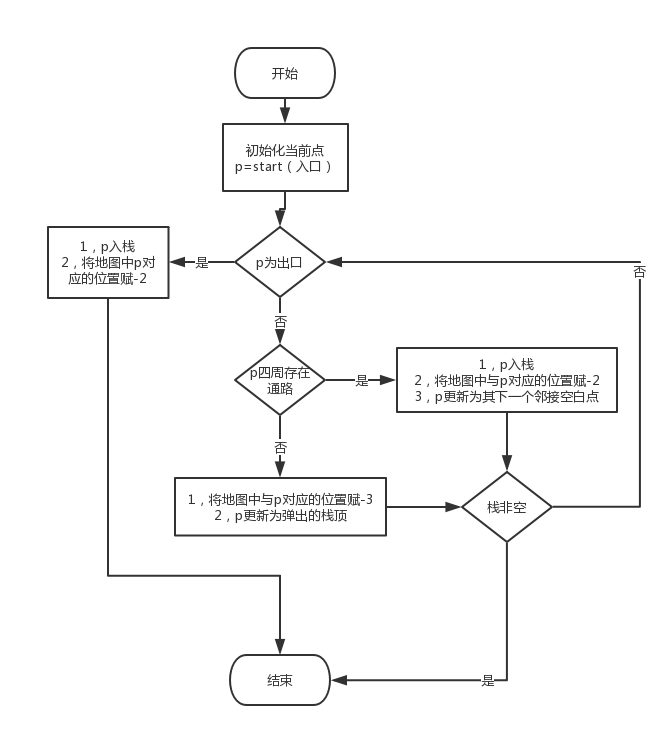
-1表示牆;0表示通路;-2表示已走過;-3表示此路不通;
1,假設最初以出發點為當前點p
2,判斷p是否為出口,
2.1若p為出口,p入棧,並在地圖相應位置賦-2,表示已經過,然後結束;
2.2若p不為出口,判斷p是否有空白鄰接點,
2.2.1若有,p入棧,在地圖相應位置賦-2,同時p更新為下一個空白鄰接點;
2.2.2若無,在p對應的地圖位置上賦-3,同時彈出棧頂作為p
3,棧非空,重複步驟2
資料結構
棧的資料結構我就不貼了,想看可以翻我部落格,有具體實現,這裡就直接用STL的棧啦
typedef struct
{
int x,y;
}Pos;//點x,y座標
typedef struct
{
int n;//迷宮大小
Pos start,end;//起止座標
int maze[N][N]; //迷宮分佈圖。-1-->牆;0-->通路
}Maze;
1 建迷宮咯
打死我我也不用檔案讀取資料,嘿嘿嘿,真香
//從檔案讀取迷宮
void CreateMaze(Maze &m)
{
fstream inFile("迷宮.txt",ios: 檔案迷宮.txt內容
10
1 4
1 8
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 0 0 -1 0 0 0 -1 0 -1
-1 0 0 -1 0 0 0 -1 0 -1
-1 0 0 0 0 -1 -1 0 0 -1
-1 0 -1 -1 -1 0 0 0 0 -1
-1 0 0 0 -1 0 0 0 0 -1
-1 0 -1 0 0 0 -1 0 0 -1
-1 0 -1 -1 -1 0 -1 -1 0 -1
-1 -1 0 0 0 0 0 0 0 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1
2 查通路呀
看看流程圖是不是發現是否存在通路這個判斷位於邏輯中心,沒有他真滴啥都做不了了呢,於是我們專門為他建立了一個函式,以示尊敬,希望他保佑我別出Bug
- 查詢通路按照我的習慣是東南西北順時針查詢,一找到立刻返回;但由於矩陣是x朝下,y朝右,所以大家寫的時候注意下x,y的處理;其實只要你囊括了四個方向,順序無所謂,最後都能達到目標,這裡只是個人編碼習慣問題
我希望它做兩件事,一是有通路返回最先找到的鄰接點;二是無通路返回(-1,-1)表示無通路
//-2->已走過;-3->不通
//判斷當前點是否存在通路,通,返回第一個可通的座標;不通,返回(-1,-1)
Pos Pass(Maze m,Pos curpos)
{
Pos nextpos;
//初始化表示無通路
nextpos.x = -1;
nextpos.y = -1;
int x,y;
x = curpos.x;
y = curpos.y;
//每次都按順序查詢,走過的路被標記為 -2,所以不會再走
//按照我們人的東西南北為參照,二維陣列x朝下,y朝右,所以應注意方向
if(m.maze[x][y+1] == 0)//東
{
nextpos.x = x;
nextpos.y = y+1;
}
else if(m.maze[x+1][y] == 0)//南
{
nextpos.x = x+1;
nextpos.y = y;
}
else if(m.maze[x][y-1] == 0)//西
{
nextpos.x = x;
nextpos.y = y-1;
}else if(m.maze[x-1][y] == 0)//北
{
nextpos.x = x-1;
nextpos.y = y;
}
return nextpos;
}
3 找活路啦
看著流程圖敲一敲,機智的你肯定沒問題啦
程式碼後半部分僅僅是為列印時的美觀,不寫也行,不過人家看臉啦,還是比較注重形式的呀,看著可舒服啦。處理也很簡單,再開一個棧(反正是STL他們家的,又不要錢)把從路徑棧中彈出的點壓入新棧,這樣順序就負負得正啦。然後把編號賦給彈出的棧頂在地圖中對應的位置。然後輸出地圖時令值大於0的輸出相應數值,其餘皆輸出#。這也是我為啥讓-2,-3表示走過的路,不同的路,因為他們大於0,阻擋了我最求美的道路,於是無情地將他們打入負數的冷宮
void MazePath(Maze m)
{
Pos curpos,nextpos;//當前位置,下個位置
stack<Pos> path_stack;//路徑棧
curpos = m.start;
do{
nextpos = Pass(m,curpos);
//超級大bug,當終點為當前點且其四周都被沒空白時,當前的的下一個點自然返回空,表示不可通,也就找不到終點了
//所以應該先判斷當前點是否為終點,是的話立刻退出,否則判斷是否存在通路,存在當前點就入棧;否則將當前置為-3,彈出棧頂作為當前點
if(curpos.x == m.end.x && curpos.y == m.end.y)//當前點為終點
{
path_stack.push(curpos);//當前點入路徑棧
m.maze[curpos.x][curpos.y] = -2;//走過標記為-2
break;
}
if(nextpos.x != -1)//表示可通
{
path_stack.push(curpos);//當前點入路徑棧
m.maze[curpos.x][curpos.y] = -2;//更新迷宮地圖,表示該點已經過
curpos = nextpos;//當前點更新為下一個點
}
else
{
m.maze[curpos.x][curpos.y] = -3;//表示當前點不通
curpos = path_stack.top();//當前點更新為棧頂元素
path_stack.pop();//刪除棧頂
}
}while(!path_stack.empty());
//=================以下僅僅是為了展示效果(人家看臉嘛)=======================
if(path_stack.empty())cout<<"死路一條!"<<endl;
else
{
stack<Pos>tmp_stack;
int ord = 0;
//被標記為1的不全是路徑上的點,但在棧中一定是路徑上的點
while(!path_stack.empty())
{
curpos = path_stack.top();
path_stack.pop();
tmp_stack.push(curpos);
}
while(!tmp_stack.empty())
{
ord++;
curpos = tmp_stack.top();
tmp_stack.pop();
m.maze[curpos.x][curpos.y] = ord;
}
//列印輸出
cout<<endl;
for(int i = 0; i < m.n; i++)
{
for(int j = 0; j < m.n; j++)
{
if(m.maze[i][j] > 0)
{
cout<<setw(2)<<m.maze[i][j]<<" ";
}
else cout<<setw(2)<<" # ";
}
cout<<endl;
}
}
}
說說心裡話
-
到這裡我的分享快到尾聲啦,我知道自己講得很糟糕,但是我會努力的,總有一天我也會變得像你一樣強
-
主體邏輯一定要清晰,這次一開始將當前點是否存在通路作為第一個判斷條件,在某些點作為出口時是得不出答案的,因為存在一種情況,當前點確實為終點,但是他舉目四望,發現走投無路啦,誰知,路就在他腳下,可他沒機會低頭就被丟向無路可走的深淵,只要他肯低頭,立馬就踏破鐵鞋無覓處,這告訴我們要腳踏實地,過好當下呀。好在我知錯就改,立刻將是否為終點作為第一判斷條件,避免了慘劇發生,不過還是付出些許代價的
-
今天收穫不小,關鍵是賊有成就感,對棧的理解有深了一步,有句話說得好,紙上得來終覺淺,覺知此事要躬行吶。
-
書看再多,不實踐,難以內化;實踐再多,不總結,難以深化;總結再多,不寫下來,難以昇華;寫得再多,你不點贊,難以開心
好啦,好啦,別依依不捨啦(我知道不會有人不捨),咳咳,我要回去畫電路圖啦,小夥伴們,回見,不要太想我哦
完整Code
#include<iostream>
using namespace std;
#include<stdlib.h>
#include<stack>
#include<fstream>
#include<iomanip>
#define N 20
typedef struct
{
int x,y;
}Pos;//x,y座標
typedef struct
{
int n;//迷宮大小
Pos start,end;//起止座標
int maze[N][N]; //迷宮分佈圖。-1-->牆;0-->通路
}Maze;
//從檔案讀取迷宮
void CreateMaze(Maze &m)
{
fstream inFile("迷宮.txt",ios::in);
if(!inFile)cout<<"檔案開啟失敗!"<<endl;
inFile>>m.n;
inFile>>m.start.x>>m.start.y;
inFile>>m.end.x>>m.end.y;
for(int i = 0; i < m.n; i++)
{
for(int j = 0; j < m.n; j++)
{
inFile>>m.maze[i][j];
}
}
inFile.close();
cout<<m.n<<endl;
cout<<m.start.x<<m.start.y<<endl;
cout<<m.end.x<<m.end.y<<endl;
for(int i = 0; i < m.n; i++)
{
for(int j = 0; j < m.n; j++)
{
cout<<m.maze[i][j]<<" ";
}
cout<<endl;
}
}
//-2->已走過;-3->不通
//判斷當前點是否存在通路,通,返回第一個可通的座標;不通,返回(-1,-1)
Pos Pass(Maze m,Pos curpos)
{
Pos nextpos;
//初始化表示無通路
nextpos.x = -1;
nextpos.y = -1;
int x,y;
x = curpos.x;
y = curpos.y;
//每次都按順序查詢,走過的路被標記為 1,所以不會再走
//按照我們人的東西南北為參照,二維陣列x朝下,y朝右,所以應注意方向
if(m.maze[x][y+1] == 0)//東
{
nextpos.x = x;
nextpos.y = y+1;
}
else if(m.maze[x+1][y] == 0)//南
{
nextpos.x = x+1;
nextpos.y = y;
}
else if(m.maze[x][y-1] == 0)//西
{
nextpos.x = x;
nextpos.y = y-1;
}else if(m.maze[x-1][y] == 0)//北
{
nextpos.x = x-1;
nextpos.y = y;
}
return nextpos;
}
void MazePath(Maze m)
{
Pos curpos,nextpos;//當前位置,下個位置
stack<Pos> path_stack;//路徑棧
curpos = m.start;//cout<<m.end.x<<m.end.y;
do{//cout<<"curpos: "<<curpos.x<<" "<<curpos.y<<endl;
nextpos = Pass(m,curpos); //cout<<"nextpos: "<<nextpos.x<<" "<<nextpos.y<<endl;
//超級大bug,當終點為當前點且其四周都被沒空白時,當前的的下一個點自然返回空,表示不可通,也就找不到終點了
//所以應該先判斷當前點是否為終點,是的話立刻退出,否則判斷是否存在通路,存在當前點就入棧;否則將當前置為-3,彈出棧頂作為當前點
if(curpos.x == m.end.x && curpos.y == m.end.y)//當前點為終點
{
path_stack.push(curpos);//當前點入路徑棧
m.maze[curpos.x][curpos.y] = -2;//走過標記為-2
break;
}
if(nextpos.x != -1)//表示可通
{
path_stack.push(curpos);//當前點入路徑棧
m.maze[curpos.x][curpos.y] = -2;//更新迷宮地圖,表示該點已經過
curpos = nextpos;//當前點更新為下一個點
}
else
{
m.maze[curpos.x][curpos.y] = -3;//表示當前點不通
curpos = path_stack.top();//當前點更新為棧頂元素
path_stack.pop();//刪除棧頂
}
}while(!path_stack.empty());
//以下僅僅是為了展示而處理效果
if(path_stack.empty())cout<<"死路一條!"<<endl;
else
{
stack<Pos>tmp_stack;
int ord = 0;
//被標記為1的不全是路徑上的點,但在棧中一定是路徑上的點
while(!path_stack.empty())
{
curpos = path_stack.top();
path_stack.pop();
tmp_stack.push(curpos);
// m.maze[curpos.x][curpos.y] = 5;
}
while(!tmp_stack.empty())
{
ord++;
curpos = tmp_stack.top();
tmp_stack.pop();
// tmp_stack.push(curpos);
m.maze[curpos.x][curpos.y] = ord;
}
cout<<endl;
for(int i = 0; i < m.n; i++)
{
for(int j = 0; j < m.n; j++)
{
if(m.maze[i][j] > 0)
{
cout<<setw(2)<<m.maze[i][j]<<" ";
}
else cout<<setw(2)<<" # ";
}
cout<<endl;
}
}
}
int main()
{
Maze m;
CreateMaze(m);
for(int i = 0; i < 10; i++)//測試:以所有點為終點
{
for(int j = 0; j < 10; j++)
{
m.end.x = i;
m.end.y = j;
cout<<"i: "<<i<<" j: "<<j<<endl;
MazePath(m);
}
}
// MazePath(m);
return 0;
}
