PROBLEM

給出一棵n個節點的樹，我們每次隨機染黑一個葉子節點（可以重複染黑），操作無限次後，這棵樹的所有葉子節點必然全部會被染成黑色。
定義R為這棵樹不經過黑點的直徑，求使R第一次變小期望的步數。

前置知識：樹的直徑的性質、期望的線性性

如果一棵樹有多條直徑，當直徑長為偶數時，多條直徑必定交於一點，當直徑長為奇數時，多條直徑必定經過同一邊，這一點或一邊必定在每條直徑的中間。

證明：

不同的直徑必定至少相交於一點（否則這兩條直徑上的點的路徑必定能使直徑變長），因此所有直徑都相交於一點。

對於長度為偶數的直徑，這個點若不為一條直徑的中點，那麼從另一條路徑經過這個點再前往這條長度大於直徑一半的路徑，直徑就會變長。奇數同理。

因此我們根據這個中點或這個處於中間的邊，可以把所有直徑的兩端分入若干個集合。如果在染點後只剩下了一個集合，那麼直徑必定變小。相反，如果有任意兩個集合裡有點沒有被染黑，那麼直徑依舊不變（請結合圖理解）。

再考慮一下將一個點染黑的期望步數。如果總點數為n,還未染黑的點為m，那麼染黑這m個點中任意一個點的期望：

F=1+(n-m)/n*f

即1步直接染黑，或染到已經染黑的n-m個點中，再染。

解方程即可得到f=n/m。

解決了每染一個點的期望之後，這個問題就轉化成了染剩一個集合的期望。

首先我們考慮那些不在直徑上的葉子，它們染或不染都不會對答案造成影響，因此我們假定我們不用染它們，它們對答案的影響僅僅是對f中的n的貢獻。

推公式。列舉染到最後剩下的集合，設這個集合的大小為d，設所有在直徑上的葉子總數為d0，我們從0到d-1列舉這個集合最後被染了i個點，注意這個集合在直徑變小之前不可能被染完了，不可能列舉到d。因為這樣子剩下的集合就不是它。

公式：

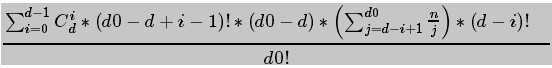
解釋：
從集合中d箇中選i個，有組合數C(d,i)。

染點有順序，共有(d0-d+i)個點要染，我們要保證最後一個不是這個集合裡的點，因提一個此先非該集合的點(d0-d)種出來，(d0-d+i-1)!，最後再把它放進去*(d0-d)。

從d0個點染到d-i個點，乘上貢獻。

最後因為在操作無線次後所有的點都被染了色，所以剩下d-i個點還有一個染色的順序。

最後除以總的方案數，也就是染點的順序。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define maxn 500005
#define mo 998244353
#define maxm 1000010
#define ll long long 
using namespace std;

int n,m,i,j,k,x,y,dx,dy,dlen;
int a[maxn],b[maxn],s[maxn];
int em,e[maxm],nx[maxm],ls[maxn],dep[maxn],fa[maxn],du[maxn];
ll jc[maxn],leaf,s0,ans,lassum[maxn],tmp;

void read(int &x){
	x=0; char ch=getchar();
	for(;ch<'0'||'9'<ch;ch=getchar());
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
}

void insert(int x,int y){
	em++; e[em]=y; nx[em]=ls[x]; ls[x]=em;
	em++; e[em]=x; nx[em]=ls[y]; ls[y]=em;
}

ll ksm(ll x,ll y){
	ll s=1;
	for(;y;y>>=1,x=x*x%mo) if (y&1)
		(s*=x)%=mo;
	return s;
}
ll C(ll n,ll m){return jc[n]*ksm(jc[n-m]*jc[m]%mo,mo-2)%mo;}
int dfs(int x,int p){
	dep[x]=dep[p]+1,fa[x]=p;
	int mxd1=0,mxd2=0;
	for(int i=ls[x];i;i=nx[i]) if (e[i]!=p){
		int tmp=dfs(e[i],x);
		if (dep[tmp]>dep[mxd1]) mxd2=mxd1,mxd1=tmp;
		else if (dep[tmp]>dep[mxd2]) mxd2=tmp;
	}
	if (mxd1&&mxd2&&dep[mxd1]+dep[mxd2]-dep[x]*2>dlen)
		dx=mxd1,dy=mxd2,dlen=dep[mxd1]+dep[mxd2]-dep[x]*2;
	if (mxd1&&dep[mxd1]-dep[x]>dlen)
		dx=x,dy=mxd1,dlen=dep[mxd1]-dep[x];
	if (!mxd1) return x; else return mxd1;
}

void getd(){
	x=dx,y=dy;
	if (dep[x]<dep[y]) swap(x,y);
	while (dep[x]>dep[y]) a[++a[0]]=x,x=fa[x];
	while (x!=y) a[++a[0]]=x,b[++b[0]]=y,x=fa[x],y=fa[y];
	a[++a[0]]=x;
	for(i=b[0];i>=1;i--) a[++a[0]]=b[i];
}


void dfs2(int x,int p,int tp){
	if (dep[x]==dlen/2) s[tp]++,s0++;
	for(int i=ls[x];i;i=nx[i]) if (e[i]!=p)
		dep[e[i]]=dep[x]+1,dfs2(e[i],x,tp);
}

int main(){
	freopen("winer.in","r",stdin);
	freopen("winer.out","w",stdout);
	read(n);
	for(i=1;i<n;i++){
		read(x),read(y);
		insert(x,y);
		du[x]++,du[y]++;
	}
	leaf=0; for(i=1;i<=n;i++) if (du[i]==1) leaf++;
	dfs(1,0);
	getd();
	if (dlen&1){
		x=a[a[0]/2],y=a[a[0]/2+1];
		s[0]=2;
		dep[x]=0,dfs2(x,y,1);
		dep[y]=0,dfs2(y,x,2);
	} else {
		x=a[a[0]/2+1];
		dep[x]=0;
		for(i=ls[x];i;i=nx[i]) dep[e[i]]=1,dfs2(e[i],x,++s[0]);
	}
	jc[0]=1,ans=0;
	for(i=1;i<=s0;i++) jc[i]=jc[i-1]*i%mo;
	for(i=s0;i>=1;i--) lassum[i]=(lassum[i+1]+leaf*ksm(i,mo-2)%mo)%mo;
	for(i=1;i<=s[0];i++) for(j=0;j<s[i];j++)
		(ans+=C(s[i],j)*jc[s0-s[i]+j-1]%mo*(s0-s[i])%mo*lassum[s[i]-j+1]%mo*jc[s[i]-j]%mo*ksm(jc[s0],mo-2)%mo)%=mo;
	printf("%lld",ans);
}