Deep Learning 8_深度學習UFLDL教程:Stacked Autocoders and Implement deep networks for digit classification_Exercise(斯坦福大學深度學習教程)
前言
2.實驗環境:win7, matlab2015b,16G記憶體,2T硬碟
3.實驗內容:Exercise: Implement deep networks for digit classification。利用深度網路完成MNIST手寫數字資料庫中手寫數字的識別。即:用6萬個已標註資料(即:6萬張28*28的影象塊(patches)),作為訓練資料集,然後把它輸入到棧式自編碼器中,它的第一層自編碼器提取出訓練資料集的一階特徵,接著把這個一階特徵輸入到第二層自編碼器中提取出二階特徵,然後把把這個二階特徵輸入到softmax分類器,再用原始資料的標籤和二階特徵來訓練softmax分類器,最後利用BP演算法對整個網路的權重值進行微調以更好地學習資料,再用1萬個已標註資料(即:1萬張28*28的影象塊(patches))作為測試資料集,用前面訓練好的softmax分類器對測試資料集進行分類,並計算分類的正確率。本節整個網路結構如下:
4.本節方法適用範圍
在什麼時候應用微調?通常僅在有大量已標註訓練資料的情況下使用。在這樣的情況下,微調能顯著提升分類器效能。然而,如果有大量未標註資料集(用於非監督特徵學習/預訓練),卻只有相對較少的已標註訓練集,微調的作用非常有限,這時可用Deep Learning七:Self-Taught Learning_Exercise(斯坦福大學深度學習教程UFLDL)中介紹的方法。
5.一些matlab函式
[params, netconfig] = stack2params(stack)
是將stack層次的網路引數(可能是多個引數)轉換成一個向量params,這樣有利用使用各種優化演算法來進行優化操作。Netconfig中儲存的是該網路的相關資訊,其中netconfig.inputsize表示的是網路的輸入層節點的個數。netconfig.layersizes中的元素分別表示每一個隱含層對應節點的個數。
[ cost, grad ] = stackedAECost(theta, inputSize, hiddenSize, numClasses, netconfig,lambda, data, labels)
該函式內部實現整個網路損失函式和損失函式對每個引數偏導的計算。其中損失函式是個實數值,當然就只有1個了,其計算方法是根據sofmax分類器來計算的,只需知道標籤值和softmax輸出層的值即可。而損失函式對所有引數的偏導卻有很多個,因此每個引數處應該就有一個偏導值,這些引數不僅包括了多個隱含層的,而且還包括了softmax那個網路層的。其中softmax那部分的偏導是根據其公式直接獲得,而深度網路層那部分這通過BP演算法方向推理得到(即先計算每一層的誤差值,然後利用該誤差值計算引數w和b)。
stack = params2stack(params, netconfig)
和上面的函式功能相反,是吧一個向量引數按照深度網路的結構依次展開。
[pred] = stackedAEPredict(theta, inputSize, hiddenSize, numClasses, netconfig, data)
這個函式其實就是對輸入的data資料進行預測,看該data對應的輸出類別是多少。其中theta為整個網路的引數(包括了分類器部分的網路),numClasses為所需分類的類別,netconfig為網路的結構引數。
[h, array] = display_network(A, opt_normalize, opt_graycolor, cols, opt_colmajor)
該函式是用來顯示矩陣A的,此時要求A中的每一列為一個權值,並且A是完全平方數。函式執行後會將A中每一列顯示為一個小的patch影象,具體的有多少個patch和patch之間該怎麼擺設是程式內部自動決定的。
struct:
s = sturct;表示建立一個結構陣列s。
nargout:
表示函式輸出引數的個數。
save:
比如函式save('saves/step2.mat', 'sae1OptTheta');則要求當前目錄下有saves這個目錄,否則該語句會呼叫失敗的。
棧式自編碼神經網路是一個由多層稀疏自編碼器組成的神經網路,其前一層自編碼器的輸出作為其後一層自編碼器的輸入。
6.解疑
在softmaxExercise.m中有如下一句程式碼:
images = loadMNISTImages('train-images.idx3-ubyte');
labels = loadMNISTLabels('train-labels.idx1-ubyte');
labels(labels==0) = 10; % 把標籤0變為標籤10,故labels的值是[1,10],而原來是[0,9] ?為什麼非要這樣?
為什麼非要把原來的標籤0變為標籤10呢?搞不懂!
這個問題在本節實驗中的stackedAEExercise.m中也有:
trainLabels(trainLabels == 0) = 10; % 一直沒搞懂,為什麼非要把標籤0變為10?
原因:為了方便後面預測分類結果時,能直接通過max函式返回的是大值的列號就是所預測的分類結果。如本節實驗中stackedAEPredict.m中的這句話:
[prob pred] = max(softmaxTheta*a{depth+1});
其中pred就是儲存的所要預測的結果。
7. 疑問
1.如果我們後面的分類器不是用的softmax分類器,而是用的其它的,比如svm等,這個時候前面特徵提取的網路引數已經預訓練好了,用該引數是可以初始化前面的網路,但是此時該怎麼微調呢?
2.從程式碼中,可以看出整個網路的代價函式實際上就是softmax分類器的代價函式,這是怎麼推導來的?
3.第二個隱含層的特徵怎麼顯示出來?這個問題折騰了我好幾天,然後最近還因為發一篇論文各種折騰,所以一直沒有靜下心來想這個問題。
為了解答這個問題,有必要把顯示每一層特徵的函式display_network.m完全看懂,搞懂為什麼不能按照用它顯示第一層特徵的方式來顯示第二特徵,所以在這裡我詳細註釋了display_network.m的程式碼,見下面。
首先,要清楚第二個隱含層特徵顯示不出來的原因是什麼,很多人(比如:Deep learning:二十四(stacked autoencoder練習))以為是這個原因: 因為display_network.m這個函式要求隱含層神經元數的均方根必須是整數,而在本節實驗中隱含層神經元數設定的是200,它不是一個整數的平方,所以不能顯示出來,但這只是一個程式編寫的問題,實際上這個問題很好解決,我們只需要把隱含層神經元數設定為196,就可以用按照顯示第一層特徵的方式用函式display_network.m把它顯示出。但實際上並不是這個原因,具體我們可以從下面得到的結果證明,結果如下:
隱含層神經元數設定為196時,第一層特徵視覺化為:

隱含層神經元數設定為196時,第二層特徵視覺化為:

從第二層特徵的視覺化結果可看出,上面實現第二層視覺化的方式肯定是錯的,因為它並沒有顯示出什麼點、角等特徵。
那麼,它究竟為什麼不能這樣顯示,究竟該怎麼樣顯示呢?這實際上是一個深度學習的一個研究方向,具體可參考:Deep Learning論文筆記之(七)深度網路高層特徵視覺化
8 代價函式
Ng沒有直接給出代價函式,但可能通過程式碼看出他的代價函式.他的計算代價函式的程式碼如下:
1 depth = size(stack, 1); % 隱藏層的數量 2 a = cell(depth+1, 1); % 輸入層和隱藏層的輸出值,即:輸入層的輸出值和隱藏層的啟用值 3 a{1} = data; % 輸入層的輸出值 4 Jweight = 0; % 權重懲罰項 5 m = size(data, 2); % 樣本數 6 7 % 計算隱藏層的啟用值 8 for i=2:numel(a) 9 a{i} = sigmoid(stack{i-1}.w*a{i-1}+repmat(stack{i-1}.b, [1 size(a{i-1}, 2)])); 10 %Jweight = Jweight + sum(sum(stack{i-1}.w).^2); 11 end 12 13 M = softmaxTheta*a{depth+1}; % a{depth+1}為最後一層隱藏層的輸出,此時M為輸入softmax層的資料,即它是未計算softmax層啟用函式前的數值. 14 M = bsxfun(@minus, M, max(M, [], 1)); %防止下一步計算指數函式時溢位 15 M = exp(M); 16 p = bsxfun(@rdivide, M, sum(M)); % p為softmax層的輸出,就是每種類別的分類概率 17 18 Jweight = Jweight + sum(softmaxTheta(:).^2); % softmaxTheta是softmax層的權重引數 19 20 % 計算softmax分類器的代價函式,為什麼它就是整個模型的代價函式? 21 cost = -1/m .* groundTruth(:)'*log(p(:)) + lambda/2*Jweight;% 代價函式=均方差項+權重衰減項(也叫:規則化項)
所以,其代價函式實際上就是softmax分類器的代價函式,而softmax的代價函式可見Softmax迴歸,即代價函式為:
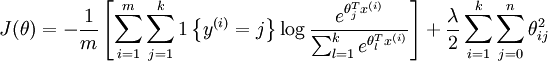
實驗步驟
1.初始化引數,載入MNIST手寫數字資料庫。
2.利用原始資料訓練第一個自編碼器,得到它的權重引數值sae1OptTheta,通過sae1OptTheta可得到原始資料的一階特徵sae1Features。
3.利用一階特徵sae1Features訓練第二個自編碼器,得到它的權重引數值sae2OptTheta,通過sae2OptTheta可得到原始資料的二階特徵sae2Features。
4.利用二階特徵sae2Features和原始資料的標籤來訓練softmax分類器,得到softmax分類器的權重引數saeSoftmaxOptTheta。
5.利用前面得到的所有權重引數sae1OptTheta、sae2OptTheta、saeSoftmaxOptTheta,得到微調前整個網路的權重引數stackedAETheta,然後在利用原始資料及其標籤的基礎上通過BP演算法對stackedAETheta進行微調,得到微調後的整個網路的權重引數stackedAEOptTheta。
6.通過微調前整個網路的權重引數stackedAETheta和微調後的整個網路的權重引數stackedAEOptTheta,分別對測試資料進行分類,得到兩者的分類準確率。
執行結果:
Before Finetuning Test Accuracy: 92.140%
After Finetuning Test Accuracy: 97.590%
第一層特徵顯示如下:

程式碼
stackedAEExercise.m:
%% CS294A/CS294W Stacked Autoencoder Exercise % Instructions % ------------ % % This file contains code that helps you get started on the % sstacked autoencoder exercise. You will need to complete code in % stackedAECost.m % You will also need to have implemented sparseAutoencoderCost.m and % softmaxCost.m from previous exercises. You will need the initializeParameters.m % loadMNISTImages.m, and loadMNISTLabels.m files from previous exercises. % % For the purpose of completing the assignment, you do not need to % change the code in this file. % %%====================================================================== %% STEP 0: Here we provide the relevant parameters values that will % allow your sparse autoencoder to get good filters; you do not need to % change the parameters below. DISPLAY = true; inputSize = 28 * 28; numClasses = 10; hiddenSizeL1 = 200; % Layer 1 Hidden Size hiddenSizeL2 = 200; % Layer 2 Hidden Size sparsityParam = 0.1; % desired average activation of the hidden units. % (This was denoted by the Greek alphabet rho, which looks like a lower-case "p", % in the lecture notes). lambda = 3e-3; % weight decay parameter beta = 3; % weight of sparsity penalty term %%====================================================================== %% STEP 1: Load data from the MNIST database % % This loads our training data from the MNIST database files. % Load MNIST database files trainData = loadMNISTImages('train-images.idx3-ubyte'); trainLabels = loadMNISTLabels('train-labels.idx1-ubyte'); trainLabels(trainLabels == 0) = 10; % 一直沒搞懂,為什麼非要把標籤0變為10? Remap 0 to 10 since our labels need to start from 1 %%====================================================================== %% STEP 2: Train the first sparse autoencoder % This trains the first sparse autoencoder on the unlabelled STL training % images. % If you've correctly implemented sparseAutoencoderCost.m, you don't need % to change anything here. % Randomly initialize the parameters sae1Theta = initializeParameters(hiddenSizeL1, inputSize); %% ---------------------- YOUR CODE HERE --------------------------------- % Instructions: Train the first layer sparse autoencoder, this layer has % an hidden size of "hiddenSizeL1" % You should store the optimal parameters in sae1OptTheta addpath minFunc/; options = struct; options.Method = 'lbfgs'; options.maxIter = 400; options.display = 'on'; [sae1OptTheta, cost] = minFunc(@(p)sparseAutoencoderCost(p,... inputSize,hiddenSizeL1,lambda,sparsityParam,beta,trainData),sae1Theta,options);%訓練出第一層網路的引數 save('saves/step2.mat', 'sae1OptTheta'); if DISPLAY W1 = reshape(sae1OptTheta(1:hiddenSizeL1 * inputSize), hiddenSizeL1, inputSize); display_network(W1'); end % ------------------------------------------------------------------------- %%====================================================================== %% STEP 3: Train the second sparse autoencoder % This trains the second sparse autoencoder on the first autoencoder % featurse. % If you've correctly implemented sparseAutoencoderCost.m, you don't need % to change anything here. % 利用第一個稀疏自編碼器的權重引數sae1OptTheta,得到輸入資料的一階特徵表示 [sae1Features] = feedForwardAutoencoder(sae1OptTheta, hiddenSizeL1, ... inputSize, trainData); % Randomly initialize the parameters sae2Theta = initializeParameters(hiddenSizeL2, hiddenSizeL1); %% ---------------------- YOUR CODE HERE --------------------------------- % Instructions: Train the second layer sparse autoencoder, this layer has % an hidden size of "hiddenSizeL2" and an inputsize of % "hiddenSizeL1" % % You should store the optimal parameters in sae2OptTheta [sae2OptTheta, cost] = minFunc(@(p)sparseAutoencoderCost(p,... hiddenSizeL1,hiddenSizeL2,lambda,sparsityParam,beta,sae1Features),sae2Theta,options);%訓練出第二層網路的引數 save('saves/step3.mat', 'sae2OptTheta'); figure; if DISPLAY W11 = reshape(sae1OptTheta(1:hiddenSizeL1 * inputSize), hiddenSizeL1, inputSize); W12 = reshape(sae2OptTheta(1:hiddenSizeL2 * hiddenSizeL1), hiddenSizeL2, hiddenSizeL1); % TODO(zellyn): figure out how to display a 2-level network % display_network(log(W11' ./ (1-W11')) * W12'); % W12_temp = W12(1:196,1:196); % display_network(W12_temp'); % figure; % display_network(W12_temp'); end % ------------------------------------------------------------------------- %%====================================================================== %% STEP 4: 用二階特徵訓練softmax分類器 Train the softmax classifier % This trains the sparse autoencoder on the second autoencoder features. % If you've correctly implemented softmaxCost.m, you don't need % to change anything here. % 利用第二個稀疏自編碼器的權重引數sae2OptTheta,得到輸入資料的二階特徵表示 [sae2Features] = feedForwardAutoencoder(sae2OptTheta, hiddenSizeL2, ... hiddenSizeL1, sae1Features); % Randomly initialize the parameters saeSoftmaxTheta = 0.005 * randn(hiddenSizeL2 * numClasses, 1);%這個引數拿來幹嘛?計算softmaxCost函式嗎?可以捨去! %因為softmaxCost函式在softmaxExercise練習中已經實現,並且已經證明其梯度計算是正確的! %% ---------------------- YOUR CODE HERE --------------------------------- % Instructions: Train the softmax classifier, the classifier takes in % input of dimension "hiddenSizeL2" corresponding to the % hidden layer size of the 2nd layer. % % You should store the optimal parameters in saeSoftmaxOptTheta % % NOTE: If you used softmaxTrain to complete this part of the exercise, % set saeSoftmaxOptTheta = softmaxModel.optTheta(:); softmaxLambda = 1e-4; numClasses = 10; softoptions = struct; softoptions.maxIter = 400; softmaxModel = softmaxTrain(hiddenSizeL2,numClasses,softmaxLambda,... sae2Features,trainLabels,softoptions); saeSoftmaxOptTheta = softmaxModel.optTheta(:);%得到softmax分類器的權重引數 save('saves/step4.mat', 'saeSoftmaxOptTheta'); % ------------------------------------------------------------------------- %%====================================================================== %% STEP 5: 微調 Finetune softmax model % Implement the stackedAECost to give the combined cost of the whole model % then run this cell. % Initialize the stack using the parameters learned stack = cell(2,1); stack{1}.w = reshape(sae1OptTheta(1:hiddenSizeL1*inputSize), ... hiddenSizeL1, inputSize); stack{1}.b = sae1OptTheta(2*hiddenSizeL1*inputSize+1:2*hiddenSizeL1*inputSize+hiddenSizeL1); stack{2}.w = reshape(sae2OptTheta(1:hiddenSizeL2*hiddenSizeL1), ... hiddenSizeL2, hiddenSizeL1); stack{2}.b = sae2OptTheta(2*hiddenSizeL2*hiddenSizeL1+1:2*hiddenSizeL2*hiddenSizeL1+hiddenSizeL2); % Initialize the parameters for the deep model [stackparams, netconfig] = stack2params(stack);%把stack層(即:兩個隱藏層)的權重引數變為一個向量stackparams stackedAETheta = [ saeSoftmaxOptTheta ; stackparams ];% 得到微調前整個網路引數向量stackedAETheta,它包括softmax分類器那部分的引數向量saeSoftmaxOptTheta,且分類器那部分的引數放前面 %% ---------------------- YOUR CODE HERE --------------------------------- % Instructions: Train the deep network, hidden size here refers to the ' % dimension of the input to the classifier, which corresponds % to "hiddenSizeL2". % % 用BP演算法微調,得到微調後的整個網路引數stackedAEOptTheta [stackedAEOptTheta, cost] = minFunc(@(p)stackedAECost(p,inputSize,hiddenSizeL2,... numClasses, netconfig,lambda, trainData, trainLabels),... stackedAETheta,options);%訓練出第三層網路的引數 save('saves/step5.mat', 'stackedAEOptTheta'); figure; if DISPLAY optStack = params2stack(stackedAEOptTheta(hiddenSizeL2*numClasses+1:end), netconfig); W11 = optStack{1}.w; W12 = optStack{2}.w; % TODO(zellyn): figure out how to display a 2-level network % display_network(log(1 ./ (1-W11')) * W12'); end % ------------------------------------------------------------------------- %%====================================================================== %% STEP 6: Test % Instructions: You will need to complete the code in stackedAEPredict.m % before running this part of the code % % Get labelled test images % Note that we apply the same kind of preprocessing as the training set testData = loadMNISTImages('t10k-images.idx3-ubyte'); testLabels = loadMNISTLabels('t10k-labels.idx1-ubyte'); testLabels(testLabels == 0) = 10; % Remap 0 to 10 [pred] = stackedAEPredict(stackedAETheta, inputSize, hiddenSizeL2, ... numClasses, netconfig, testData); acc = mean(testLabels(:) == pred(:)); fprintf('Before Finetuning Test Accuracy: %0.3f%%\n', acc * 100); [pred] = stackedAEPredict(stackedAEOptTheta, inputSize, hiddenSizeL2, ... numClasses, netconfig, testData); acc = mean(testLabels(:) == pred(:)); fprintf('After Finetuning Test Accuracy: %0.3f%%\n', acc * 100); % Accuracy is the proportion of correctly classified images % The results for our implementation were: % % Before Finetuning Test Accuracy: 87.7% % After Finetuning Test Accuracy: 97.6% % % If your values are too low (accuracy less than 95%), you should check % your code for errors, and make sure you are training on the % entire data set of 60000 28x28 training images % (unless you modified the loading code, this should be the case)
stackedAECost.m
1 function [ cost, grad ] = stackedAECost(theta, inputSize, hiddenSize, ... 2 numClasses, netconfig, ... 3 lambda, data, labels) 4 % 計算整個模型的代價函式及其梯度 5 % 注意:完成這個函式後最好用checkStackedAECost函式檢查梯度計算是否正確 6 7 % stackedAECost: Takes a trained softmaxTheta and a training data set with labels, 8 % and returns cost and gradient using a stacked autoencoder model. Used for 9 % finetuning. 10 11 % theta: trained weights from the autoencoder 12 % visibleSize: the number of input units 13 % hiddenSize: the number of hidden units *at the 2nd layer* 14 % numClasses: the number of categories 15 % netconfig: the network configuration of the stack 16 % lambda: the weight regularization penalty 17 % data: Our matrix containing the training data as columns. So, data(:,i) is the i-th training example. 18 % labels: A vector containing labels, where labels(i) is the label for the 19 % i-th training example 20 21 22 %% Unroll softmaxTheta parameter 23 24 % We first extract the part which compute the softmax gradient 25 softmaxTheta = reshape(theta(1:hiddenSize*numClasses), numClasses, hiddenSize);%從整個網路引數向量中提取出softmax分類器部分的引數,並以矩陣表示 26 27 % Extract out the "stack" 28 stack = params2stack(theta(hiddenSize*numClasses+1:end), netconfig);%從整個網路引數向量中提取出隱藏層部分的引數,並以結構表示 29 30 % You will need to compute the following gradients 31 softmaxThetaGrad = zeros(size(softmaxTheta));% softmaxTheta的梯度 32 stackgrad = cell(size(stack)); % stack的梯度 33 for d = 1:numel(stack) 34 stackgrad{d}.w = zeros(size(stack{d}.w)); 35 stackgrad{d}.b = zeros(size(stack{d}.b)); 36 end 37 38 cost = 0; % You need to compute this 39 40 % You might find these variables useful 41 M = size(data, 2); 42 groundTruth = full(sparse(labels, 1:M, 1)); 43 44 45 %% --------------------------- YOUR CODE HERE ----------------------------- 46 % Instructions: Compute the cost function and gradient vector for 47 % the stacked autoencoder. 48 % 49 % You are given a stack variable which is a cell-array of 50 % the weights and biases for every layer. In particular, you 51 % can refer to the weights of Layer d, using stack{d}.w and 52 % the biases using stack{d}.b . To get the total number of 53 % layers, you can use numel(stack). 54 % 55 % The last layer of the network is connected to the softmax 56 % classification layer, softmaxTheta. 57 % 58 % You should compute the gradients for the softmaxTheta, 59 % storing that in softmaxThetaGrad. Similarly, you should 60 % compute the gradients for each layer in the stack, storing 61 % the gradients in stackgrad{d}.w and stackgrad{d}.b 62 % Note that the size of the matrices in stackgrad should 63 % match exactly that of the size of the matrices in stack. 64 % 65 66 depth = size(stack, 1); % 隱藏層的數量 67 a = cell(depth+1, 1); % 輸入層和隱藏層的輸出值,即:輸入層的輸出值和隱藏層的啟用值 68 a{1} = data; % 輸入層的輸出值 69 Jweight = 0; % 權重懲罰項 70 m = size(data, 2); % 樣本數 71 72 % 計算隱藏層的啟用值 73 for i=2:numel(a) 74 a{i} = sigmoid(stack{i-1}.w*a{i-1}+repmat(stack{i-1}.b, [1 size(a{i-1}, 2)])); 75 %Jweight = Jweight + sum(sum(stack{i-1}.w).^2); 76 end 77 78 M = softmaxTheta*a{depth+1}; 79 M = bsxfun(@minus, M, max(M, [], 1)); %防止下一步計算指數函式時溢位 80 M = exp(M); 81 p = bsxfun(@rdivide, M, sum(M)); 82 83 Jweight = Jweight + sum(softmaxTheta(:).^2); 84 85 % 計算softmax分類器的代價函式,為什麼它就是整個模型的代價函式? 86 cost = -1/m .* groundTruth(:)'*log(p(:)) + lambda/2*Jweight;% 代價函式=均方差項+權重衰減項(也叫:規則化項) 87 88 %計算softmax分類器代價函式的梯度,即輸出層的梯度 89 softmaxThetaGrad = -1/m .* (groundTruth - p)*a{depth+1}' + lambda*softmaxTheta; 90 91 delta = cell(depth+1, 1); %隱藏層和輸出層的殘差 92 93 %計算輸出層的殘差 94 delta{depth+1} = -softmaxTheta' * (groundTruth - p) .* a{depth+1} .* (1-a{depth+1}); 95 96 %計算隱藏層的殘差 97 for i=depth:-1:2 98 delta{i} = stack{i}.w'*delta{i+1}.*a{i}.*(1-a{i}); 99 end 100 101 % 通過前面得到的輸出層和隱藏層的殘差,計算隱藏層引數的梯度 102 for i=depth:-1:1 103 stackgrad{i}.w = 1/m .* delta{i+1}*a{i}'; 104 stackgrad{i}.b = 1/m .* sum(delta{i+1}, 2); 105 end 106 107 % ------------------------------------------------------------------------- 108 109 %% Roll gradient vector 110 grad = [softmaxThetaGrad(:) ; stack2params(stackgrad)]; 111 112 end 113 114 115 % You might find this useful 116 function sigm = sigmoid(x) 117 sigm = 1 ./ (1 + exp(-x)); 118 end
stackedAEPredict.m
1 function [pred] = stackedAEPredict(theta, inputSize, hiddenSize, numClasses, netconfig, data) 2 3 % stackedAEPredict: Takes a trained theta and a test data set, 4 % and returns the predicted labels for each example. 5 6 % theta: trained weights from the autoencoder 7 % visibleSize: the number of input units 8 % hiddenSize: the number of hidden units *at the 2nd layer* 9 % numClasses: the number of categories 10 % data: Our matrix containing the training data as columns. So, data(:,i) is the i-th training example. 11 12 % Your code should produce the prediction matrix 13 % pred, where pred(i) is argmax_c P(y(c) | x(i)). 14 15 %% Unroll theta parameter 16 17 % We first extract the part which compute the softmax gradient 18 softmaxTheta = reshape(theta(1:hiddenSize*numClasses), numClasses, hiddenSize); 19 20 % Extract out the "stack" 21 stack = params2stack(theta(hiddenSize*numClasses+1:end), netconfig); 22 23 %% ---------- YOUR CODE HERE -------------------------------------- 24 % Instructions: Compute pred using theta assuming that the labels start 25 % from 1. 26 27 depth = numel(stack); 28 a = cell(depth+1); 29 a{1} = data; 30 m = size(data, 2); 31 32 for i=2:depth+1 33 a{i} = sigmoid(stack{i-1}.w*a{i-1}+ repmat(stack{i-1}.b, [1 m])); 34 end 35 36 [prob pred] = max(softmaxTheta*a{depth+1}); 37 38 39 40 41 % ----------------------------------------------------------- 42 43 end 44 45 46 % You might find this useful 47 function sigm = sigmoid(x) 48 sigm = 1 ./ (1 + exp(-x)); 49 end
display_network.m
1 function [h, array] = display_network(A, opt_normalize, opt_graycolor, cols, opt_colmajor) 2 % This function visualizes filters in matrix A. Each column of A is a 3 % filter. We will reshape each column into a square image and visualizes 4 % on each cell of the visualization panel. 5 % All other parameters are optional, usually you do not need to worry 6 % about it. 7 % opt_normalize:whether we need to normalize the filter so that all of 8 % them can have similar contrast. Default value is true. 9 % opt_graycolor: whether we use gray as the heat map. Default is true. 10 % cols: how many columns are there in the display. Default value is the 11 % squareroot of the number of columns in A. 12 % opt_colmajor: you can switch convention to row major for A. In that 13 % case, each row of A is a filter. Default value is false. 14 15 % opt_normalize:是否需要歸一化的引數。真:每個影象塊歸一化(即:每個影象塊元素值除以該影象塊中畫素值絕對值的最大值); 16 % 假:整幅大影象一起歸一化(即:每個影象塊元素值除以整幅影象中畫素值絕對值的最大值)。預設為真。 17 % opt_graycolor: 該引數決定是否顯示灰度圖。 18 % 真:顯示灰度圖;假:不顯示灰度圖。預設為真。 19 % cols: 該引數決定將要顯示的整幅大影象每一行中小影象塊的個數。預設為A列數的均方根。 20 % opt_colmajor:該引數決定將要顯示的整個大影象中每個小影象塊是按行從左到右依次排列,還是按列從上到下依次排列 21 % 真:整個大影象由每個小影象塊按列從上到下依次排列組成; 22 % 假:整個大影象由每個小影象塊按行從左到右依次排列組成。預設為假。 23 24 warning off all %關閉警告 25 26 % 引數的預設值 27 if ~exist('opt_normalize', 'var') || isempty(opt_normalize) 28 opt_normalize= true; 29 end 30 31 if ~exist('opt_graycolor', 'var') || isempty(opt_graycolor) 32 opt_graycolor= true; 33相關推薦
Deep Learning 8_深度學習UFLDL教程:Stacked Autocoders and Implement deep networks for digit classification_Exercise(斯坦福大學深度學習教程)
前言 2.實驗環境:win7, matlab2015b,16G記憶體,2T硬碟 3.實驗內容:Exercise: Implement deep networks for digit classification。利用深度網路完成MNIST手寫數字資料庫中手寫數字的識別。即:用6萬個已標註資料(即:6萬
Deep Learning 1_深度學習UFLDL教程:Sparse Autoencoder練習(斯坦福大學深度學習教程)
1前言 本人寫技術部落格的目的,其實是感覺好多東西,很長一段時間不動就會忘記了,為了加深學習記憶以及方便以後可能忘記後能很快回憶起自己曾經學過的東西。 首先,在網上找了一些資料,看見介紹說UFLDL很不錯,很適合從基礎開始學習,Adrew Ng大牛寫得一點都不裝B,感覺非常好
Deep Learning 4_深度學習UFLDL教程:PCA in 2D_Exercise(斯坦福大學深度學習教程)
前言 本節練習的主要內容:PCA,PCA Whitening以及ZCA Whitening在2D資料上的使用,2D的資料集是45個數據點,每個資料點是2維的。要注意區別比較二維資料與二維影象的不同,特別是在程式碼中,可以看出主要二維資料的在PCA前的預處理不需要先0均值歸一化,而二維自然影象需要先
Deep Learning 3_深度學習UFLDL教程:預處理之主成分分析與白化_總結(斯坦福大學深度學習教程)
1PCA ①PCA的作用:一是降維;二是可用於資料視覺化; 注意:降維的原因是因為原始資料太大,希望提高訓練速度但又不希望產生很大的誤差。 ② PCA的使用場合:一是希望提高訓練速度;二是記憶體太小;三是希望資料視覺化。 ③用PCA前的預處理:(1)規整化特徵的均值大致為0;(
Deep Learning 19_深度學習UFLDL教程:Convolutional Neural Network_Exercise(斯坦福大學深度學習教程)
基礎知識 概述 CNN是由一個或多個卷積層(其後常跟一個下采樣層)和一個或多個全連線層組成的多層神經網路。CNN的輸入是2維影象(或者其他2維輸入,如語音訊號)。它通過區域性連線和權值共享,再通過池化可得到平移不變特徵。CNN的另一個優點就是易於訓練
Deep Learning 11_深度學習UFLDL教程:資料預處理(斯坦福大學深度學習教程)
資料預處理是深度學習中非常重要的一步!如果說原始資料的獲得,是深度學習中最重要的一步,那麼獲得原始資料之後對它的預處理更是重要的一部分。 1.資料預處理的方法: ①資料歸一化: 簡單縮放:對資料的每一個維度的值進行重新調節,使其在 [0,1]或[ − 1,1] 的區間內 逐樣本均值消減:在每個
Deep Learning 13_深度學習UFLDL教程:Independent Component Analysis_Exercise(斯坦福大學深度學習教程)
前言 實驗環境:win7, matlab2015b,16G記憶體,2T機械硬碟 難點:本實驗難點在於執行時間比較長,跑一次都快一天了,並且我還要驗證各種代價函式的對錯,所以跑了很多次。 實驗基礎說明: ①不同點:本節實驗中的基是標準正交的,也是線性獨立的,而Deep Learni
Deep Learning 12_深度學習UFLDL教程:Sparse Coding_exercise(斯坦福大學深度學習教程)
前言 實驗環境:win7, matlab2015b,16G記憶體,2T機械硬碟 本節實驗比較不好理解也不好做,我看很多人最後也沒得出好的結果,所以得花時間仔細理解才行。 實驗內容:Exercise:Sparse Coding。從10張512*512的已經白化後的灰度影象(即:Deep Learnin
Deep Learning 6_深度學習UFLDL教程:Softmax Regression_Exercise(斯坦福大學深度學習教程)
前言 練習內容:Exercise:Softmax Regression。完成MNIST手寫數字資料庫中手寫數字的識別,即:用6萬個已標註資料(即:6萬張28*28的影象塊(patches)),作訓練資料集,然後利用其訓練softmax分類器,再用1萬個已標註資料(即:1萬張28*28的影象塊(pa
Deep Learning 7_深度學習UFLDL教程:Self-Taught Learning_Exercise(斯坦福大學深度學習教程)
前言 理論知識:自我學習 練習環境:win7, matlab2015b,16G記憶體,2T硬碟 一是用29404個無標註資料unlabeledData(手寫數字資料庫MNIST Dataset中數字為5-9的資料)來訓練稀疏自動編碼器,得到其權重引數opttheta。這一步的目的是提取這
Deep Learning 2_深度學習UFLDL教程:向量化程式設計(斯坦福大學深度學習教程)
1前言 本節主要是讓人用向量化程式設計代替效率比較低的for迴圈。 在前一節的Sparse Autoencoder練習中已經實現了向量化程式設計,所以與前一節的區別只在於本節訓練集是用MINIST資料集,而上一節訓練集用的是從10張圖片中隨機選擇的8*8的10000張小圖塊。綜上,只需要在
Deep Learning 9_深度學習UFLDL教程:linear decoder_exercise(斯坦福大學深度學習教程)
前言 實驗基礎說明: 1.為什麼要用線性解碼器,而不用前面用過的棧式自編碼器等?即:線性解碼器的作用? 這一點,Ng已經在講解中說明了,因為線性解碼器不用要求輸入資料範圍一定為(0,1),而前面用過的棧式自編碼器等要求輸入資料範圍必須為(0,1)。因為a3的輸出值是f函式的輸出,而在普通的spa
Deep Learning 10_深度學習UFLDL教程:Convolution and Pooling_exercise(斯坦福大學深度學習教程)
前言 實驗環境:win7, matlab2015b,16G記憶體,2T機械硬碟 實驗內容:Exercise:Convolution and Pooling。從2000張64*64的RGB圖片(它是 the STL10 Dataset的一個子集)中提取特徵作為訓練資料集,訓練softmax分類器,然後從
Deep Learning 5_深度學習UFLDL教程:PCA and Whitening_Exercise(斯坦福大學深度學習教程)
close all; % clear all; %%================================================================ %% Step 0a: Load data % Here we provide the code to load n
Joint Deep Learning For Pedestrian Detection(論文筆記-深度學習:行人檢測)
一、摘要: 行人檢測主要分為四部分:特徵提取、形變處理、遮擋處理和分類。現存方法都是四個部分獨立進行,本文聯合深度學習將四個部分結合在一起,最大化其能力。 二、引言
CS294-112深度增強學習課程(加州大學伯克利分校 2017)NO.3 Learning dynamical system models from data
增強 data learning http src img sys 增強學習 學習
斯坦福大學深度學習筆記:邏輯迴歸
z 邏輯迴歸(LOGISTIC REGRESSION) Logistic regression (邏輯迴歸)是當前業界比較常用的機器學習方法,用於估計某種事物的可能性。之前在經典之作《數學之美》中也看到了它用於廣告預測,也就是根據某廣告被使用者點選的可
斯坦福大學深度學習筆記:神經網路
神經網路演算法在八十到九十年代被廣泛使用過, 20世紀90年代,各種各樣的淺層機器學習模型相繼被提出,例如支撐向量機(SVM,Support Vector Machines)、 Boosting、最大熵方法(如LR,Logistic Regression)等。但之後便使用的變少了。但最近又開始流行起來了,原
Deep Learning 32: 自己寫的keras的一個callbacks函式,解決keras中不能在每個epoch實時顯示學習速率learning rate的問題
1 from __future__ import absolute_import 2 from . import backend as K 3 from .utils.generic_utils import get_from_module 4 from six.moves import z
分布式學習最佳實踐:從分布式系統的特征開始(附思維導圖)
擴展 問題 sca ref 調度 這也 集中 技術 park 我的探索歷程 這一部分,與分布式不大相關,記錄的是我是如何在分布式學習這條道路上摸索的,不感興趣的讀者請直接跳到下一章。 過去的一年,我在分布式學習這條道路上苦苦徘徊,始終沒有找到一個好的學

