Deep Learning 19_深度學習UFLDL教程:Convolutional Neural Network_Exercise(斯坦福大學深度學習教程)
基礎知識
概述
CNN是由一個或多個卷積層(其後常跟一個下采樣層)和一個或多個全連線層組成的多層神經網路。CNN的輸入是2維影象(或者其他2維輸入,如語音訊號)。它通過區域性連線和權值共享,再通過池化可得到平移不變特徵。CNN的另一個優點就是易於訓練,相比同樣隱含層單元的全連線網路,它需要訓練的引數個數要少得多。本文將介紹CNN的結構和後向傳播演算法,該演算法用於計算對模型引數的梯度。卷積和池化可看前面相應的教程。
結構
CNN由一些卷積層和下采樣層交替組成,也可視需要在最後加全連線層。一個卷積層的輸入是m*m*r的影象,其中m是影象的高度和寬度,r是通道數,如RGB影象的r=3。卷積層有k個濾波器(或核函式),大小為n*n*q,其中n小於影象的維數,q小於等於r且每個濾波器的q可能不一樣。濾波器的大小產生區域性連線結構,該結構是由每個濾波器與輸入影象卷積得到k個特徵圖,每個特徵圖大小為m-n+1。然後,每個特徵圖通過p*p連續區域的平均或最大池化的方式來子取樣,其中p一般取2(當輸入為小影象時,如MNIST)和5(當輸入是大影象時)之間。在子取樣層的前後均需對每個特徵圖加一個附加偏置項和sigmoid非線性變化。下圖顯示了一個由卷積層和子取樣層組成的CNN。其中,相同顏色的單元共享權值。
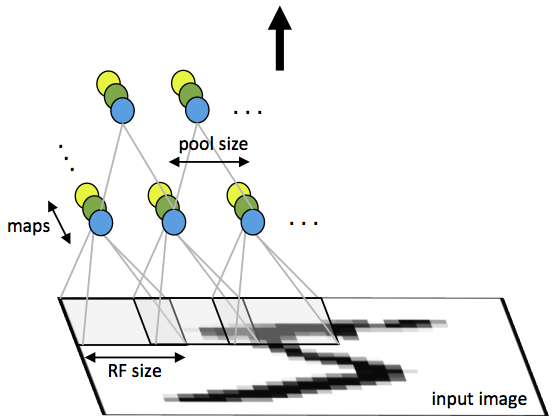
圖1.卷積神經網路的帶池化的第一層。相同顏色的神經元共享權值,不同顏色神經元表示不同的特徵圖。
在卷積層的最後可能會有一些全連線層。該層是與一個標準多層神經網路中的層是一樣的。
後向傳播
δ(l+1)中是l+1層的殘差,代價函式為J(W,b;x,y),其中(W,b)是引數,(x,y)分別是訓練資料和標籤。則l層的殘差和梯度分別為:
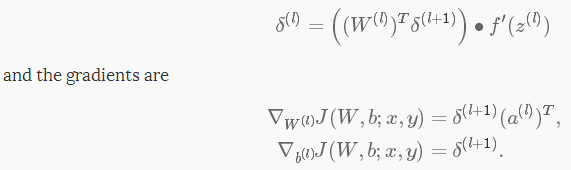
如果l層是一個卷積層和子取樣層,則其殘差為:

其中,k是濾波器個數, 是啟用函式的偏層數。通過計算傳入池化層每個神經元的殘差,子取樣必須通過池化層傳播殘差。
是啟用函式的偏層數。通過計算傳入池化層每個神經元的殘差,子取樣必須通過池化層傳播殘差。
最後,為了計算特徵圖的梯度,利用邊緣處理卷積運算得到殘差矩陣,再翻轉殘差矩陣。在卷積層翻轉濾波器和最後翻轉殘差矩陣效果是一樣的。
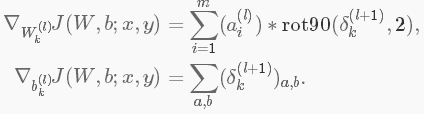
其中,
a(L)是L層的輸入,a(1)是輸入影象。 是一個合理的卷積運算,該卷積是第l層的第i個輸入與對第k個濾波器的殘差相卷。
是一個合理的卷積運算,該卷積是第l層的第i個輸入與對第k個濾波器的殘差相卷。
練習
練習內容:UFLDL:Exercise: Convolutional Neural Network。利用卷積神經網路實現數字分類。該神經網路有2層,第一層是卷積和子取樣層,第二層是全連線層。即:本節的網路結構為:一個卷積層+一個pooling層+一個softmax層。本節練習中,輸入影象為28*28,卷積核大小為9*9,卷積層特徵個數(即:卷積核個數)為20個,池化連續區域為2*2,輸出為類別為10類。
注意:本練習中的卷積核,並不是由自編碼器學習的特徵,而是隨機隨機始化所得
一些matlab函式
1.addpath
語法:
新增路徑:addpath('當前路徑中的資料夾名1','當前路徑下的資料夾名2','當前路徑中的資料夾名n');【即可一次性新增多個路徑】
addpath('./上級目錄中的資料夾1','./上級目錄中的資料夾2','./上級目錄中的資料夾n');
addpath('../更上一級目錄中的資料夾1','../更上一級目錄中的資料夾2','../更上一級目錄中的資料夾n');
3.sub2ind函式
ind2sub函式可以用來把矩陣元素的index轉換成對應的下標(determines the equivalent subscript values corresponding to a single index into an array)
例如: 一個4*5的矩陣A,第2行第2個元素的index的6(matlab中matrix是按列順序排列),可以用ind2sub函式來計算這個元素的下標 [I,J] = ind2sub(size(A),6)
4.sparse和full函式
下面這句話經常可見:
groundTruth = full(sparse(labels, 1:numImages, 1));
它得到的結果是這樣一個矩陣:在第i行第j列元素值為1,其他元素為0,其中,i是向量labels內的第k個元素值,j是向量1:numImages內的第k個元素值。
故,在cnnCost.m中計算cost的程式碼為:
logProbs = log(probs); labelIndex=sub2ind(size(logProbs), labels', 1:size(logProbs,2)); %找出矩陣logProbs的線性索引,行由labels指定,列由1:size(logProbs,2)指定,生成線性索引返回給labelIndex values = logProbs(labelIndex); cost = -sum(values); weightDecayCost = (weightDecay/2) * (sum(Wd(:) .^ 2) + sum(Wc(:) .^ 2)); cost = cost / numImages+weightDecayCost;
可把它替換為:
groundTruth = full(sparse(labels, 1:numImages, 1)); cost = -1./numImages*groundTruth(:)'*log(probs(:))+(weightDecay/2.)*(sum(Wd(:).^2)+sum(Wc(:).^2)); %加入一個懲罰項
變得效率更快,程式碼更簡潔。
練習步驟
STEP 1:實現CNN代價函式和梯度計算
STEP 1a: Forward Propagation
STEP 1b: Calculate Cost
代價函式:

其中,J(W,b)為:
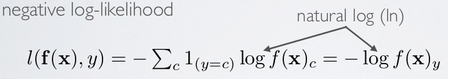
STEP 1c: Backpropagation
pool 層誤差:poolError,這一層首先根據公式δl = Wδl+1 * f'(zl)(pool層沒有f'(zl)這一項)計算該層的error。即poolError為:δl = Wδl+1
展開poolError為unpoolError,
convolution層誤差:convError,還是根據公式δl = Wδl+1 * f'(zl)來計算
STEP 1d: Gradient Calculation
Wd和bd的梯度計算公式:
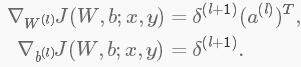
Step 2: Gradient Check
非常重要的一步
Step 3: Learn Parameters
在minFuncSGD中加上衝量的影響即可。
Step 4: Test
結果為:

程式碼
cnnTrain.m
%% Convolution Neural Network Exercise % Instructions % ------------ % % This file contains code that helps you get started in building a single. % layer convolutional nerual network. In this exercise, you will only % need to modify cnnCost.m and cnnminFuncSGD.m. You will not need to % modify this file. %%====================================================================== %% STEP 0: Initialize Parameters and Load Data % Here we initialize some parameters used for the exercise. % Configuration imageDim = 28; numClasses = 10; % Number of classes (MNIST images fall into 10 classes) filterDim = 9; % Filter size for conv layer,9*9 numFilters = 20; % Number of filters for conv layer poolDim = 2; % Pooling dimension, (should divide imageDim-filterDim+1) % Load MNIST Train addpath ../common/; images = loadMNISTImages('../common/train-images-idx3-ubyte'); images = reshape(images,imageDim,imageDim,[]); labels = loadMNISTLabels('../common/train-labels-idx1-ubyte'); labels(labels==0) = 10; % Remap 0 to 10 % Initialize Parameters,theta=(2165,1),2165=9*9*20+20+100*20*10+10 theta = cnnInitParams(imageDim,filterDim,numFilters,poolDim,numClasses); %%====================================================================== %% STEP 1: Implement convNet Objective % Implement the function cnnCost.m. %%====================================================================== %% STEP 2: Gradient Check % Use the file computeNumericalGradient.m to check the gradient % calculation for your cnnCost.m function. You may need to add the % appropriate path or copy the file to this directory. % DEBUG=false; % set this to true to check gradient DEBUG = true; if DEBUG % To speed up gradient checking, we will use a reduced network and % a debugging data set db_numFilters = 2; db_filterDim = 9; db_poolDim = 5; db_images = images(:,:,1:10); db_labels = labels(1:10); db_theta = cnnInitParams(imageDim,db_filterDim,db_numFilters,... db_poolDim,numClasses); [cost grad] = cnnCost(db_theta,db_images,db_labels,numClasses,... db_filterDim,db_numFilters,db_poolDim); % Check gradients numGrad = computeNumericalGradient( @(x) cnnCost(x,db_images,... db_labels,numClasses,db_filterDim,... db_numFilters,db_poolDim), db_theta); % Use this to visually compare the gradients side by side disp([numGrad grad]); diff = norm(numGrad-grad)/norm(numGrad+grad); % Should be small. In our implementation, these values are usually % less than 1e-9. disp(diff); assert(diff < 1e-9,... 'Difference too large. Check your gradient computation again'); end; %%====================================================================== %% STEP 3: Learn Parameters % Implement minFuncSGD.m, then train the model. % 因為是採用的mini-batch梯度下降法,所以總共對樣本的迴圈次數次數比標準梯度下降法要少 % 很多,因為每次迴圈中權值已經迭代多次了 options.epochs = 3; options.minibatch = 256; options.alpha = 1e-1; options.momentum = .95; opttheta = minFuncSGD(@(x,y,z) cnnCost(x,y,z,numClasses,filterDim,... numFilters,poolDim),theta,images,labels,options); save('theta.mat','opttheta'); %%====================================================================== %% STEP 4: Test % Test the performance of the trained model using the MNIST test set. Your % accuracy should be above 97% after 3 epochs of training testImages = loadMNISTImages('../common/t10k-images-idx3-ubyte'); testImages = reshape(testImages,imageDim,imageDim,[]); testLabels = loadMNISTLabels('../common/t10k-labels-idx1-ubyte'); testLabels(testLabels==0) = 10; % Remap 0 to 10 [~,cost,preds]=cnnCost(opttheta,testImages,testLabels,numClasses,... filterDim,numFilters,poolDim,true); acc = sum(preds==testLabels)/length(preds); % Accuracy should be around 97.4% after 3 epochs fprintf('Accuracy is %f\n',acc);
cnnCost.m
function [cost, grad, preds] = cnnCost(theta,images,labels,numClasses,... filterDim,numFilters,poolDim,pred) % Calcualte cost and gradient for a single layer convolutional % neural network followed by a softmax layer with cross entropy % objective. % % Parameters: % theta - unrolled parameter vector % images - stores images in imageDim x imageDim x numImges % array % numClasses - number of classes to predict % filterDim - dimension of convolutional filter % numFilters - number of convolutional filters % poolDim - dimension of pooling area % pred - boolean only forward propagate and return % predictions % % % Returns: % cost - cross entropy cost % grad - gradient with respect to theta (if pred==False) % preds - list of predictions for each example (if pred==True) if ~exist('pred','var') pred = false; end; weightDecay = 0.0001; imageDim = size(images,1); % height/width of image numImages = size(images,3); % number of images %% Reshape parameters and setup gradient matrices % Wc is filterDim x filterDim x numFilters parameter matrix %convolution引數 % bc is the corresponding bias % Wd is numClasses x hiddenSize parameter matrix where hiddenSize % is the number of output units from the convolutional layer %這個convolutional layer應該是包含了卷積層和pool層 % bd is corresponding bias [Wc, Wd, bc, bd] = cnnParamsToStack(theta,imageDim,filterDim,numFilters,... poolDim,numClasses); % Same sizes as Wc,Wd,bc,bd. Used to hold gradient w.r.t above params. Wc_grad = zeros(size(Wc)); Wd_grad = zeros(size(Wd)); bc_grad = zeros(size(bc)); bd_grad = zeros(size(bd)); %%====================================================================== %% STEP 1a: Forward Propagation % In this step you will forward propagate the input through the % convolutional and subsampling (mean pooling) layers. You will then use % the responses from the convolution and pooling layer as the input to a % standard softmax layer. %% Convolutional Layer % For each image and each filter, convolve the image with the filter, add % the bias and apply the sigmoid nonlinearity. Then subsample the % convolved activations with mean pooling. Store the results of the % convolution in activations and the results of the pooling in % activationsPooled. You will need to save the convolved activations for % backpropagation. convDim = imageDim-filterDim+1; % dimension of convolved output outputDim = (convDim)/poolDim; % dimension of subsampled output % convDim x convDim x numFilters x numImages tensor for storing activations activations = zeros(convDim,convDim,numFilters,numImages); % outputDim x outputDim x numFilters x numImages tensor for storing % subsampled activations activationsPooled = zeros(outputDim,outputDim,numFilters,numImages); %%% YOUR CODE HERE %%% %呼叫之前寫的兩個函式 activations = cnnConvolve(filterDim, numFilters, images, Wc, bc); activationsPooled = cnnPool(poolDim, activations); % Reshape activations into 2-d matrix, hiddenSize x numImages, % for Softmax layer activationsPooled = reshape(activationsPooled,[],numImages);%就變成了傳統的softmax模式 %% Softmax Layer % Forward propagate the pooled activations calculated above into a % standard softmax layer. For your convenience we have reshaped % activationPooled into a hiddenSize x numImages matrix. Store the % results in probs. % numClasses x numImages for storing probability that each image belongs to % each class. probs = zeros(numClasses,numImages); %%% YOUR CODE HERE %%% z = Wd*activationsPooled; z = bsxfun(@plus,z,bd); %z = Wd * activationsPooled+repmat(bd,[1,numImages]); z = bsxfun(@minus,z,max(z,[],1));%減去最大值,減少一個維度,防止溢位 z = exp(z); probs = bsxfun(@rdivide,z,sum(z,1)); preds = probs; %%====================================================================== %% STEP 1b: Calculate Cost % In this step you will use the labels given as input and the probs % calculate above to evaluate the cross entropy objective. Store your % results in cost. cost = 0; % save objective into cost %%% YOUR CODE HERE %%% logProbs = log(probs); labelIndex=sub2ind(size(logProbs), labels', 1:size(logProbs,2)); %找出矩陣logProbs的線性索引,行由labels指定,列由1:size(logProbs,2)指定,生成線性索引返回給labelIndex values = logProbs(labelIndex); cost = -sum(values); weightDecayCost = (weightDecay/2) * (sum(Wd(:) .^ 2) + sum(Wc(:) .^ 2)); cost = cost / numImages+weightDecayCost; %Make sure to scale your gradients by the inverse size of the training set %if you included this scale in the cost calculation otherwise your code will not pass the numerical gradient check. % Makes predictions given probs and returns without backproagating errors. if pred [~,preds] = max(probs,[],1); preds = preds'; grad = 0; return; end; %%====================================================================== %% STEP 1c: Backpropagation % Backpropagate errors through the softmax and convolutional/subsampling % layers. Store the errors for the next step to calculate the gradient. % Backpropagating the error w.r.t the softmax layer is as usual. To % backpropagate through the pooling layer, you will need to upsample the % error with respect to the pooling layer for each filter and each image. % Use the kron function and a matrix of ones to do this upsampling % quickly. %%% YOUR CODE HERE %%% %softmax殘差 targetMatrix = zeros(size(probs)); targetMatrix(labelIndex) = 1; softmaxError = probs-targetMatrix; %pool層殘差 poolError = Wd'*softmaxError; poolError = reshape(poolError, outputDim, outputDim, numFilters, numImages); unpoolError = zeros(convDim, convDim, numFilters, numImages); unpoolingFilter = ones(poolDim); poolArea = poolDim*poolDim; %展開poolError為unpoolError for imageNum = 1:numImages for filterNum = 1:numFilters e = poolError(:, :, filterNum, imageNum); unpoolError(:, :, filterNum, imageNum) = kron(e, unpoolingFilter)./poolArea; end end convError = unpoolError .* activations .* (1 - activations); %%====================================================================== %% STEP 1d: Gradient Calculation % After backpropagating the errors above, we can use them to calculate the % gradient with respect to all the parameters. The gradient w.r.t the % softmax layer is calculated as usual. To calculate the gradient w.r.t. % a filter in the convolutional layer, convolve the backpropagated error % for that filter with each image and aggregate over images. %%% YOUR CODE HERE %%% %softmax梯度 Wd_grad = (1/numImages).*softmaxError * activationsPooled'+weightDecay * Wd; % l+1層殘差 * l層啟用值 bd_grad = (1/numImages).*sum(softmaxError, 2); % Gradient of the convolutional layer bc_grad = zeros(size(bc)); Wc_grad = zeros(size(Wc)); %計算bc_grad for filterNum = 1 : numFilters e = convError(:, :, filterNum, :); bc_grad(filterNum) = (1/numImages).*sum(e(:)); end %翻轉convError for filterNum = 1 : numFilters for imageNum = 1 : numImages e = convError(:, :, filterNum, imageNum); convError(:, :, filterNum, imageNum) = rot90(e, 2); end end for filterNum = 1 : numFilters Wc_gradFilter = zeros(size(Wc_grad, 1), size(Wc_grad, 2)); for imageNum = 1 : numImages Wc_gradFilter = Wc_gradFilter + conv2(images(:, :, imageNum), convError(:, :, filterNum, imageNum), 'valid'); end Wc_grad(:, :, filterNum) = (1/numImages).*Wc_gradFilter; end Wc_grad = Wc_grad + weightDecay * Wc; %% Unroll gradient into grad vector for minFunc grad = [Wc_grad(:) ; Wd_grad(:) ; bc_grad(:) ; bd_grad(:)]; end
cnnConvolve.m
function convolvedFeatures = cnnConvolve(filterDim, numFilters, images, W, b) %cnnConvolve Returns the convolution of the features given by W and b with %the given images % % Parameters: % filterDim - filter (feature) dimension % numFilters - number of feature maps % images - large images to convolve with, matrix in the form % images(r, c, image number) % W, b - W, b for features from the sparse autoencoder % W is of shape (filterDim,filterDim,numFilters) % b is of shape (numFilters,1) % % Returns: % convolvedFeatures - matrix of convolved features in the form % convolvedFeatures(imageRow, imageCol, featureNum, imageNum) numImages = size(images, 3); imageDim = size(images, 1); convDim = imageDim - filterDim + 1; convolvedFeatures = zeros(convDim, convDim, numFilters, numImages); % Instructions: % Convolve every filter with every image here to produce the % (imageDim - filterDim + 1) x (imageDim - filterDim + 1) x numFeatures x numImages % matrix convolvedFeatures, such that % convolvedFeatures(imageRow, imageCol, featureNum, imageNum) is the % value of the convolved featureNum feature for the imageNum image over % the region (imageRow, imageCol) to (imageRow + filterDim - 1, imageCol + filterDim - 1) % % Expected running times: % Convolving with 100 images should take less than 30 seconds % Convolving with 5000 images should take around 2 minutes % (So to save time when testing, you should convolve with less images, as % described earlier) for imageNum = 1:numImages for filterNum = 1:numFilters % convolution of image with feature matrix convolvedImage = zeros(convDim, convDim); % Obtain the feature (filterDim x filterDim) needed during the convolution %%% YOUR CODE HERE %%% filter = squeeze(W(:,:,filterNum)); % Flip the feature matrix because of the definition of convolution, as explained later filter = rot90(squeeze(filter),2); % Obtain the image im = squeeze(images(:, :, imageNum)); % Convolve "filter" with "im", adding the result to convolvedImage % be sure to do a 'valid' convolution %%% YOUR CODE HERE %%% convolvedImage = conv2(im,filter,'valid'); % Add the bias unit % Then, apply the sigmoid function to get the hidden activation %%% YOUR CODE HERE %%% convolvedImage = bsxfun(@plus,convolvedImage,b(filterNum)); convolvedImage = 1 ./ (1+exp(-convolvedImage)); convolvedFeatures(:, :, filterNum, imageNum) = convolvedImage; end end end
cnnPool.m
function pooledFeatures = cnnPool(poolDim, convolvedFeatures) %cnnPool Pools the given convolved features % % Parameters: % poolDim - dimension of pooling region % convolvedFeatures - convolved features to pool (as given by cnnConvolve) % convolvedFeatures(imageRow, imageCol, featureNum, imageNum) % % Returns: % pooledFeatures - matrix of pooled features in the form % pooledFeatures(poolRow, poolCol, featureNum, imageNum) % numImages = size(convolvedFeatures, 4); numFilters = size(convolvedFeatures, 3); convolvedDim = size(convolvedFeatures, 1); pooledFeatures = zeros(convolvedDim / poolDim, ... convolvedDim / poolDim, numFilters, numImages); % Instructions: % Now pool the convolved features in regions of poolDim x poolDim, % to obtain the % (convolvedDim/poolDim) x (convolvedDim/poolDim) x numFeatures x numImages % matrix pooledFeatures, such that % pooledFeatures(poolRow, poolCol, featureNum, imageNum) is the % value of the featureNum feature for the imageNum image pooled over the % corresponding (poolRow, poolCol) pooling region. % % Use mean pooling here. %%% YOUR CODE HERE %%% for imageNum = 1:numImages for featureNum = 1:numFilters featuremap = squeeze(convolvedFeatures(:,:,featureNum,imageNum)); pooledFeaturemap = conv2(featuremap,ones(poolDim)/(poolDim^2),'valid'); pooledFeatures(:,:,featureNum,imageNum) = pooledFeaturemap(1:poolDim:end,1:poolDim:end); end end end
computeNumericalGradient.m
function numgrad = computeNumericalGradient(J, theta) % numgrad = computeNumericalGradient(J, theta) % theta: a vector of parameters % J: a function that outputs a real-number. Calling y = J(theta) will return the % function value at theta. % Initialize numgrad with zeros numgrad = zeros(size(theta)); %% ---------- YOUR CODE HERE -------------------------------------- % Instructions: % Implement numerical gradient checking, and return the result in numgrad. % (See Section 2.3 of the lecture notes.) % You should write code so that numgrad(i) is (the numerical approximation to) the % partial derivative of J with respect to the i-th input argument, evaluated at theta. % I.e., numgrad(i) should be the (approximately) the partial derivative of J with % respect to theta(i). % % Hint: You will probably want to compute the elements of numgrad one at a time. epsilon = 1e-4; for i =1:length(numgrad) oldT = theta(i); theta(i)=oldT+epsilon; pos = J(theta); theta(i)=oldT-epsilon; neg = J(theta); numgrad(i) = (pos-neg)/(2*epsilon); theta(i)=oldT; if mod(i,100)==0 fprintf('Done with %d\n',i); end; end; %% --------------------------------------------------------------- end
minFuncSGD.m
function [opttheta] = minFuncSGD(funObj,theta,data,labels,... options) % Runs stochastic gradient descent with momentum to optimize the % parameters for the given objective. % % Parameters: % funObj - function handle which accepts as input theta, % data, labels and returns cost and gradient w.r.t % to theta. % theta - unrolled parameter vector % data - stores data in m x n x numExamples tensor % labels - corresponding labels in numExamples x 1 vector % options - struct to store specific options for optimization % % Returns: % opttheta - optimized parameter vector % % Options (* required) % epochs* - number of epochs through data % alpha* - initial learning rate % minibatch* - size of minibatch % momentum - momentum constant, defualts to 0.9 %%====================================================================== %% Setup assert(all(isfield(options,{'epochs','alpha','minibatch'})),... 'Some options not defined'); if ~isfield(options,'momentum') options.momentum = 0.9; end; epochs = options.epochs; alpha = options.alpha; minibatch = options.minibatch; m = length(labels); % training set size % Setup for momentum mom = 0.5; momIncrease = 20; velocity = zeros(size(theta)); %%====================================================================== %% SGD loop it = 0; for e = 1:epochs % randomly permute indices of data for quick minibatch sampling rp = randperm(m); for s=1:minibatch:(m-minibatch+1) it = it + 1; % increase momentum after momIncrease iterations if it == momIncrease mom = options.momentum; end; % get next randomly selected minibatch mb_data = data(:,:,rp(s:s+minibatch-1)); mb_labels = labels(rp(s:s+minibatch-1)); % evaluate the objective function on the next minibatch [cost grad] = funObj(theta,mb_data,mb_labels); % Instructions: Add in the weighted velocity vector to the % gradient evaluated above scaled by the learning rate. % Then update the current weights theta according to the % sgd update rule %%% YOUR CODE HERE %%% velocity = mom*velocity+alpha*grad; % 見ufldl教程Optimization: Stochastic Gradient Descent theta = theta-velocity; fprintf('Epoch %d: Cost on iteration %d is %f\n',e,it,cost); end; % aneal learning rate by factor of two after each epoch alpha = alpha/2.0; end; opttheta = theta; end
cnnInitParams.m
function theta = cnnInitParams(imageDim,filterDim,numFilters,... poolDim,numClasses) % Initialize parameters for a single layer convolutional neural % network followed by a softmax layer. % % Parameters: % imageDim - height/width of image % filterDim - dimension of convolutional filter % numFilters - number of convolutional filters % poolDim - dimension of pooling area % numClasses - number of classes to predict % % % Returns: % theta - unrolled parameter vector with initialized weights %% Initialize parameters randomly based on layer sizes. assert(filterDim < imageDim,'filterDim must be less that imageDim'); Wc = 1e-1*randn(filterDim,filterDim,numFilters); outDim = imageDim - filterDim + 1; % dimension of convolved image % assume outDim is multiple of poolDim assert(mod(outDim,poolDim)==0,... 'poolDim must divide imageDim - filterDim + 1'); outDim = outDim/poolDim; hiddenSize = outDim^2*numFilters; % we'll choose weights uniformly from the interval [-r, r] r = sqrt(6) / sqrt(numClasses+hiddenSize+1); Wd = rand(numClasses, hiddenSize) * 2 * r - r; bc = zeros(numFilters, 1); bd = zeros(numClasses, 1); % Convert weights and bias gradients to the vector form. % This step will "unroll" (flatten and concatenate together) all % your parameters into a vector, which can then be used with minFunc. theta = [Wc(:) ; Wd(:) ; bc(:) ; bd(:)]; end
cnnParamsToStack.m
function [Wc, Wd, bc, bd] = cnnParamsToStack(theta,imageDim,filterDim,... numFilters,poolDim,numClasses) % Converts unrolled parameters for a single layer convolutional neural % network followed by a softmax layer into structured weight % tensors/matrices and corresponding biases % % Parameters: % theta - unrolled parameter vectore % imageDim - height/width of image % filterDim - dimension of convolutional filter % numFilters - number of convolutional filters % poolDim - dimension of pooling area % numClasses - number of classes to predict % % % Returns: % Wc - filterDim x filterDim x numFilters parameter matrix % Wd - numClasses x hiddenSize parameter matrix, hiddenSize is % calculated as numFilters*((imageDim-filterDim+1)/poolDim)^2 % bc - bias for convolution layer of size numFilters x 1 % bd - bias for dense layer of size hiddenSize x 1 outDim = (imageDim - filterDim + 1)/poolDim; hiddenSize = outDim^2*numFilters; %% Reshape theta indS = 1; indE = filterDim^2*numFilters; Wc = reshape(theta(indS:indE),filterDim,filterDim,numFilters); indS = indE+1; indE = indE+hiddenSize*numClasses; Wd = reshape(theta(indS:indE),numClasses,hiddenSize); indS = indE+1; indE = indE+numFilters; bc = theta(indS:indE); bd = theta(indE+1:end); end
cnnExercise.m
%% Convolution and Pooling Exercise % Instructions % ------------ % % This file contains code that helps you get started on the % convolution and pooling exercise. In this exercise, you will only % need to modify cnnConvolve.m and cnnPool.m. You will not need to modify % this file. %%====================================================================== %% STEP 0: Initialization and Load Data % Here we initialize some parameters used for the exercise. imageDim = 28; % image dimension filterDim = 8; %相關推薦
Deep Learning 19_深度學習UFLDL教程:Convolutional Neural Network_Exercise(斯坦福大學深度學習教程)
基礎知識 概述 CNN是由一個或多個卷積層(其後常跟一個下采樣層)和一個或多個全連線層組成的多層神經網路。CNN的輸入是2維影象(或者其他2維輸入,如語音訊號)。它通過區域性連線和權值共享,再通過池化可得到平移不變特徵。CNN的另一個優點就是易於訓練
Deep Learning 1_深度學習UFLDL教程:Sparse Autoencoder練習(斯坦福大學深度學習教程)
1前言 本人寫技術部落格的目的,其實是感覺好多東西,很長一段時間不動就會忘記了,為了加深學習記憶以及方便以後可能忘記後能很快回憶起自己曾經學過的東西。 首先,在網上找了一些資料,看見介紹說UFLDL很不錯,很適合從基礎開始學習,Adrew Ng大牛寫得一點都不裝B,感覺非常好
Deep Learning 4_深度學習UFLDL教程:PCA in 2D_Exercise(斯坦福大學深度學習教程)
前言 本節練習的主要內容:PCA,PCA Whitening以及ZCA Whitening在2D資料上的使用,2D的資料集是45個數據點,每個資料點是2維的。要注意區別比較二維資料與二維影象的不同,特別是在程式碼中,可以看出主要二維資料的在PCA前的預處理不需要先0均值歸一化,而二維自然影象需要先
Deep Learning 11_深度學習UFLDL教程:資料預處理(斯坦福大學深度學習教程)
資料預處理是深度學習中非常重要的一步!如果說原始資料的獲得,是深度學習中最重要的一步,那麼獲得原始資料之後對它的預處理更是重要的一部分。 1.資料預處理的方法: ①資料歸一化: 簡單縮放:對資料的每一個維度的值進行重新調節,使其在 [0,1]或[ − 1,1] 的區間內 逐樣本均值消減:在每個
Deep Learning 13_深度學習UFLDL教程:Independent Component Analysis_Exercise(斯坦福大學深度學習教程)
前言 實驗環境:win7, matlab2015b,16G記憶體,2T機械硬碟 難點:本實驗難點在於執行時間比較長,跑一次都快一天了,並且我還要驗證各種代價函式的對錯,所以跑了很多次。 實驗基礎說明: ①不同點:本節實驗中的基是標準正交的,也是線性獨立的,而Deep Learni
Deep Learning 7_深度學習UFLDL教程:Self-Taught Learning_Exercise(斯坦福大學深度學習教程)
前言 理論知識:自我學習 練習環境:win7, matlab2015b,16G記憶體,2T硬碟 一是用29404個無標註資料unlabeledData(手寫數字資料庫MNIST Dataset中數字為5-9的資料)來訓練稀疏自動編碼器,得到其權重引數opttheta。這一步的目的是提取這
Deep Learning 2_深度學習UFLDL教程:向量化程式設計(斯坦福大學深度學習教程)
1前言 本節主要是讓人用向量化程式設計代替效率比較低的for迴圈。 在前一節的Sparse Autoencoder練習中已經實現了向量化程式設計,所以與前一節的區別只在於本節訓練集是用MINIST資料集,而上一節訓練集用的是從10張圖片中隨機選擇的8*8的10000張小圖塊。綜上,只需要在
Deep Learning 10_深度學習UFLDL教程:Convolution and Pooling_exercise(斯坦福大學深度學習教程)
前言 實驗環境:win7, matlab2015b,16G記憶體,2T機械硬碟 實驗內容:Exercise:Convolution and Pooling。從2000張64*64的RGB圖片(它是 the STL10 Dataset的一個子集)中提取特徵作為訓練資料集,訓練softmax分類器,然後從
Deep Learning 5_深度學習UFLDL教程:PCA and Whitening_Exercise(斯坦福大學深度學習教程)
close all; % clear all; %%================================================================ %% Step 0a: Load data % Here we provide the code to load n
Deep Learning 3_深度學習UFLDL教程:預處理之主成分分析與白化_總結(斯坦福大學深度學習教程)
1PCA ①PCA的作用:一是降維;二是可用於資料視覺化; 注意:降維的原因是因為原始資料太大,希望提高訓練速度但又不希望產生很大的誤差。 ② PCA的使用場合:一是希望提高訓練速度;二是記憶體太小;三是希望資料視覺化。 ③用PCA前的預處理:(1)規整化特徵的均值大致為0;(
Deep Learning 8_深度學習UFLDL教程:Stacked Autocoders and Implement deep networks for digit classification_Exercise(斯坦福大學深度學習教程)
前言 2.實驗環境:win7, matlab2015b,16G記憶體,2T硬碟 3.實驗內容:Exercise: Implement deep networks for digit classification。利用深度網路完成MNIST手寫數字資料庫中手寫數字的識別。即:用6萬個已標註資料(即:6萬
Deep Learning 12_深度學習UFLDL教程:Sparse Coding_exercise(斯坦福大學深度學習教程)
前言 實驗環境:win7, matlab2015b,16G記憶體,2T機械硬碟 本節實驗比較不好理解也不好做,我看很多人最後也沒得出好的結果,所以得花時間仔細理解才行。 實驗內容:Exercise:Sparse Coding。從10張512*512的已經白化後的灰度影象(即:Deep Learnin
Deep Learning 6_深度學習UFLDL教程:Softmax Regression_Exercise(斯坦福大學深度學習教程)
前言 練習內容:Exercise:Softmax Regression。完成MNIST手寫數字資料庫中手寫數字的識別,即:用6萬個已標註資料(即:6萬張28*28的影象塊(patches)),作訓練資料集,然後利用其訓練softmax分類器,再用1萬個已標註資料(即:1萬張28*28的影象塊(pa
Deep Learning 9_深度學習UFLDL教程:linear decoder_exercise(斯坦福大學深度學習教程)
前言 實驗基礎說明: 1.為什麼要用線性解碼器,而不用前面用過的棧式自編碼器等?即:線性解碼器的作用? 這一點,Ng已經在講解中說明了,因為線性解碼器不用要求輸入資料範圍一定為(0,1),而前面用過的棧式自編碼器等要求輸入資料範圍必須為(0,1)。因為a3的輸出值是f函式的輸出,而在普通的spa
實時翻譯的發動機:矢量語義(斯坦福大學課程解讀)
處理 多個 abi rod 進一步 ews 有一種 deb rac
Keras TensorFlow教程:如何從零開發一個複雜深度學習模型
Keras 是提供一些高可用的 Python API ,能幫助你快速的構建和訓練自己的深度學習模型,它的後端是 TensorFlow 或者 Theano 。本文假設你已經熟悉了 TensorFlow 和卷積神經網路,如果,你還沒有熟悉,那麼可以先看看這個10分鐘入門 TensorFlow 教程和卷積
斯坦福大學公開課機器學習:advice for applying machine learning | learning curves (改進學習算法:高偏差和高方差與學習曲線的關系)
繪制 學習曲線 pos 情況 但我 容量 繼續 並且 inf 繪制學習曲線非常有用,比如你想檢查你的學習算法,運行是否正常。或者你希望改進算法的表現或效果。那麽學習曲線就是一種很好的工具。學習曲線可以判斷某一個學習算法,是偏差、方差問題,或是二者皆有。 為了繪制一條學習曲
CS294-112深度增強學習課程(加州大學伯克利分校 2017)NO.3 Learning dynamical system models from data
增強 data learning http src img sys 增強學習 學習
《TensorFlow:實戰Google深度學習框架》——5.4 模型持久化(模型儲存、模型載入)
目錄 1、持久化程式碼實現 2、載入儲存的TensorFlow模型 3、載入部分變數 4、載入變數時重新命名 1、持久化程式碼實現 TensorFlow提供了一個非常簡單的API來儲存和還原一個神經網路模型。這個API就是tf.train.Saver類。一下程式碼給出了儲
斯坦福大學深度學習筆記:邏輯迴歸
z 邏輯迴歸(LOGISTIC REGRESSION) Logistic regression (邏輯迴歸)是當前業界比較常用的機器學習方法,用於估計某種事物的可能性。之前在經典之作《數學之美》中也看到了它用於廣告預測,也就是根據某廣告被使用者點選的可
