旋轉矩陣：

1.旋轉矩陣是正交矩陣，矩陣的每一行每一列的模，都為1；並且任意兩個列向量或者任意兩個行向量都是正交的。

2. 矩陣的行列式為1。矩陣的逆和轉置是相等的。

        什麼是旋轉矩陣？如圖1所示，我們假設最開始空間的座標系，，就是笛卡爾座標系，這樣我們得到空間A的矩陣={，，}T，其實也可以看做是單位陣E。進過旋轉後，空間A的三個座標系變成了圖1中紅色的三個座標系，，，得到空間B的矩陣={，，}T。我們將兩個空間聯絡起來可以得到=R•，這裡R就是我們所說的旋轉矩陣。

由於={1,0,0}T，={0,1,0}T，={0,0,1}T，結合圖2可以看出，旋轉矩陣R就是由，， 三個向量組成的(因為是單位陣)。因為單位向量無論怎麼旋轉長度肯定不會變而且向量之間的正交性質也不會變。那麼旋轉矩陣就是正交陣！如下式所示。

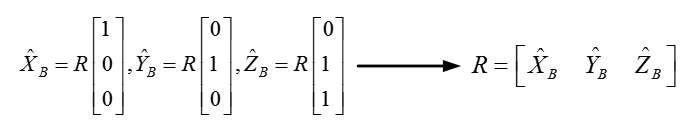
接下來就是重點了，我們結合圖4進行分析。由於旋轉矩陣R就是由，， 三個向量組成的。我們來看看，， 究竟是什麼？由於圖中所有的向量均是單位向量，所以與點乘的結果可以看成在上的投影的模，也就是在空間A中x軸的分量！！圖中中間的位置列出了向量中的三個分量分別為在上的投影的模、在上的投影的模和在上的投影的模。

       如圖6所示為例，由於繞x軸旋轉，所以我們觀察， 分別在和上的投影情況。旋轉矩陣的每一列表示旋轉後的單位向量方向，旋轉矩陣相當於把一個向量（空間）旋轉成新的向量（空間）

根據旋轉前後的向量求旋轉矩陣

1.旋轉角度

2.旋轉軸旋轉角所在的平面為有P和Q所構成的平面，那麼旋轉軸必垂直該平面。假定旋轉前向量為a

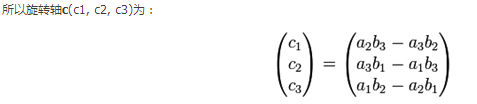
四元數

   四元數的一個最主要的應用就是表示旋轉，它既是緊湊的，也沒有奇異性。在講四元素之前，先來看下簡單的尤拉角和軸向角。

       尤拉角使用最簡單的x,y,z值來分別表示在x，y，z軸上的旋轉角度，其取值為0-360(或者0-2pi），一般使用roll，pitch，yaw來表示這些分量的旋轉值。需要注意的是，這裡的旋轉是針對世界座標系說的，這意味著第一次的旋轉不會影響第二、三次的轉軸。尤拉角容易出現的問題是 1）不易在任意方向的旋轉軸插值； 2）萬向節死鎖；3）旋轉的次序無法確定。

        軸角用一個以單位向量定義的旋轉角，再加上一個標量定義的旋轉角來表示旋轉。通常的表示[x,y,z,theta]，前面三個表示軸，最後一個表示角度。但是軸角形式的旋轉不能直接施於點或向量，必轉換為矩陣或者四元素。四元素感覺上就是軸角的進化，也是使用一個3維向量表示轉軸和一個角度分量表示繞此轉軸的旋轉角度，即(x,y,z,w)，觀察四維單位超球面在三維的投影，可以對它有個更深入的瞭解。（見文末連結）

 四元數：

1.一個四元數包含一個標量分量和一個3D向量分量。記標量為w，記向量為v或分開的x,y,z。如下：[w,v]即[w,(x,y,z)]。注意：單位四元素才能描述旋轉，所以四元素使用前必須歸一化：q.normalize()。

2.四元數擴充套件了複數系統 ，它使用三個虛部i,j,k。它們的關係如下：

ij=k,ji=-k；jk=i,kj=-i；ki=j,ik=-j

        一個四元數[w,(x,y,z)]定義了複數 w+xi+yj+zk。對於i、j、k本身的幾何意義可以理解為一種旋轉，其中i旋轉代表X軸與Y軸相交平面中X軸正向向Y軸正向的旋轉，j旋轉代表Z軸與X軸相交平面中Z軸正向向X軸正向的旋轉，k旋轉代表Y軸與Z軸相交平面中Y軸正向向Z軸正向的旋轉，-i、-j、-k分別代表i、j、k旋轉的反向旋轉

3.四元數和軸-角對：四元數能被解釋為角位移的軸-角對方式。設向量n為旋轉軸，θ為繞軸旋轉的量。

q=[cos(θ/2)  sin(θ/2)n]=[cos(θ/2)  (sin(θ/2)nx  sin(θ/2)ny  sin(θ/2)nz)]

（用一個旋轉軸n和旋轉角θ來描述一個旋轉，所以也稱軸角。不過很明顯，因為旋轉角度有一定的週期性（360°一圈），所以這種表達方式具有奇異性。從旋轉向量到旋轉矩陣的轉換過程稱為 羅德里格斯公式）

4.如何用四元數將3D點繞軸旋轉：

讓我們“擴充套件”一個標準3D點(x,y,z)到四元數空間，通過定義四元數p=[0, (x,y,z)]即可。設q為我們討論的旋轉四元數形式[cos(θ/2)  sin(θ/2)n]，n為旋轉軸單位向量，θ為旋轉角。執行下面乘法可使3D點p繞n旋轉：p'=qp.

       為什麼我們用 qp的方法表示三維旋轉，其中 p 是表示三維空間向量的純四元數。首先，如果待旋轉的向量 p 與單位四元數虛部所表示的旋轉軸正交時，我們只需要左乘單位四元數就可以表示此旋轉。如下圖所示，i 點繞 k 軸進行旋轉，左乘單位四元數 q 即可。可是對於大部分情況，向量 p 和旋轉軸並不正交，單單只是左乘單位四元數 q 會在三維空間中有拉伸的效果。注意整個三維空間都是單位超球面的投影，這裡的拉伸只不過是投影之後的一種效果罷了。我們用四元數並不關心四維單位超球面的旋轉，而是拿它來描述三維空間的旋轉，於是我們必須要找到一種不帶拉伸效果的四元數運算。人們發現，當右乘 q 的逆時，同方向的旋轉會繼續進行，而拉伸的效果互相抵消，於是就有了 qp. 的表示方法。

5.四元數的乘法和求逆

     乘法：給定兩個四元數p和q，分別代表旋轉P和Q，則乘積pq表示兩個旋轉的合成（即旋轉了Q之後再旋轉P）。四元數的乘法定義如下，利用簡單的分配律就是了：

q1 * q2 =(w1*w2 - x1*x2 - y1*y2 - z1*z2) +
(w1*x2 + x1*w2 + y1*z2 - z1*y2) i +(w1*y2 - x1*z2 + y1*w2 + z1*x2) j +(w1*z2 + x1*y2 - y1*x2 + z1*w2) k

由於q = w + x i + y j + z k中可以分為純量w與向量x i + y j + z k，所以為了方便表示，將q表示為(S, V)，其中S表示純量w，V表示向量x i + y j + z k，所以四元數乘法又可以表示為：

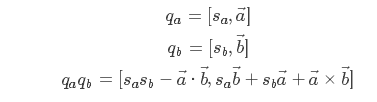
求逆：對於向量逆的定義, q-1 =q*/|q|2

對於單位四元素，分母為1，q-1 = q* =(-x, -y, -z, w)

6.四元素轉化為旋轉矩陣Matrix（3*3）：

1- 2*y*y - 2*z*z,  2x*y - 2*z*w,  2*x*z + 2y*w  

 2*x*y + 2*z*w, 1 - 2*x*x - 2*z*z, 2*y*z - 2*x*w

2*x*z - 2*y*w, 2*y*z + 2*x*w, 1 - 2*x*x - 2*y*y

補充：

四元數推導

對於一個複數p=a+bi，將它旋轉角度θ,先定義另外一個複數q=cosθ+isinθ,我們發現,複數的乘法表示了一種旋轉：

qp=(acosθ−bsinθ)+i(asinθ+bcosθ)。這個複數恰好就是p旋轉θ角度後的值。

看到了二維複數乘法可以表示旋轉，那麼三維空間呢，我們會想到再增加一個虛數作為第三個維度，我們定義兩個個三維的複數:

z1=a1+b1i+c1j，z2=a2+b2i+c2j

我們類似的進行復數的乘法,得到：

我們會發現,如果沒有ij和ji這兩項,我們三維的複數旋轉也就沒問題,那該如何處理呢，哈密爾頓引入四維的四數:q=q0+q1i+q2j+q3k,根據向量的叉乘可以定義下列一些關係（ij=-ji=k,是根據右手定則）：

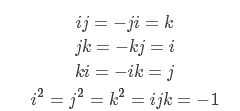
但是上面的旋轉是有缺點的,因為其限制了我們的旋轉軸和需要被旋轉的四元數必須是垂直的(a⃗ ⋅b⃗ =0a→⋅b→=0),而不能達到任意的旋轉.這時,聰明的哈密爾頓發現,一個四元數會把一個純四元數拉到四維空間,但它的共軛又會把這個四維的空間拉回到三維空間。

   

from：https://blog.csdn.net/qq_28773183/article/details/80083607 

from：http://www.cnblogs.com/caster99/p/4703033.html

from：http://www.zhuanzhi.ai/document/4d26b5d97249ca81129901ae7cd34a6c