1.KNN簡介

K近鄰(K-Nearest Neighbors, KNN)演算法既可處理分類問題，也可處理迴歸問題，其中分類和迴歸的主要區別在於最後做預測時的決策方式不同。KNN做分類預測時一般採用多數表決法，即訓練集裡和預測樣本特徵最近的K個樣本，預測結果為裡面有最多類別數的類別。KNN做迴歸預測時一般採用平均法，預測結果為最近的K個樣本資料的平均值。其中KNN分類方法的思想對迴歸方法同樣適用，因此本文主要講解KNN分類問題，下面我們通過一個簡單例子來了解下KNN演算法流程。

如下圖所示，我們想要知道綠色點要被決定賦予哪個類，是紅色三角形還是藍色正方形？我們利用KNN思想，如果假設K=3，選取三個距離最近的類別點，由於紅色三角形所佔比例為2/3，因此綠色點被賦予紅色三角形類別。如果假設K=5

1. 計算測試資料與各個訓練資料之間的距離。
2. 按照距離的遞增關係進行排序，選取距離最小的K個點。
3. 確定前K個點所在類別的出現頻率，返回前K個點中出現頻率最高的類別作為測試資料的預測分類。

從KNN演算法流程中，我們也能夠看出KNN演算法三個重要特徵，即距離度量方式、K值的選取和分類決策規則。

• 距離度量方式： KNN演算法常用歐式距離度量方式，當然我們也可以採用其他距離度量方式，比如曼哈頓距離，相應公式如下所示。

$D(x,y)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2+\mathrm{.}\mathrm{.}\mathrm{.}+(x_n-y_n}$

$D(x,y)={|x_1-y_1|+|x_2-y_2|+|x_3-y_3|...+|x_n-y_n|}={\sum_{i=1}^{n}|x_i-y_i|}$

• K值的選取： KNN演算法決策結果很大程度上取決於K值的選擇。選擇較小的K值相當於用較小領域中的訓練例項進行預測，訓練誤差會減小，但同時整體模型變得複雜，容易過擬合。選擇較大的K值相當於用較大領域中訓練例項進行預測，可以減小泛化誤差，但同時整體模型變得簡單，預測誤差會增大。
• 分類決策規則： KNN分類決策規則經常使用我們前面提到的多數表決法，在此不再贅述。

KNN要選取前K個最近的距離點，因此我們就要計算預測點與所有點之間的距離。但如果樣本點達到幾十萬，樣本特徵有上千，那麼KNN暴力計算距離的話，時間成本將會很高。因此暴力計算只適合少量樣本的簡單模型，那麼有沒有什麼方法適用於大樣本資料，有效降低距離計算成本呢？那是當然的，我們下面主要介紹KD樹和球樹方法。

2.KD樹原理

KD樹演算法沒有一開始就嘗試對測試樣本進行分類，而是先對訓練集建模，建立的模型就是KD樹，建立好模型之後再對測試集做預測。KD樹就是K個特徵維度的樹，注意KD樹中K和KNN中的K意思不同。KD樹中的K代表樣本特徵的維數，為了防止混淆，後面我們稱KD樹中特徵維數為n。KD樹可以有效減少最近鄰搜尋次數，主要分為建樹、搜尋最近鄰、預測步驟，下面我們對KD樹進行詳細講解。

2.1KD樹建立

下述為KD樹構建步驟，包括尋找劃分特徵、確定劃分點、確定左子空間和右子空間、遞迴構建KD樹。

1. 尋找劃分特徵： KD樹是從m個樣本的n維特徵中，分別計算n個特徵取值的方差，用方差最大的第k維特徵nk來作為根節點。
2. **確定劃分點：**選擇特徵nk的中位數nkv所對應的樣本作為劃分點。
3. **確定左子空間和右子空間：**對於所有第k維特徵取值小於nkv的樣本劃入左子樹，所有第k維特徵取值大於nkv的樣本劃入右子樹。
4. **遞迴構建KD樹：**對於左子樹和右子樹，採用和上述同樣的方法來找方差最大的特徵生成新節點，遞迴的構建KD樹。

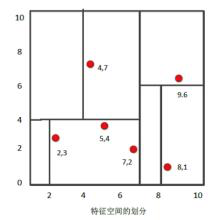
我們舉例來說明KD樹構建過程，假如有二維樣本6個，分別為{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}，KD樹過程構建過程如下

1. 尋找劃分特徵： 6個數據點在x,y維度上方差分別為6.97,5.37，x軸上方差更大，用第1維度特徵建樹。
2. **確定劃分點：**根據x維度上的值將資料排序，6個數據中x的中值為7，所以劃分點資料為(7,2)，該節點的分割超平面便是x=7直線。
3. **確定左子空間和右子空間：**分割超平面x=7將空間分為兩部分。x<=7的部分為左子空間，包含節點為{(2,3)，(5,4)，(4,7)}。x>7的部分為右子空間，包含節點為{(9,6)，(8,1)}。
4. **遞迴構建KD樹：**用同樣的方法劃分左子樹{(2,3)，(5,4)，(4,7)}和右子樹{(9,6)，(8,1)}，最終得到KD樹。
   
   

2.2KD樹搜尋最近鄰

當我們生成KD樹後，就可以預測測試樣本集裡面的樣本目標點。

1. 二叉搜尋：對於目標點，通過二叉搜尋，能夠很快在KD樹裡面找到包含目標點的葉子節點。
2. 回溯：為找到最近鄰，還需要進行回溯操作，演算法沿搜尋路徑反向查詢是否有距離查詢點更近的資料點。以目標點為圓心，目標點到葉子節點的距離為半徑，得到一個超球體，最鄰近點一定在這個超球體內部。
3. **更新最近鄰：**返回葉子節點的父節點，檢查另一葉子節點包含的超矩形體是否和超球體相交，如果相交就到這個子節點中尋找是否有更近的最近鄰，有的話就更新最近鄰。如果不相交就直接返回父節點的父節點，在另一子樹繼續搜尋最近鄰。當回溯到根節點時，演算法結束，此時儲存的最近鄰節點就是最終的最近鄰。

為方便理解上述過程，我們利用2.1建立的KD樹來尋找(2,4.5)的最近鄰。

1. **二叉搜尋：**首先從(7,2)節點查詢到(5,4)節點。由於目標點y=4.5，同時分割超平面為y=4，因此進入右子空間(4,7)進行查詢，形成搜尋路徑{(7,2)->(5,4)->(4,7)}。
2. **回溯：**節點(4,7)與目標查詢點距離為3.202，回溯到父節點(5,4)與目標查詢點之間距離為3.041，所以(5,4)為查詢點的最近鄰。以目標點(2,4.5)為圓心，以3.041為半徑作圓，最近鄰一定在超球體內部。
3. **更新最近鄰：**該圓和y = 4超平面交割，所以需要進入(5,4)左子空間進行查詢，將(2,3)節點加入搜尋路徑{(7,2)->(2,3)}。回溯至(2,3)葉子節點，(2,4.5)到(2,3)的距離比到(5,4)要近，所以最近鄰點更新為(2,3)，最近距離更新為1.5。回溯至(7,2)，以(2,4.5)為圓心，1.5為半徑作圓，發現並不和x = 7分割超平面交割，至此搜尋路徑回溯完成，完成更新最近鄰操作，返回最近鄰點(2,3)。

2.3KD樹預測

根據KD樹搜尋最近鄰的方法，我們能夠得到第一個最近鄰資料點，然後把它置為已選。然後忽略置為已選的樣本，重新選擇最近鄰，這樣執行K次，就能得到K個最近鄰。如果是KNN分類，根據多數表決法，預測結果為K個最近鄰類別中有最多類別數的類別。如果是KNN迴歸，根據平均法，預測結果為K個最近鄰樣本輸出的平均值。

3.球樹原理

KD樹演算法能夠提高KNN搜尋效率，但在某些時候效率並不高，比如處理不均勻分佈的資料集時。如下圖所示，如果黑色的例項點離目標點(星點)再遠一點，那麼虛線會像紅線那樣擴大，導致與左上方矩形的右下角相交。既然相交那就要檢查左上方矩形，而實際上最近的點離目標點(星點)很近，檢查左上方矩形區域已是多餘。因此KD樹把二維平面劃分成矩形會帶來無效搜尋的問題。

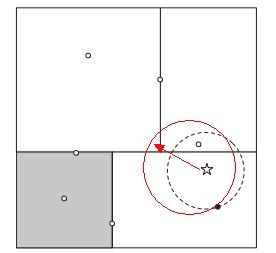
為優化超矩形體帶來的搜尋效率問題，我們在此介紹球樹演算法來進一步提高最近鄰搜尋效率。

3.1球樹建立

球樹的每個分割塊都是超球體，而不像KD樹中的超矩形體，這樣在做最近鄰搜尋是可以避免無效搜尋，下面我們介紹球樹構建過程

1. **構建超球體：**超球體是可以包含所有樣本的最小球體。
2. **劃分子超球體：**從超球體中選擇一個離超球體中心最遠的點，然後選擇第二個點離第一個點最遠，將球中所有的點分配到離這兩個聚類中心最近的一個。然後計算每個聚類的中心，以及聚類能夠包含它所有資料點所需的最小半徑，這樣我們便得到兩個子超球體，和KD樹中的左右子樹對應。
3. **遞迴：**對上述兩個子超球體，遞迴執行步驟2，最終得到球樹。
   

3.2球樹搜尋最近鄰

KD樹在搜尋路徑優化時使用的是兩點之間的距離來判斷，而球樹使用的是兩邊之和大於第三邊來判斷。相對來說球樹的判斷更加複雜，但卻避免一些無效的搜尋，下述為球樹搜尋最近鄰過程。

1. 自上而下貫穿整棵樹找出包含目標點所在的葉子，並在這個球裡找出與目標點最鄰近的點，這將確定目標點距離最鄰近點的上限值。
2. 然後和KD樹查詢相同，檢查兄弟結點，如果目標點到兄弟結點中心的距離超過兄弟結點的半徑與當前的上限值之和，那麼兄弟結點裡不可能存在一個更近的點。否則進一步檢查位於兄弟結點以下的子樹。
3. 檢查完兄弟節點後，向父節點回溯，繼續搜尋最小鄰近值。當回溯到根節點時，此時的最小鄰近值就是最終的搜尋結果。

3.3球樹預測

根據球樹搜尋最近鄰的方法，我們能夠得到第一個最近鄰資料點，然後把它置為已選。然後忽略置為已選的樣本，重新選擇最近鄰，這樣執行K次，就能得到K個最近鄰。如果是KNN分類，根據多數表決法，預測結果為K個最近鄰類別中有最多類別數的類別。如果是KNN迴歸，根據平均法，預測結果為K個最近鄰樣本輸出的平均值。

4.KNN演算法擴充套件

有時我們會遇到樣本中某個類別數的樣本非常少，甚至少於我們實現定義的K，這將導致稀有樣本在找K個最近鄰的時候會把距離較遠的無關樣本考慮進來，進而導致預測不準確。為解決此類問題，我們先設定最近鄰的一個最大距離，也就是說，我們在一定範圍內搜尋最近鄰，這個距離稱為限定半徑。

5.Sklearn實現KNN演算法

下述程式碼是利用iris資料進行分類，我們經常需要通過改變引數來讓模型達到分類結果，具體引數設定可參考sklearn官方教程。

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

#load iris data
iris=load_iris()
X=iris.data
y=iris.target
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=1)

knn=KNeighborsClassifier(algorithm='kd_tree')
knn.fit(X_train,y_train)
print(knn.predict(X_test))
# [0 1 1 0 2 1 2 0 0 2 1 0 2 1 1 0 1 1 0 0 1 1 1 0 2 1 0 0 1 2 1 2 1 2 2 0 1
#  0 1 2 2 0 1 2 1]
print(y_test)
# [0 1 1 0 2 1 2 0 0 2 1 0 2 1 1 0 1 1 0 0 1 1 1 0 2 1 0 0 1 2 1 2 1 2 2 0 1
#  0 1 2 2 0 2 2 1]
print(knn.score(X_test,y_test))
# 0.977777777778

6.KNN優缺點

6.1優點

• 即可處理分類也可處理迴歸問題。
• 對資料沒有假設，準確度高，對異常點不敏感。
• 比較適合樣本容量大的類域進行自動分類，對樣本容量較小的類域容易產生誤分。
• 主要靠周圍有限的鄰近樣本進行分類或迴歸，比較適合類域交叉或重疊較多的待分樣本集。

6.2缺點

• 計算量大，尤其是特徵維數較多時候。
• 樣本不平衡時，對稀有類別的預測準確率低。
• KD樹、球樹之類的模型建立時需要大量的記憶體。
• 使用懶惰學習方法，基本上不學習，導致預測時速度較慢。

7.推廣

更多內容請關注公眾號謂之小一，若有疑問可在公眾號後臺提問，隨時回答，歡迎關注，內容轉載請註明出處。

參考